codeforces 985 D. Sand Fortress(二分+思维）

Sand Fortress

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

You are going to the beach with the idea to build the greatest sand castle ever in your head! The beach is not as three-dimensional as you could have imagined, it can be decribed as a line of spots to pile up sand pillars. Spots are numbered 1 through infinity from left to right.

Obviously, there is not enough sand on the beach, so you brought n packs of sand with you. Let height hi of the sand pillar on some spot i be the number of sand packs you spent on it. You can't split a sand pack to multiple pillars, all the sand from it should go to a single one. There is a fence of height equal to the height of pillar with H sand packs to the left of the first spot and you should prevent sand from going over it.

Finally you ended up with the following conditions to building the castle:

• h1 ≤ H: no sand from the leftmost spot should go over the fence;
• For any 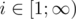 |hi - hi + 1| ≤ 1: large difference in heights of two neighboring pillars can lead sand to fall down from the higher one to the lower, you really don't want this to happen;
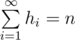• : you want to spend all the sand you brought with you.

As you have infinite spots to build, it is always possible to come up with some valid castle structure. Though you want the castle to be as compact as possible.

Your task is to calculate the minimum number of spots you can occupy so that all the aforementioned conditions hold.

Input

The only line contains two integer numbers n and H (1 ≤ n, H ≤ 1018) — the number of sand packs you have and the height of the fence, respectively.

Output

Print the minimum number of spots you can occupy so the all the castle building conditions hold.

Examples

input

5 2

output

3

input

6 8

output

3

Note

Here are the heights of some valid castles:

• n = 5, H = 2, [2, 2, 1, 0, ...], [2, 1, 1, 1, 0, ...], [1, 0, 1, 2, 1, 0, ...]
• n = 6, H = 8, [3, 2, 1, 0, ...], [2, 2, 1, 1, 0, ...], [0, 1, 0, 1, 2, 1, 1, 0...] (this one has 5spots occupied)

The first list for both cases is the optimal answer, 3 spots are occupied in them.

And here are some invalid ones:

• n = 5, H = 2, [3, 2, 0, ...], [2, 3, 0, ...], [1, 0, 2, 2, ...]
• n = 6, H = 8, [2, 2, 2, 0, ...], [6, 0, ...], [1, 4, 1, 0...], [2, 2, 1, 0, ...]

【题意】

对给定的nn,HH，把n划分为a1,a2，a3,...a1,a2，a3,...，要求首项a1≤Ha1≤H，相邻两项之差不大于1，而且最后一项必须是1。总个数要最少，输出这个最小的总个数。

【思路】

只求总个数，所以不必关心具体的序列。假设现在要分析总和为n，k个数的序列是否存在，就得去分解n，这件事是很难完成的，不如换一个角度，反向分析：所有满足“首项≤H≤H，相邻两项差不大于1，最后一项是1”的k个数的序列当中，有没有总和刚好是n的呢？

很容易发现 ，把kk定下来以后，一个满足条件的序列的总和，它的取值是一个连续的范围，而且下界明显是kk，那么上届是多少呢？

在kk个位置中填入最大的数，根据奇偶的不同，可能有下面两种情况，右边一定是黄色所示的三角形。如果n比较小可能只有黄色部分。

只要kk个数的和的区间[k,maxSUM][k,maxSUM]中包含nn，kk就是可行的。而且因为kk越大，maxSUM就越大，所以如果kk可行，那么k+1k+1也一定可行，正是因为这种单调性，可以kk进行二分查找。

【注意】

由于n, H比较i大，可能会出现乘积结果long long 溢出。为了避免在1~n进行二分，考虑一个更好的上届。我使用的下面的这种摆放的方法得到的上届：(k/2)2=n(k/2)2=n，所以最多用k=2√nk=2n个数

#include<stdio.h>
#include<math.h>
typedef long long ll;
ll n, H;
//绝对值
#define mabs(x) ((x)>0?(x):(0-(x)))//a, a+1, ...,b连续求和
#define SUM(a,b) (a+b)*(mabs(b-a)+1)/2
ll check(ll len)
{//检查三种情况，求maxSUM并于n比较
    ll area;
    if (len <= H)
        area = SUM(, len);
    else
    {
        area = SUM(, H-);
        len -= H;
        if (len & )
            area = area + SUM(H, H + len / ) + SUM(H + len / , H);
        else
            area = area + SUM(H, H + len / ) + SUM(H + len /  - , H);
    }
    return area >= n;
}

//二分查找k
ll binsch(ll fr,ll to)
{
    ll l = fr - , r = to + , m;
    while (l+<r)
    {
        m = (l + r) / ;
        if (check(m)!= )l = m;
        else r = m;
    }
    return r;
}

int main()
{
    scanf("%I64d %I64d", &n,&H);
    ll r = *sqrt(n)+;
    ll ans=binsch(, r);
    printf("%I64d", ans);
}