泉五培训Day1

T1 树学

题目

【问题描述】

给定一颗 n 个点的树，树边带权，试求一个排列 P，最大化下式

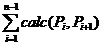
其中，calc(a, b)表示树上由a到b经过的最大边权。

【输入格式】

第一行一个整数 n，表示点数下接 n − 1 行，每行三个数 u, v, w 表示一条连接点 u 和点 v 权值为 w

【输出格式】

总共一行一个整数，表示答案

【输入样例】

2

1 2 2333

【输出样例】

2333

【数据范围】

对于前5%的数据满足 n ≤ 8

对于前40%的数据满足 n ≤ 20

对于前60%的数据满足 n ≤ 200

对于100%的数据满足 n ≤ 100

解析

先从边权最小的边开始累加，尽可能的减少当前边的贡献次数。发现每轮最少贡献一次，即将边两侧的点在P中完全分开。

试过多组数据之后，不难发现，答案即为所有边权之和。

1、最长边只计算过一次。

2、如果次长边被经过两次及以上，从次长边的一端出发，到了最长边的一端，走了一个来回，很显然，这是错误的，所以，次长边只计算过一次。

3、以此类推，最后，所有边都只计算过一次。

Code

#include <iostream>
#include <cstdio>
using namespace std;
int n,u,v,w;
long long ans;
int main()
{
    cin>>n;
    for(int i=;i<n;i++)
    {
        cin>>u>>v>>w;
        ans+=w;
    }
    cout<<ans;
    return ;
}

T2 保留道路

题目

【问题描述】

很久很久以前有一个国家，这个国家有N个城市，城市由1,2,3,…,N标号，城市间有M条双向道路，每条道路都有两个属性g和s，两个城市间可能有多条道路，并且可能存在将某一城市与其自身连接起来的道路。后来由于战争的原因，国王不得不下令减小花费从而关闭一些道路，但是必须要保证任意两个城市相互可达。

道路花费的计算公式为wG*max{所有剩下道路的属性g}+wS*max{所有剩下道路的属性s}，其中wG和wS是给定的值。国王想要在满足连通性的前提下使这个花费最小，现在需要你计算出这个花费。

【输入格式】

输入文件名为road.in。

第一行包含两个正整数N和M。

第二行包含两个正整数wG和wS。

后面的M行每行描述一条道路，包含四个正整数u,v,g,s，分别表示道路连接的两个城市以及道路的两个属性。

【输出格式】

输出文件名为road.out。

输出一个整数，表示最小花费。若无论如何不能满足连通性，输出-1。

【输入输出样例】

road.in	road.out
3 3 2 1 1 2 10 15 1 2 4 20 1 3 5 1	30

【数据规模与约定】

对于10%的数据，N≤10，M≤20；

对于30%的数据，N≤100，M≤1000；

对于50%的数据，N≤200，M≤5000；

对于100%的数据，N≤400，M≤50000，wG,wS,g,s≤1000000000。

解析

这题难在最小生成树有两个变量。

先按g从小到大排序，在加入边的过程中发现，当前的最小生成树只会由上一次的最小生成树和新边构成。

所以每次只需在N条边中生成最小生成树即可。

Code

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
#define INF 100000000000000000LL;
#define M 50010
#define N 410
long long ans=INF;
long long n,m,wS,wG,cnt,f[N];//cnt表示已生成的树的边数
struct rec{
    long long x,y;
    bool vis;//是否被使用过
    long long g,s;
}tree[M],small[M],ra[M];//tree表示初始数据，small表示最小生成树的数据，ra是最小生成树的替身
int find(long long x)
{
    if(f[x]==x) return x;
    return f[x]=find(f[x]);
}
bool cmp(rec a,rec b)
{
    if(a.g!=b.g) return a.g<b.g;
    else return a.s<b.s;
}
void kruskal(long long maxg)//生成最小生成树
{
    for(int i=;i<=cnt;i++)
    {
        ra[i]=small[i];//复制数据
        ra[i].vis=;//初始化,0为未访问 ,1为访问
    }
    long long maxs=,tot=;
    for(int i=;i<=n;i++)   f[i]=i; //并查集初始化
    for(int i=;i<=cnt;i++)
    {
        int a=find(small[i].x);
        int b=find(small[i].y);
        if(a!=b)
        {
            maxs=max(maxs,small[i].s);
            f[a]=b;
            tot++;
            ra[i].vis=;//标记
        }
        if(tot==n-)
        {
            int num=;
            for(int i=;i<=cnt;i++)
                if(ra[i].vis) small[++num]=ra[i];
            cnt=num;
            ans=min(ans,maxg+maxs);
            break;
        }
    }
}
void start()
{
    for(int i=;i<=m;i++)//按g的大小，从小到大枚举边
    {
        if(tree[i].g+tree[i].s>ans) continue;
        int pos=cnt+;
        for(int j=;j<=cnt;j++)
        {
            if(small[j].s>tree[i].s)
            {
                pos=j;
                break;
            }
        }
        if(pos==cnt+)
        {
            cnt++;
            small[cnt]=tree[i];
        }
        else
        {
           cnt++;
           for(int j=cnt;j>=pos+;j--) small[j]=small[j-];
           small[pos]=tree[i];
        }
        kruskal(tree[i].g);
     }
}
int main()
{
    cin>>n>>m>>wG>>wS;
    for(int i=;i<=m;i++)
    {
        cin>>tree[i].x>>tree[i].y>>tree[i].g>>tree[i].s;
        tree[i].g*=1LL*wG;
        tree[i].s*=1LL*wS;//初始化
    }
    sort(tree+,tree+m+,cmp);//将原数据的g从小到大排序
    start();
    cout<<ans;
    return ;
}

T3 appointment

题目

【问题描述】

定义两个排列v_i和g_i的“友好值”为：在1 <= i <= n中，出现v_i > g_i的次数。

给定n,m，以及一个1~n的排列v_i，你需要分别求出和排列v_i“友好值”为0，1，2，...，m的排列g_i有多少个。

【输入格式】

输入一共有两行。

第一行包含两个整数 n，m，意义如上

第二行包含 n 个整数，第 i 个为 vi，意义如上

【输出格式】

输出共 m+1 行，第i行友好值为 i-1 时的g_i有多少个。由于答案可能较大，请输出ans%998244353 的结果。

【样例输入】

3 2

1 3 2

【样例输出】

1

4

1

【样例解释】

友好值为0时，排列g只能是(1, 3, 2)

友好值为1时，排列g可以是(1, 2, 3)  (2, 1, 3)  (2, 3, 1)  (3, 1, 2)

友好值为2时，排列g只能是(3, 2, 1)

【数据范围】

对于20%的数据： n <= 10

对于100%的数据： n <= 6000

解析

先试几组数据，可以发现答案与v_i无关。

设f[i][j]表示当前序列长度为i时，友好值为j。

如果在原有序列中加入一个新数字，原有序列的友好值要么+1要么不变。

若友好值不变，则把新加入的数和一个具有贡献的数交换位置，共有(j+1)种换法。

若友好值+1，则把新加入的数和一个没有贡献的数交换位置，即(i-1)-(j-1)，即i-j。

于是得出了状态转移方程f[i][j]=f[i-1][j]*(j+1)+f[i-1][j-1]*(i-j)。

边界：f[i][0]=1。

Code

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
const long long mod=;
long long f[][];
int main()
{
    int n,m,temp;
    cin>>n>>m;
    for(int i=;i<=n;i++) cin>>temp;
    for(int i=;i<=n;i++) f[i][]=;
    for(int j=;j<=m;j++)
        for(int i=;i<=n;i++) f[i][j]=(f[i-][j]*(j+)%mod+f[i-][j-]*(i-j)%mod)%mod;
    for(int i=;i<=m;i++) cout<<f[n][i]<<endl;
    return ;
 }