洛谷-铺地毯-NOIP2011提高组复赛

题目描述

为了准备一个独特的颁奖典礼，组织者在会场的一片矩形区域（可看做是平面直角坐标系的第一象限）铺上一些矩形地毯。一共有 n 张地毯，编号从 1 到n 。现在将这些地毯按照编号从小到大的顺序平行于坐标轴先后铺设，后铺的地毯覆盖在前面已经铺好的地毯之上。

地毯铺设完成后，组织者想知道覆盖地面某个点的最上面的那张地毯的编号。注意：在矩形地毯边界和四个顶点上的点也算被地毯覆盖。

输入输出格式

输入格式：

输入文件名为carpet.in 。

输入共n+2 行。

第一行，一个整数n ，表示总共有 n 张地毯。

接下来的n 行中，第 i+1 行表示编号i 的地毯的信息，包含四个正整数 a ，b ，g ，k ，每两个整数之间用一个空格隔开，分别表示铺设地毯的左下角的坐标（a ，b ）以及地毯在x轴和y 轴方向的长度。

第n+2 行包含两个正整数 x 和y，表示所求的地面的点的坐标（x ，y）。

输出格式：

输出文件名为carpet.out 。

输出共1 行，一个整数，表示所求的地毯的编号；若此处没有被地毯覆盖则输出-1 。

输入输出样例

输入样例#1：

3
1 0 2 3
0 2 3 3
2 1 3 3
2 2

输出样例#1：

3

输入样例#2：

3
1 0 2 3
0 2 3 3
2 1 3 3
4 5

输出样例#2：

-1

说明

【样例解释1】

如下图，1 号地毯用实线表示，2 号地毯用虚线表示，3 号用双实线表示，覆盖点（2,2）的最上面一张地毯是 3 号地毯。

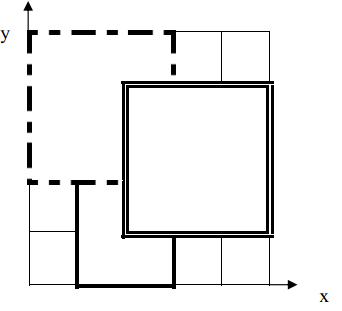
【数据范围】

对于30% 的数据，有 n ≤2 ；

对于50% 的数据，0 ≤a, b, g, k≤100；

对于100%的数据，有 0 ≤n ≤10,000 ，0≤a, b, g, k ≤100,000。

noip2011提高组day1第1题

思路：这题的数据十分的大，如果申请一个10000*10000的数组模拟肯定会超，所以必须寻找一个更加优化的方法

水题真的没多少讲的，代码里面有详细的注释。

代码如下：

 #include <stdio.h>
 #include <string.h>
 #include <math.h>
 int main()
 {
     int n,x,y;
     int i;
     int a[],b[],g[],k[];//(a,b)表示地毯左下角的坐标,g表示这个地毯在x轴上的长度,k表示这个地毯在y轴上的长度
     scanf("%d",&n);
     /*===========================*///对于这些数组全部清零
     memset(a,,sizeof(a));
     memset(b,,sizeof(b));
     memset(g,,sizeof(g));
     memset(k,,sizeof(k));
     /*===========================*/
     for(i=;i<n;i++)//分别输入到对应数组中
     {
         scanf("%d%d%d%d",&a[i],&b[i],&g[i],&k[i]);
     }
     scanf("%d%d",&x,&y);//输入要求的坐标
     for(i=n;i>=;i--)//从后往前找地毯（这样可以保证是最后一层）
     {
         if(a[i]<=x&&b[i]<=y)
         {
             if((a[i]+g[i])>=x&&(b[i]+k[i])>=y)
             {
                 printf("%d\n",i+);//找到了就输出并返回,由于是从后往前找的，肯定是最后一层
                 return ;
             }
         }
     }
     printf("-1\n");//经过这一番寻找没有找到就输出-1
     return ;
 }