【Soft-Margin Support Vector Machine】林轩田机器学习技术

Hard-Margin的约束太强了：要求必须把所有点都分开。这样就可能带来overfiiting，把noise也当成正确的样本点了。

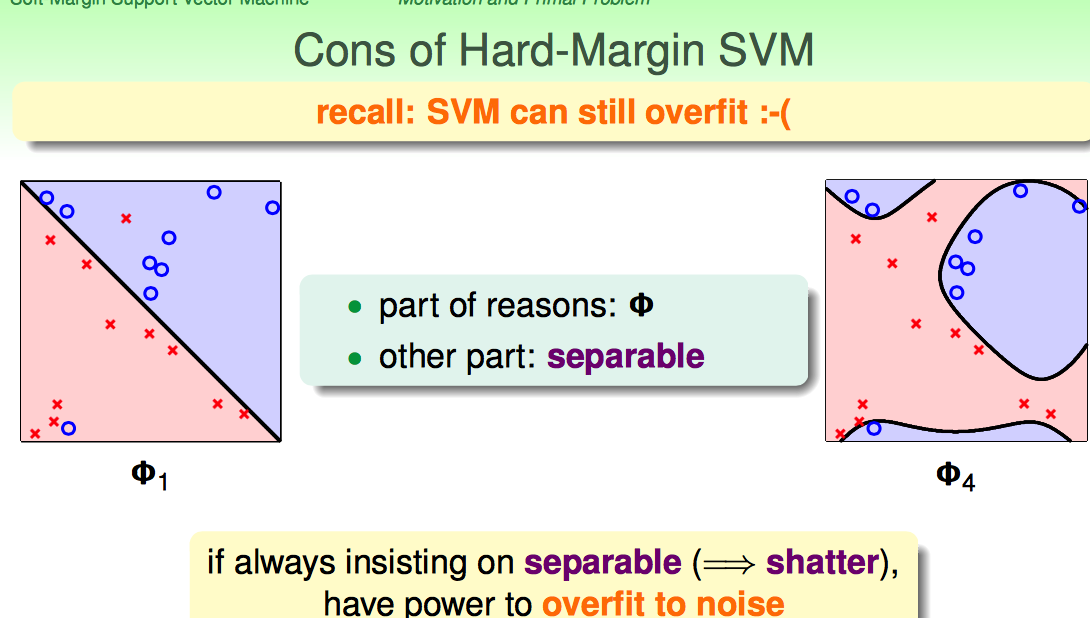
Hard-Margin有些“学习洁癖”，如何克服这种学习洁癖呢？

沿用pocket算法的思想，修改一下优化目标函数的形式，补上一个错分点的惩罚项CΣ...。

（1）C越大，对错误的容忍度就越小，margin越小

（2）C越小，对错误容忍度就越高，margin越大

因此引入的参数C是在large margin和noise tolerance之间做了一个权衡。

但是上面这种形式，有两个弊端：

（1）由于需要判断“等与不等”，所以是NP-hard Solution

（2）无法区分犯错点的错误程度

因此，引出了soft-margin的改进：

引入一个新的松弛因子kesi：

（1）既能解决学习洁癖的问题

（2）又能表示violation的程度是多少（kesi小于1还是分队的点，只不过此时点还在margin与hyperplane中间；kesi大于1表示分错了，越到hyperplance的另一端去了）

（3）还能转化成标准的QP问题，易于求解

接下来，沿用hard-margin dual svm的思路，把soft-margin SVM primal → dual。

由于不等式约束条件变成了两类，所以自然引入两个Largrange乘子；再沿用hard-margin的转化思路，转化成dual问题求解。

首先对kesi进行求导，化简原优化目标函数：

结论：

（1）利用对kesi求导为0的条件，把beta和kesi都去掉

（2）增加一个对alpha的约束条件

再进行接下来的化简，最终形式跟hard-margin很像。

不同之处在于对alpha增加了一个上界的约束条件。

一切看起来都比较顺利，但是在优化完成后，我们需要求解W和b。

W好求（alphan!=0的点，就可以作为支撑向量），问题的关键是b怎么求。

这里需要回顾KKT中的complementary slackness条件。

这里林直接给出来了，要free的那些SV（即满足kesi=0）来求解b；即对b求解有帮助的点，是真正在margin边界上的SV。

如果对之前SVM的complementary slackness内容不是很熟练，这块容易理解不好：为啥要分三类呢？

在这里，我重新理解了一下complementary slackness的意义。

意义就是，dual problem求出的最优解，带入原问题必须能使得Lagrange disappear。

由dual problem的推导可知，最优解的一个约束就是0<=alpha<=C，所以可以按照alpha取值分三种情况讨论。

（1）当alphan=0的时候：kesin=0，此时yn(W'xn+b)>=1-kesin必然成立（如果不成立，肯定不能作为最优解了）；

　　　　此时，要么在margin的边界上（取等）；更多的情况是yn(W'xn+b)>1（远离边界的点）

（2）当0<alphan<C的时候：kesin=0，并且yn(W'xn+b)=1-kesin=1，这两个等式都要成立；

　　　　显然，这时候就是满足条件的SV所在

（3）当alphan=C的时候：kesin可以不为零，但yn(W'xn+b)=1-kesin一定成立；

　　　　（3.a）这些点还是分对了，kesin小于1，只不过处于最大margin的内部

　　　　（3.b）这些点分错了，kesin大于1，已经越到hyperplane的另一侧了

对比hard-margin SVM问题：

之前min的目标函数是1/2W’W，但不要忘记了，之所以敢把min的目标函数写成1/2W'W的条件，是有yn(W'xn+b)>=1来保证的。

现在支撑向量依然是yn(W'xn+b)=1（绝大多数情况都有支撑向量，少数情况没有支撑向量），但是允许有一些向量可以yn(W'xn+b)<1；至于小多少，则要靠kesin来确定。

回想linear SVM的求解过程：alphan=0的点 都是SV candidates，但是不一定是SV

再联系Soft-Margin SVM的求解过程：alhphan=0的点同样要排除，因为仅仅是candidates; 但同时又多了一个约束alphan=C的时候，kesin可以不是0，kesin也可以是0，因此也仅仅能作为free SV的candidate；为了排除这两部分的candidates，掐头去尾，只取0<kesin<C的点作为free SV。

直观上松弛因子是怎么作用的？想象下面的一种情况：

输入数据是下图：

　

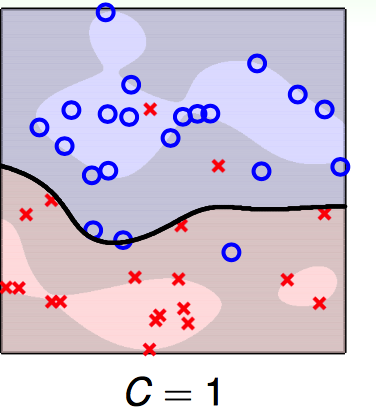
需要优化的目标函数和约束条件如下：

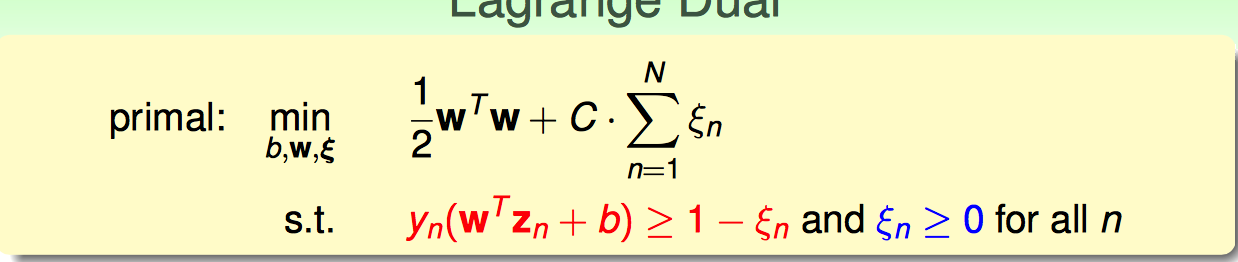
现在考虑处理hidden在圈圈中的那个红叉给分对，面临的情况是这样的：

（1）如果把其分对，则1/2W'W会增大不少（比如0<kesin<1，如果将其分对了，则就跟hard-margin SVM一样了；即yn(Wnew'xn+b)>=1，这里的Wnew = W/1-kesin；显然1/2W’W增加了，而如果这个增加的幅度大于Ckesin，则优化过程就会选择将其分错，以保证primal的问题最优）

（2）如果把其分错且认了，错就错了，则多付出的代价是C*kesin

这时候就要权衡让1/2W'W增大的与分错付出的代价C*kesin哪个大了？

如果是下面两种情况：

由于C取得很大，所以分错的代价太大了，1/2W‘W与其比起来太弱了；因此就倾向于将所有的点都分对；于是overfitting了。

实际中，要适当选取各种参数。

一般来说，如果支撑向量的个数太多了，都存在过拟合的风险。