Luogu 2668 [NOIP2015]斗地主

打牌技术不精，没有把$A$放在顺子里面搜，WA了好长时间。

盗用大佬的一张图：

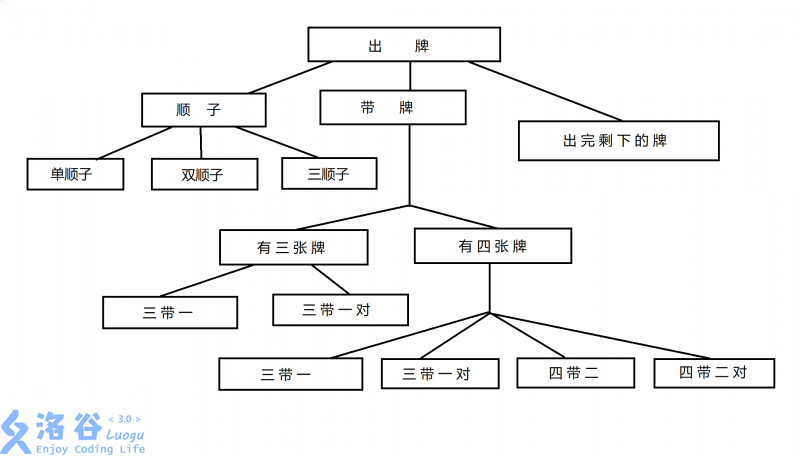
当时自己搜的时候没有把四张牌拆成三带一等情况。

然后还有一点就是四张三张都出完之后直接数一数剩下的一张两张牌还要多少次出完就好了，没有必要浪费栈空间和递归深度去搜这些东西。（我就是这样T了好多次QωQ）。

要注意暴力算的前提就是一定要把之前的三张四张打完。

玄学复杂度。

代码很丑很长。

Code：

#include <cstdio>
#include <cstring>
using namespace std;

const int N = ;
const int inf =  << ;

int testCase, n, cnt[N], ans;

inline void read(int &X) {
    X = ; char ch = ; int op = ;
    for(; ch > '' || ch < ''; ch = getchar())
        if(ch == '-') op = -;
    for(; ch >= '' && ch <= ''; ch = getchar())
        X = (X << ) + (X << ) + ch - ;
    X *= op;
}

inline void chkMin(int &x, int y) {
    if(y < x) x = y;
}

void dfs(int rest, int stp) {
    if(stp >= ans) return;
    if(rest == ) {
        chkMin(ans, stp);
        return;
    }

/*    for(int j, i = 3; i <= 14; i++) {
        if(cnt[i] < 1) continue;
        for(j = i; j <= 14; j++)
            if(cnt[j] < 1) break;
        j--;
        if(j - i + 1 < 5) {
            i = j;
            continue;
        }
        for(int k = i; k <= j; k++) --cnt[k];
        dfs(rest - (j - i + 1), stp + 1);
        for(int k = i; k <= j; k++) ++cnt[k];
        i = j;
    }    

    for(int j, i = 3; i <= 14; i++) {
        if(cnt[i] < 2) continue;
        for(j = i; j <= 14; j++)
            if(cnt[j] < 2) break;
        j--;
        if(j - i + 1 < 3) {
            i = j;
            continue;
        }
        for(int k = i; k <= j; k++) cnt[k] -= 2;
        dfs(rest - (j - i + 1) * 2, stp + 1);
        for(int k = i; k <= j; k++) cnt[k] += 2;
        i = j;
    }

    for(int j, i = 3; i <= 14; i++) {
        if(cnt[i] < 3) continue;
        for(j = i; j <= 14; j++)
            if(cnt[j] < 3) break;
        j--;
        if(j - i + 1 < 2) {
            i = j;
            continue;
        }
        for(int k = i; k <= j; k++) cnt[k] -= 3;
        dfs(rest - (j - i + 1) * 3, stp + 1);
        for(int k = i; k <= j; k++) cnt[k] += 3;
        i = j;
    }  */

/*    for(int j, k, i = 2; i <= 14; i++) {
        if(cnt[i] < 4) continue;
        for(j = 2; j <= 15; j++) {
            if(j == i) continue;
            if(cnt[j] > 1) {
                for(k = 2; k <= 15; k++) {
                    if(k == i) continue;
                    if(cnt[k] > 1) {
                        cnt[i] -= 4, cnt[j] -= 2, cnt[k] -= 2;
                        dfs(rest - 8, stp + 1);
                        cnt[i] += 4, cnt[j] += 2, cnt[k] += 2;
                    }
                }
            }
        }
    }

    for(int j, k, i = 2; i <= 14; i++) {
        if(cnt[i] < 4) continue;
        for(j = 2; j <= 15; j++) {
            if(j == i) continue;
            if(cnt[j] > 0) {
                for(k = 2; k <= 15; k++) {
                    if(k == i) continue;
                    if(cnt[k] > 0) {
                        cnt[i] -= 4, --cnt[j], --cnt[k];
                        dfs(rest - 6, stp + 1);
                        cnt[i] += 4, ++cnt[j], ++cnt[k];
                    }
                }
            }
        }
    }

    for(int i = 2; i <= 14; i++) {
        if(cnt[i] < 4) continue;
        cnt[i] -= 4;
        dfs(rest - 4, stp + 1);
        cnt[i] += 4;
    }

    for(int j, i = 2; i <= 14; i++) {
        if(cnt[i] < 3) continue;
        for(j = 2; j <= 15; j++) {
            if(j == i) continue;
            if(cnt[j] > 1) {
                cnt[i] -= 3, cnt[j] -= 2;
                dfs(rest - 5, stp + 1);
                cnt[i] += 3, cnt[j] += 2;
            }
        }
    }

    for(int j, i = 2; i <= 14; i++) {
        if(cnt[i] < 3) continue;
        for(j = 2; j <= 15; j++) {
            if(j == i) continue;
            if(cnt[j] > 0) {
                cnt[i] -= 3, --cnt[j];
                dfs(rest - 4, stp + 1);
                cnt[i] += 3, ++cnt[j];
            }
        }
    }

    for(int i = 2; i <= 14; i++) {
        if(cnt[i] < 3) continue;
        cnt[i] -= 3;
        dfs(rest - 3, stp + 1);
        cnt[i] += 3;
    }   */

    int len = ;
    for(int i = ; i <= ; i++) {
        if(cnt[i] == ) len = ;
        else {
            ++len;
            if(len >= ) {
                for(int j = i; j >= i - len + ; j--) cnt[j]--;
                dfs(rest - len, stp + );
                for(int j = i; j >= i - len + ; j--) cnt[j]++;
            }
        }
    }

    len = ;
    for(int i = ; i <= ; i++) {
        if(cnt[i] <= ) len = ;
        else {
            ++len;
            if(len >= ) {
                for(int j = i; j >= i - len + ; j--) cnt[j] -= ;
                dfs(rest - len * , stp + );
                for(int j = i; j >= i - len + ; j--) cnt[j] += ;
            }
        }
    }

    len = ;
    for(int i = ; i <= ; i++) {
        if(cnt[i] <= ) len = ;
        else {
            len++;
            if(len >= ) {
                for(int j = i; j >= i - len + ; j--) cnt[j] -= ;
                dfs(rest - len * , stp + );
                for(int j = i; j >= i - len + ; j--) cnt[j] += ;
            }
        }
    }

    for(int i = ; i <= ; i++) {
        if(cnt[i] <= ) {
            if(cnt[i] <= ) continue;
            cnt[i] -= ;
            for(int j = ; j <= ; j++) {
                if(j == i || cnt[j] == ) continue;
                cnt[j]--;
                dfs(rest - , stp + );
                cnt[j]++;
            }
            for(int j = ; j <= ; j++) {
                if(j == i || cnt[j] <= ) continue;
                cnt[j] -= ;
                dfs(rest - , stp + );
                cnt[j] += ;
            }
            cnt[i] += ;
        } else {
            cnt[i] -= ;
            for(int j = ; j <= ; j++) {
                if(j == i || cnt[j] == ) continue;
                cnt[j]--;
                dfs(rest - , stp + );
                cnt[j]++;
            }
            for(int j = ; j <= ; j++) {
                if(j == i || cnt[j] <= ) continue;
                cnt[j] -= ;
                dfs(rest - , stp + );
                cnt[j] += ;
            }
            cnt[i] += ;

            cnt[i] -= ;
            for(int j = ; j <= ; j++) {
                if(j == i || cnt[j] == ) continue;
                cnt[j]--;
                for(int k = ; k <= ; k++) {
                    if(k == j || cnt[k] == ) continue;
                    cnt[k]--;
                    dfs(rest - , stp + );
                    cnt[k]++;
                }
                cnt[j]++;
            }

            for(int j = ; j <= ; j++) {
                if(j == i || cnt[j] <= ) continue;
                cnt[j] -= ;
                for(int k = ; k <= ; k++) {
                    if(k == j || cnt[k] <= ) continue;
                    cnt[k] -= ;
                    dfs(rest - , stp + );
                    cnt[k] += ;
                }
                cnt[j] += ;
            }
            cnt[i] += ;
        }
    }

    int now = ;
    for(int i = ; i <= ; i++)
        if(cnt[i]) ++now;

    chkMin(ans, stp + now);
}

int main() {
//    freopen("Sample.txt", "r", stdin);
//    freopen("testdata.in", "r", stdin);
//    freopen("my.txt", "w", stdout);

    read(testCase), read(n);
    for(; testCase--; ) {
        memset(cnt, , sizeof(cnt));

        for(int x, y, i = ; i <= n; i++) {
            read(x), read(y);
            if(x == ) cnt[]++;
            else {
                if(x == ) cnt[]++;
                else cnt[x]++;
            }
        }

        ans = inf;
        dfs(n, );

        printf("%d\n", ans);
    }
    return ;
}