CF431C k-Tree dp

Quite recently a creative student Lesha had a lecture on trees. After the lecture Lesha was inspired and came up with the tree of his own which he called a k-tree.

A k-tree is an infinite rooted tree where:

• each vertex has exactly k children;
• each edge has some weight;
• if we look at the edges that goes from some vertex to its children (exactly k edges), then their weights will equal 1, 2, 3, ..., k.

The picture below shows a part of a 3-tree.

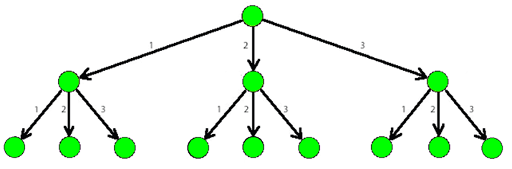
As soon as Dima, a good friend of Lesha, found out about the tree, he immediately wondered: "How many paths of total weight n (the sum of all weights of the edges in the path) are there, starting from the root of a k-tree and also containing at least one edge of weight at least d?".

Help Dima find an answer to his question. As the number of ways can be rather large, print it modulo 1000000007 (10⁹ + 7).

Input

A single line contains three space-separated integers: n, k and d (1 ≤ n, k ≤ 100; 1 ≤ d ≤ k).

Output

Print a single integer — the answer to the problem modulo 1000000007 (10⁹ + 7).

Examples

Input

Copy

3 3 2

Output

Copy

3

Input

Copy

3 3 3

Output

Copy

1

Input

Copy

4 3 2

Output

Copy

6

Input

Copy

4 5 2

Output

Copy

7

题目描述

最近有一个富有创造力的学生Lesha听了一个关于树的讲座。在听完讲座之后，Lesha受到了启发，并且他有一个关于k-tree（k叉树）的想法。 k-tree都是无根树，并且满足：

1. 每一个非叶子节点都有k个孩子节点；
2. 每一条边都有一个边权；
3. 每一个非叶子节点指向其k个孩子节点的k条边的权值分别为1,2,3,...,k。

---

当Lesha的好朋友Dima看到这种树时，Dima马上想到了一个问题：“有多少条从k-tree的根节点出发的路上的边权之和等于n，并且经过的这些边中至少有一条边的边权大于等于d呢?” 现在你需要帮助Dima解决这个问题。考虑到路径总数可能会非常大，所以只需输出路径总数 mod 1000000007 即可。（1000000007=10^9+7）

考虑dp[ i ][ 1/0 ]表示总和为i时，最大值是否>=d的方案数；

然后枚举中间状态转移；

注意long long ；

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstdlib>
#include<cstring>
#include<string>
#include<cmath>
#include<map>
#include<set>
#include<vector>
#include<queue>
#include<bitset>
#include<ctime>
#include<deque>
#include<stack>
#include<functional>
#include<sstream>

//#include<cctype>
//#pragma GCC optimize("O3")
using namespace std;
#define maxn 1000005
#define inf 0x3f3f3f3f
#define INF 9999999999
#define rdint(x) scanf("%d",&x)
#define rdllt(x) scanf("%lld",&x)
#define rdult(x) scanf("%lu",&x)
#define rdlf(x) scanf("%lf",&x)
#define rdstr(x) scanf("%s",x)
typedef long long  ll;
typedef unsigned long long ull;
typedef unsigned int U;
#define ms(x) memset((x),0,sizeof(x))
const long long int mod = 1e9 + 7;
#define Mod 1000000000
#define sq(x) (x)*(x)
#define eps 1e-3
typedef pair<int, int> pii;
#define pi acos(-1.0)
//const int N = 1005;
#define REP(i,n) for(int i=0;i<(n);i++)

inline ll rd() {
	ll x = 0;
	char c = getchar();
	bool f = false;
	while (!isdigit(c)) {
		if (c == '-') f = true;
		c = getchar();
	}
	while (isdigit(c)) {
		x = (x << 1) + (x << 3) + (c ^ 48);
		c = getchar();
	}
	return f ? -x : x;
}

ll gcd(ll a, ll b) {
	return b == 0 ? a : gcd(b, a%b);
}
ll sqr(ll x) { return x * x; }

/*ll ans;
ll exgcd(ll a, ll b, ll &x, ll &y) {
	if (!b) {
		x = 1; y = 0; return a;
	}
	ans = exgcd(b, a%b, x, y);
	ll t = x; x = y; y = t - a / b * y;
	return ans;
}
*/

ll qpow(ll a, ll b, ll c) {
	ll ans = 1;
	a = a % c;
	while (b) {
		if (b % 2)ans = ans * a%c;
		b /= 2; a = a * a%c;
	}
	return ans;
}
/*
int n, m;
int st, ed;
struct node {
	int u, v, nxt, w;
}edge[maxn<<1];

int head[maxn], cnt;

void addedge(int u, int v, int w) {
	edge[cnt].u = u; edge[cnt].v = v; edge[cnt].w = w;
	edge[cnt].nxt = head[u]; head[u] = cnt++;
}

int rk[maxn];

int bfs() {
	queue<int>q;
	ms(rk);
	rk[st] = 1; q.push(st);
	while (!q.empty()) {
		int tmp = q.front(); q.pop();
		for (int i = head[tmp]; i != -1; i = edge[i].nxt) {
			int to = edge[i].v;
			if (rk[to] || edge[i].w <= 0)continue;
			rk[to] = rk[tmp] + 1; q.push(to);
		}
	}
	return rk[ed];
}
int dfs(int u, int flow) {
	if (u == ed)return flow;
	int add = 0;
	for (int i = head[u]; i != -1 && add < flow; i = edge[i].nxt) {
		int v = edge[i].v;
		if (rk[v] != rk[u] + 1 || !edge[i].w)continue;
		int tmpadd = dfs(v, min(edge[i].w, flow - add));
		if (!tmpadd) { rk[v] = -1; continue; }
		edge[i].w -= tmpadd; edge[i ^ 1].w += tmpadd; add += tmpadd;
	}
	return add;
}
ll ans;
void dinic() {
	while (bfs())ans += dfs(st, inf);
}
*/

int n, k, d;
ll dp[200][2];

int main()
{
	//ios::sync_with_stdio(0);
	//memset(head, -1, sizeof(head));
	while (cin >> n >> k >> d) {
		ms(dp); dp[0][0] = 1;
		for (int i = 1; i <= n; i++) {
			for (int j = 1; j <= k; j++) {
				if (i >= j) {
					if (j < d) {
						dp[i][0] = (dp[i][0] + dp[i - j][0]) % mod;
						dp[i][1] = (dp[i][1] + dp[i - j][1]) % mod;
					}
					else {
						dp[i][1] = (dp[i][1] + dp[i - j][0] + dp[i - j][1]) % mod;
					}
				}
			}
		}
		cout << (ll)dp[n][1] << endl;
	}
    return 0;
}