吴恩达机器学习笔记（四） —— BP神经网络

主要内容：

一.模型简介

二.一些变量所代表的含义

三.代价函数

四.Forward Propagation

五.Back Propagation

六.算法流程

待解决问题：

视频中通过指出：当特征变多时（或者非线性），利用logistic回归模型解决问题将导致计算量很大，即算法复杂度很高。然后就此引出神经网路，所以说神经网路在解决多特征（或者非线性）问题上是比logistic回归更优的。但为什么呢？有什么合理的解释？

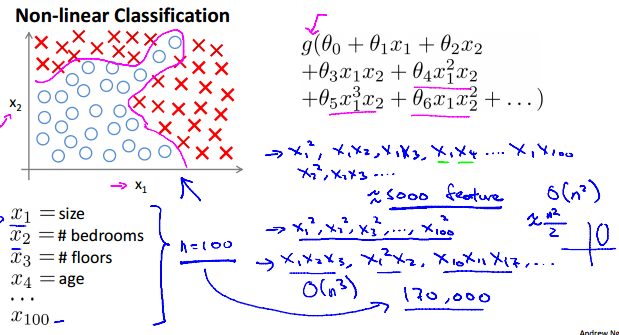
一.模型简介

1.最简单的神经网络就是只有输入层和输出层：

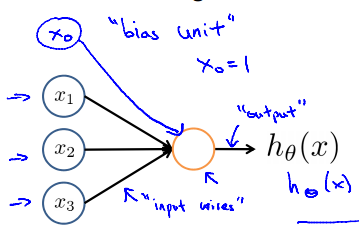
2.稍微复杂一点（中间的被称为隐藏层）：

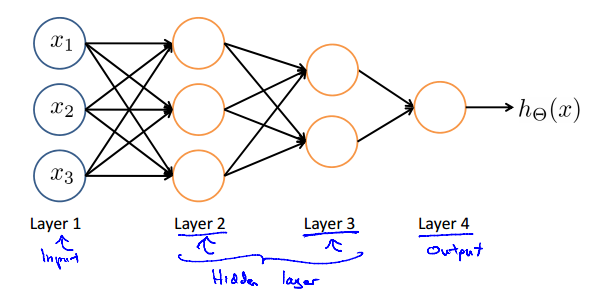
3.其中，当前层的输出作为下一层每一个结点的输入（的一部分），即n*m的全相连，且每一条边都带有权重，就是说我们要训练的参数。

4.在每一层当中，除了我们预先设定的结点之外，还在最上面添加一个结点(bias unit)作为偏移值，其值为1。

5.hθ(x)为Logistic回归函数。

二.一些变量所代表的含义

为了方便描述神经网络，对一些变量进行描述（注意：此处的上标表示第几层，从1开始）：

x：最原始的输入

a：当前层的输出，其中a1(上标) = x

z：z = θx

有如下关系：

三.代价函数

1.代价函数：

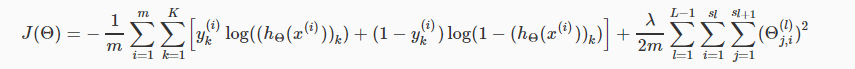
2.向量化后：

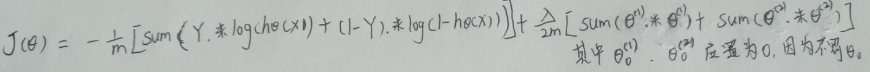
四.Forward Propagation

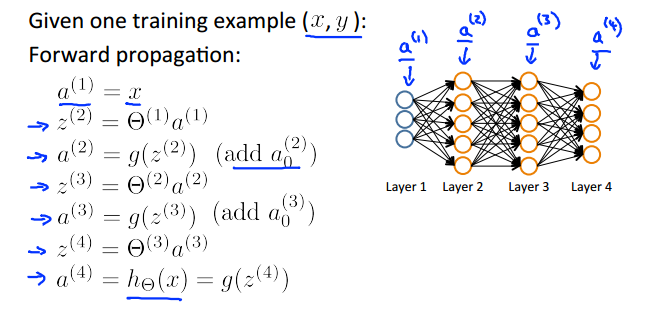
foward propagation就是将输入x，经过一层层的神经网络，最后到达输出层，并输出结果hθ(x)。

一张图可以很好地解释其过程：

五.Back Propagation（求梯度）

我们可以通过foward propagation求出输出结果hθ(x)，接下来就是要减少误差的而进行参数调整了，一贯的做法是梯度下降。

可知Logistic回归的梯度下降的表达式为：

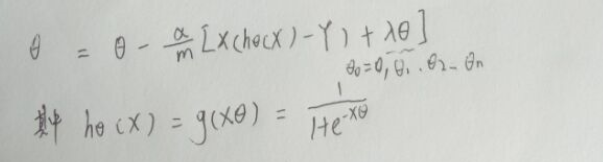
由于神经网络也是利用Logistic回归的sigmoid函数，那么其梯度下降的表达式也应该类似。

可知最后一层，也就是输出层的输出结果为hθ(x)，也就是预测值。那么误差就是hθ(x)-Y，对应了上式中的“(hθ(x)-Y)”，记δ=hθ(x)-Y。

但是，我们只知道最后一层的δ，即hθ(x)-Y，而隐藏层的δ却不能够直接看出来，那应该如何呢？

可知输出层的hθ(x)，是倒数第二层通过一定的规则计算出来的；反过来，倒数第二层计算所出现的误差，也可以通过输出层hθ(x)与真实值的误差反过来求。其中最重要的就是参数θ，因为它规定着输入(或输出)在当前结点所占的比例。

知道了Back Propagation的思想后，就需要着手具体如何求出δ了，其方法就是微积分中的“链式求导”。可知当前层的输出a(l)（可以看做一个变量），通过相关的映射（或者说函数）得出下一层的输出a(l+1)。此时把a(l+1) 看成y，a(l)看成x，而y = f(x)。我么已知y所造成的误差为δ，而y又是x的函数，所以x所造成的误差就等于：δ*f'(x)。与Logistic回归不同的是：神经网络在两层之间存在着n*m的全相连，每一条边都代表着a-->b的权重，即参数θ。在求误差δ的时候，应该乘上参数θ，如下：

因此，一直往前递推，就可以求出各层（输入层不需要求，因为总为0）的误差δ，即“(hθ(x)-Y)”。梯度就可以求出来了，之后就轮到梯度下降大显身手了。

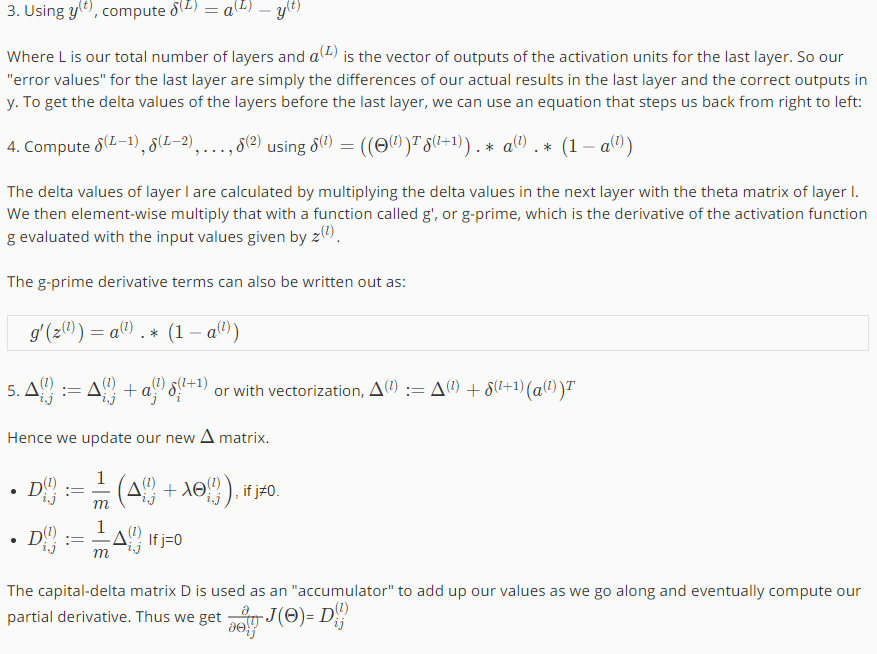
求梯度的过程总结：

六.算法流程：