hihocoder 1043 完全背包

#1043 : 完全背包

时间限制:20000ms

单点时限:1000ms

内存限制:256MB

描述

且说之前的故事里，小Hi和小Ho费劲心思终于拿到了茫茫多的奖券！而现在，终于到了小Ho领取奖励的时刻了！

等等，这段故事为何似曾相识？这就要从平行宇宙理论说起了………总而言之，在另一个宇宙中，小Ho面临的问题发生了细微的变化！

小Ho现在手上有M张奖券，而奖品区有N种奖品，分别标号为1到N，其中第i种奖品需要need(i)张奖券进行兑换，并且可以兑换无数次，为了使得辛苦得到的奖券不白白浪费，小Ho给每件奖品都评了分，其中第i件奖品的评分值为value(i),表示他对这件奖品的喜好值。现在他想知道，凭借他手上的这些奖券，可以换到哪些奖品，使得这些奖品的喜好值之和能够最大。

提示一： 切，不就是0~1变成了0~K么

提示二：强迫症患者总是会将状态转移方程优化一遍又一遍

提示三：同样不要忘了优化空间哦！

提示一： 切，不就是0~1变成了0~K么

令人欣慰的是，在这个平行世界里小Ho已经学习了一般的01背包问题，所以他并没有思考太久，便提出了自己的想法。

“我们的首要目标仍然是将问题抽象化！在我看来，这个问题其实和01背包问题很像，我们在解决01背包问题的时候是按照奖品的标号从1到N依次决定每件奖品是否选取，那么对于每种奖品有无数件的这个问题，我可以按照奖品的标号从1到N依次决定每种奖品选取的件数！”

小Hi点了点头表示赞同。

小Ho于是继续说道：“那么按照01背包的想法，我可以使用best(i, x)表示已经决定了前i件物品每件物品选择多少件，当前已经选取的物品的所需奖券数总和不超过x时，能够获取的最高的喜好值的和，那么最终的答案便是best(N, M)。”

小Hi道：”的确可以这样，那么你准备如何转移呢？”

小Ho道：“仍然是根据01背包的做法，对于一个问题best(i, x)，考虑最后一步——即第i件物品选择多少件，不妨就假设选择k件吧，那么k的取值范围肯定是在0~(x / need(i))这个范围内。这个时候我们可以知道best(i - 1, x - need(i) * k) + value(i) * k将会是一种可能的方案。”

小Hi挠了挠头，问道：”你所说的‘可能的方案’是什么意思？”

小Ho笑道：“就是说best(i, x)的求解满足这个公式~”

说罢，拿过纸笔，列出了一个式子。

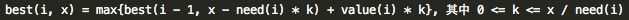
小Hi接过纸来，看完说道：“的确没错，总共就是这些可能~那你是否求解这个问题也是用与01背包类似的方法进行求解呢？”

“是的，我会使用这样的方法来做！”小Ho刷刷刷又在纸上写下来几行伪代码。

“应该没有问题，时间复杂度也很不错了~~但是我看着总有点难受！”小Hi点了点头又摇头。

“怎么说？”

      

提示二：强迫症患者总是会将状态转移方程优化一遍又一遍

小Hi嘻嘻笑了两声，说道：“我们不妨换一种问题定义的方式：用best(i, x)表示已经决定了前i件物品每件物品选择多少件，当前已经选取的物品的所需奖券数总和不超过x时，能够获取的最高的喜好值的和！”

小Ho仔仔细细回忆了下，确认小Hi所说和自己先前并无区别，怒道：“你这和我的定义方法有什么区别呀？”

小Hi道：“别急别急，这部分的确没有区别，有区别的在后头~”

小Ho撇了撇嘴：“那你就说呗~”

小Hi继续道：“我们还是考虑最后一步——要不要再选一件第i种奖品！”

小Ho有点不能理解，道：“什么叫再选一件？”

“你想想，在你的状态转移方程（即问题求解公式）中是否满足这样两个公式？”小Hi问道。

小Ho低头想了想，点了点头表示赞同。

小Hi于是继续问道：“那你有没有意识到这样一个等式？”

“似乎……是的！”小Ho惊道：“这么说，其实best(i, x)的大部分计算都在best(i, x - need(i))中已经计算过了！”

小Hi问出了最后一个问题：“所以你的公式是不是就可以变成这样子呢？”

“是的！所以……代码就可以这么写了~是么！”

“是的嗯~”

      

提示三：同样不要忘了优化空间哦！

详情请见hiho一下 第6周 01背包 提示二~

      

输入

每个测试点（输入文件）有且仅有一组测试数据。

每组测试数据的第一行为两个正整数N和M,表示奖品的种数，以及小Ho手中的奖券数。

接下来的n行描述每一行描述一种奖品，其中第i行为两个整数need(i)和value(i)，意义如前文所述。

测试数据保证

对于100%的数据，N的值不超过500，M的值不超过10^5

对于100%的数据，need(i)不超过2*10^5, value(i)不超过10^3

输出

对于每组测试数据，输出一个整数Ans，表示小Ho可以获得的总喜好值。

样例输入

5 1000
144 990
487 436
210 673
567 58
1056 897

样例输出

5940