【HDOJ】4373 Mysterious For

1. 题目描述
有两种不同类型的循环，并给出一个由1、2组成的序列，表示嵌套的循环类型。
问这样组着的循环一共需要多少次循环？并将结果模364875103。

2.基本思路
显然，每当遇到一个类型1的序列，即可以判定12...2的嵌套循环共多少次，而1类型的循环次数为常亮。
因此，将原序列从1分开，并将每个子序列的循环次数相乘即为总的循环次数。
1     共循环n次 = C[n][1]
12   共循环n*(n+1)/2次 = C[n+1][2]
122 共循环n*(n+1)*(n+2)/6次 = C[n+2][3]
12..2 |2|=m 共循环n*(n+1)*(n+2)/6次 = C[n+m-1][m]
由Lucas定理可知，假设p为素数，有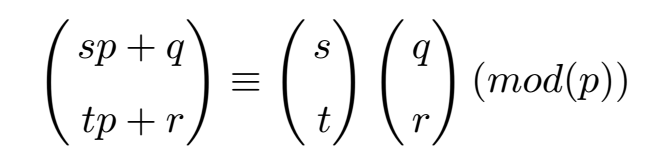

比较悲剧的是364875103是个合数，将它拆解为两个素数并使用LUCAS后，
我们可以知道ans=a1(mod p1), ans=a2(mod p2), 且p1, p2互素，求ans = ? (mod p1*p2)。
使用中国剩余定理。
使用欧拉定理求逆。

3. 代码

 /* 4373 */
 #include <iostream>
 #include <sstream>
 #include <string>
 #include <map>
 #include <queue>
 #include <set>
 #include <stack>
 #include <vector>
 #include <deque>
 #include <algorithm>
 #include <cstdio>
 #include <cmath>
 #include <ctime>
 #include <cstring>
 #include <climits>
 #include <cctype>
 #include <cassert>
 #include <functional>
 #include <iterator>
 #include <iomanip>
 using namespace std;
 //#pragma comment(linker,"/STACK:102400000,1024000")

 #define sti                set<int>
 #define stpii            set<pair<int, int> >
 #define mpii            map<int,int>
 #define vi                vector<int>
 #define pii                pair<int,int>
 #define vpii            vector<pair<int,int> >
 #define rep(i, a, n)     for (int i=a;i<n;++i)
 #define per(i, a, n)     for (int i=n-1;i>=a;--i)
 #define clr                clear
 #define pb                 push_back
 #define mp                 make_pair
 #define fir                first
 #define sec                second
 #define all(x)             (x).begin(),(x).end()
 #define SZ(x)             ((int)(x).size())
 #define lson            l, mid, rt<<1
 #define rson            mid+1, r, rt<<1|1
 #define LL                __int64

 const int maxn = ;
 const int mod1 = ;
 const int mod2 = ;
 const int mod = ;
 LL fact1[mod1+];
 LL fact2[mod2+];
 LL e1, e2;
 int pos[maxn];
 int n, m, k;

 LL Pow(LL base, LL n, LL mod) {
     LL ret = ;

     base %= mod;
     while (n) {
         if (n & )
             ret = ret * base % mod;
         base = base * base % mod;
         n >>= ;
     }

     return ret;
 }

 void init() {
     fact1[] = fact2[] = ;
     rep(i, , mod1)
         fact1[i] = fact1[i-] * i % mod1;
     rep(i, , mod2)
         fact2[i] = fact2[i-] * i % mod2;
     e1 = mod2 * Pow(mod2, mod1-, mod1);
     e2 = mod1 * Pow(mod1, mod2-, mod2);

     #ifndef ONLINE_JUDGE
         printf("e1 = %I64d, e2 = %I64d\n", e1, e2);
     #endif
 }

 LL C(LL n, LL m, LL mod, LL *fact) {
     if (n < m)    return ;
     return fact[n] * Pow(fact[m]*fact[n-m], mod-, mod) % mod;
 }

 LL Lucas(LL n, LL m, LL mod, LL *fact) {
     if (m == )    return ;
     return C(n%mod, m%mod, mod, fact) * Lucas(n/mod, m/mod, mod, fact);
 }

 void solve() {
     LL ans = , tmp;
     LL a1, a2;

     rep(i, , k) {
         m = pos[i+]-pos[i];
         a1 = Lucas(n+m-, m, mod1, fact1);
         a2 = Lucas(n+m-, m, mod2, fact2);
         tmp = (a1*e1 + a2*e2) % mod;
         #ifndef ONLINE_JUDGE
             printf("a1 = %I64d, a2=%I64d, tmp=%I64d\n", a1, a2, tmp);
         #endif
         ans = ans * tmp % mod;
     }

     printf("%I64d\n", ans);
 }

 int main() {
     ios::sync_with_stdio(false);
     #ifndef ONLINE_JUDGE
         freopen("data.in", "r", stdin);
         freopen("data.out", "w", stdout);
     #endif

     int t;

     init();
     scanf("%d", &t);
     rep(tt, , t+) {
         scanf("%d%d%d", &n, &m, &k);
         rep(i, , k)
             scanf("%d", &pos[i]);
         pos[k] = m;
         printf("Case #%d: ", tt);
         solve();
     }

     #ifndef ONLINE_JUDGE
         printf("time = %d.\n", (int)clock());
     #endif

     return ;
 }

4. 数据生成器

 from copy import deepcopy
 from random import randint, shuffle
 import shutil
 import string

 def GenDataIn():
     with open("data.in", "w") as fout:
         t = 20
         bound = 10**5
         fout.write("%d\n" % (t))
         for tt in xrange(t):
             n = randint(20, bound)
             m = randint(20, bound)
             k = randint(1, 15)
             fout.write("%d %d\n%d " % (n, m, k))
             L = [0]
             st = set()
             for i in xrange(1, k):
                 while True:
                     x = randint(1, m)
                     if x not in st:
                         break
                 L.append(x)
                 st.add(x)
             L = sorted(L)
             fout.write(" ".join(map(str, L)) + "\n")

 def MovDataIn():
     desFileName = "F:\eclipse_prj\workspace\hdoj\data.in"
     shutil.copyfile("data.in", desFileName)

 if __name__ == "__main__":
     GenDataIn()
     MovDataIn()