逻辑回归损失函数(cost function)

逻辑回归模型预估的是样本属于某个分类的概率，其损失函数(Cost Function)可以像线型回归那样，以均方差来表示；也可以用对数、概率等方法。损失函数本质上是衡量”模型预估值“到“实际值”的距离，选取好的“距离”单位，可以让模型更加准确。

1. 均方差距离

\[{J_{sqrt}}\left( w \right) = {\sum\limits_{i = 1}^m {{y_i}\left( {1 - p\left( {{x_i};w} \right)} \right)} ^2} + \left( {1 - {y_i}} \right){\left( {0 - p\left( {{x_i};w} \right)} \right)^2}{\rm{      (1)}}\]

用均方差作为损失函数，当模型完全预估错误时（y=1, p=0; 或y=0， p=1），损失是1。预估正确时，损失是0。错误值离正确值的“距离”相对较小，区分度不大。

另外，上面的损失函数相对\(\theta \)并非是凸函数，而是有很多极小值（local minimum）的函数。因此，很多凸优化的算法（如梯度下降）无法收敛到全局最优点。

2. log距离

均方差作为LR模型的距离衡量标准，最“预估错误”的惩罚太过柔和。因此，最后训练出来的模型会出现较多的“极端”预估错误情况。另外，均方差损失函数的非凸性也限制了其使用价值。

log距离作为损失函数的公式如下:

\[{J_{\log }}\left( w \right) = \sum\limits_{i = 1}^m { - {y_i}Log\left( {p\left( {{x_i};w} \right)} \right) - (1 - {y_i})Log\left( {1 - p\left( {{x_i};w} \right)} \right)} {\rm{        (2)}}\]

式（2）与式（1）的区别如下图所示：

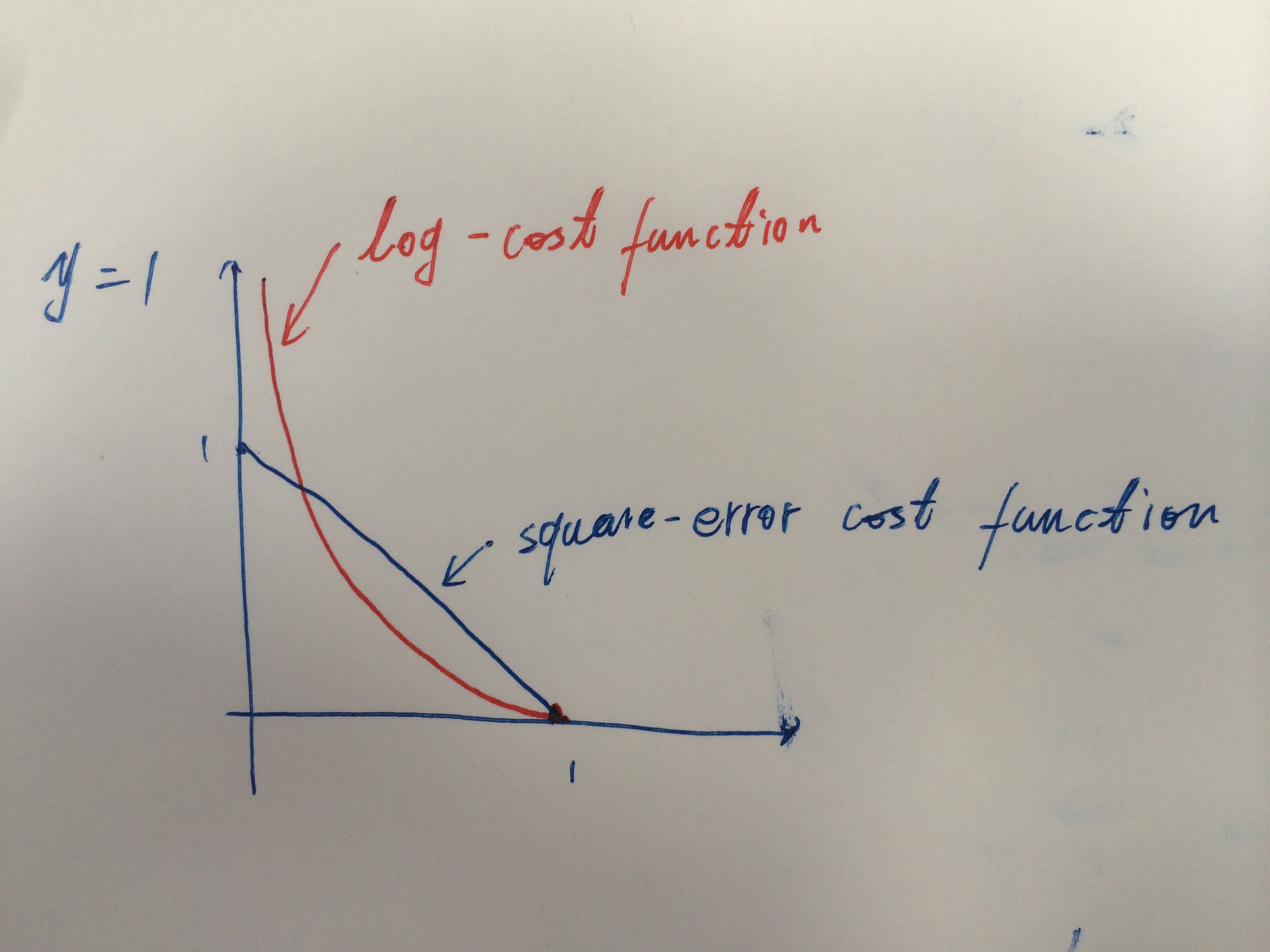
3. 概率距离

LR模型预估的是概率，自然的，损失函数可以用联合概率分布来衡量。

\[{J_{stat}}(w) =  - \prod\limits_{i = 1}^m {{{\left( {p({x_i};w)} \right)}^{{y_i}}}{{\left( {1 - p({x_i};w)} \right)}^{1 - {y_i}}}} {\rm{     (3)}}\]

比较式（2）和式（3）可知：

\[{J_{\log }}\left( w \right) = Log\left( {{J_{stat}}(w)} \right){\rm{     (4)}}\]

由于log函数为单调递增函数，log距离和概率距离本质上是一样的，训练得到的结果也应该一致。