Java实现最小费用最大流问题

1 问题描述

在最大流有多组解时，给每条边在附上一个单位费用的量，问在满足最大流时的最小费用是多少？

2 解决方案

下面代码所使用的测试数据如下图：

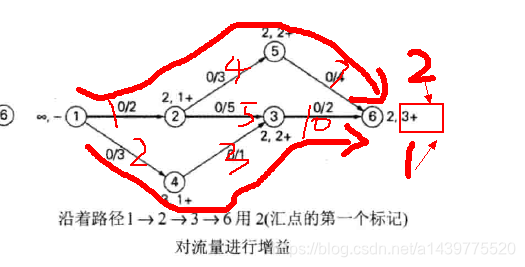
package com.liuzhen.practice;

import java.util.ArrayList;
import java.util.Scanner;

public class Main {
    public static int MAX = 1000;
    public static int n;   //图中顶点数目
    public static boolean[] used = new boolean[MAX];   //判断顶点是否在队列中
    public static int[] pre = new int[MAX];   //记录最短增广路径中相应节点的前节点
    public static int[] distance = new int[MAX];   //记录源点到图中其他所有顶点的最短距离
    public static int[] capacity = new int[MAX];  //用于记录遍历图每一次得到增广路径的流量
    public static ArrayList<edge>[] map;   //图的邻接表
    //表示图中边信息内部类
    static class edge {
        public int from;   //边的起点
        public int to;     //边的终点
        public int cap;    //边的容量
        public int cost;   //边的费用

        public edge(int from, int to, int cap, int cost) {
            this.from = from;
            this.to = to;
            this.cap = cap;
            this.cost = cost;
        }
    }
    //输入给定图数据
    @SuppressWarnings("unchecked")
    public void init() {
        Scanner in = new Scanner(System.in);
        n = in.nextInt();
        int k = in.nextInt();  //给定图的边数目
        map = new ArrayList[n];
        for(int i = 0;i < n;i++)
            map[i] = new ArrayList<edge>();
        for(int i = 0;i < k;i++) {
            int from = in.nextInt();
            int to = in.nextInt();
            int cap = in.nextInt();
            int cost = in.nextInt();
            map[from].add(new edge(from, to, cap, cost));  //正向边
            map[to].add(new edge(to, from, 0, -cost));     //反向边
        }
    }

    //寻找顶点start到顶点end的最短路径（PS：即费用最少的一条增广路径）
    public boolean spfa(int start, int end) {
        int[] count = new int[n];
        for(int i = 0;i < n;i++) {
            used[i] = false;
            pre[i] = -1;
            distance[i] = Integer.MAX_VALUE;
            capacity[i] = Integer.MAX_VALUE;
        }
        used[start] = true;
        pre[start] = start;
        distance[start] = 0;
        count[start]++;
        ArrayList<Integer> list = new ArrayList<Integer>();
        list.add(start);
        while(!list.isEmpty()) {
            int index = list.get(0);
            list.remove(0);
            used[index] = false;
            for(int i = 0;i < map[index].size();i++) {
                edge temp = map[index].get(i);
                if(temp.cap > 0 && distance[temp.to] > distance[index] + temp.cost) {
                    //记录顶点start到图中其它顶点之间的最短费用距离
                    distance[temp.to] = distance[index] + temp.cost;
                    pre[temp.to] = index;
                    //记录增广路径能够流通的最大流量
                    capacity[temp.to] = Math.min(capacity[index], temp.cap);
                    if(!used[temp.to]) {
                        used[temp.to] = true;
                        list.add(temp.to);
                        count[temp.to]++;
                        if(count[temp.to] > n)   //用于判断图中是否有负环
                            return false;
                    }
                }
            }
        }
        if(distance[end] != Integer.MAX_VALUE && pre[end] != -1)
            return true;
        return false;
    }

    public int getResult() {
        init();   //输入给定图数据
        int minCost = 0;
        int start = 0;   //把源点设置为顶点0
        int end = n - 1;  //把汇点设置为顶点n - 1
        while(true) {
            if(spfa(start, end) == false)
                break;
            System.out.println("增广路径增量："+capacity[end]+", 费用流："+distance[end]);
            minCost += distance[end] * capacity[end];
            int last = end;
            int begin = end;
            System.out.print("汇点出发");
            while(begin != start) {
                last = begin;
                begin = pre[last];
                int i = 0, j = 0;
                System.out.print("——>"+last);
                for(;i < map[begin].size();i++) {
                    if(map[begin].get(i).to == last)
                        break;
                }
                map[begin].get(i).cap -= capacity[end];  //正向边剩余流量减少
                for(;j < map[last].size();j++) {
                    if(map[last].get(j).to == begin)
                        break;
                }
                map[last].get(j).cap += capacity[end];  //反向边剩余流量增加
            }
            System.out.println("——>"+begin);
        }
        return minCost;
    }

    public static void main(String[] args) {
        Main test = new Main();
        int result = test.getResult();
        System.out.println(result);
    }
}

运行结果：

7
1 2 1
3 3 2
2 5 5
4 3 4
5 2 10
2 1 3
5 4 7
增广路径增量：2, 费用流：12
汇点出发——>5——>4——>1——>0
增广路径增量：1, 费用流：15
汇点出发——>5——>2——>3——>0