Java实现 LeetCode 391 完美矩形

391. 完美矩形

我们有 N 个与坐标轴对齐的矩形, 其中 N > 0, 判断它们是否能精确地覆盖一个矩形区域。

每个矩形用左下角的点和右上角的点的坐标来表示。例如， 一个单位正方形可以表示为 [1,1,2,2]。 ( 左下角的点的坐标为 (1, 1) 以及右上角的点的坐标为 (2, 2) )。

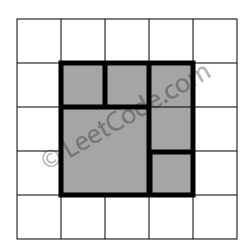
示例 1:

rectangles = [

[1,1,3,3],

[3,1,4,2],

[3,2,4,4],

[1,3,2,4],

[2,3,3,4]

]

返回 true。5个矩形一起可以精确地覆盖一个矩形区域。

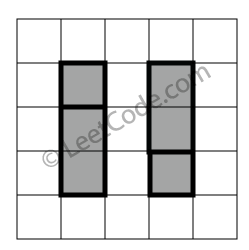
示例 2:

rectangles = [

[1,1,2,3],

[1,3,2,4],

[3,1,4,2],

[3,2,4,4]

]

返回 false。两个矩形之间有间隔，无法覆盖成一个矩形。

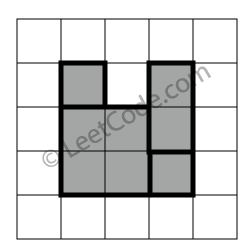
示例 3:

rectangles = [

[1,1,3,3],

[3,1,4,2],

[1,3,2,4],

[3,2,4,4]

]

返回 false。图形顶端留有间隔，无法覆盖成一个矩形。

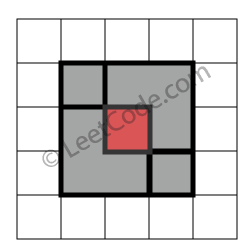
示例 4:

rectangles = [

[1,1,3,3],

[3,1,4,2],

[1,3,2,4],

[2,2,4,4]

]

返回 false。因为中间有相交区域，虽然形成了矩形，但不是精确覆盖。

PS：

如果是完美矩形 那么一定满足两点： （1）最左下 最左上 最右下 最右上 的四个点只出现一次 其他点成对出现 （2）四个点围城的矩形面积 = 小矩形的面积之和

class Solution {

    public boolean isRectangleCover(int[][] rectangles) {
        int left = Integer.MAX_VALUE;
        int right = Integer.MIN_VALUE;
        int top = Integer.MIN_VALUE;
        int bottom = Integer.MAX_VALUE;
        int n = rectangles.length;

        Set<String> set = new HashSet<>();
        int sumArea = 0;

        for (int i = 0; i < n; i++) {
            //获取四个点的坐标
            left = Math.min(left, rectangles[i][0]);
            bottom = Math.min(bottom, rectangles[i][1]);
            right = Math.max(right, rectangles[i][2]);
            top = Math.max(top, rectangles[i][3]);
            //计算总小矩形的面积
            sumArea += (rectangles[i][3] - rectangles[i][1]) * (rectangles[i][2] - rectangles[i][0]);
            //分别记录小矩形的坐标
            String lt = rectangles[i][0] + " " + rectangles[i][3];
            String lb = rectangles[i][0] + " " + rectangles[i][1];
            String rt = rectangles[i][2] + " " + rectangles[i][3];
            String rb = rectangles[i][2] + " " + rectangles[i][1];
            //如果有就移除 没有就加入
            if (!set.contains(lt)) set.add(lt);
            else set.remove(lt);
            if (!set.contains(lb)) set.add(lb);
            else set.remove(lb);
            if (!set.contains(rt)) set.add(rt);
            else set.remove(rt);
            if (!set.contains(rb)) set.add(rb);
            else set.remove(rb);
        }

        //最后只剩4个大矩形坐标且面积相等即为完美矩形
        if (set.size() == 4 && set.contains(left + " " + top) && set.contains(left + " " + bottom) && set.contains(right + " " + bottom) && set.contains(right + " " + top)) {
            return sumArea == (right - left) * (top - bottom);
        }
        return false;
    }
}