关于分频器的FPGA实现整理思路

分频器是用的最广的一种FPGA电路了，我最初使用的是crazybingo的一个任意分频器，可以实现高精度任意分频的一个通用模块，他的思想在于首先指定计数器的位宽比如32位，那么这个计数器的最大值就是2^32=4294967296，

假设系统时钟为50MHz，那么假如要想实现输出频率为fout，那么可以使用的频率控制字为：

K满足关系：

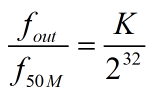，那么设计计数器在每个时钟上升沿累加的值为K，当计数值为2^31时，clkout=1;否则clkout=0.最终即可以实现任意频率的输出，精度的计算方法为当K=1时，可以得到clkout=0.0116415321826934814453125Hz，也即是说可以输出的最小频率为0.011Hz

此外我们最为常见的分频器分为以下4种分析：

1.偶数分频

最简单，要想得到分频系数为N的频率输出，设定一个计数器，这个计数器从零开始加1，当加到N/2-1时计数器清零，或者clkout翻转，以此循环，即可实现偶数倍分频。

2.奇数分频（分占空比不确定以及占空比50%）

方法一：分频系数为N，占总比不确定：以三（N）分频为例，上升沿触发计数，计数器计数到1（N-1）/2时输出时钟翻转，计数到2（N-1）时再次翻转.代码为产生1/11占空比为十一分频时钟：在计数值为9和10时均反转时钟，是产生抽样脉冲的有效方法：

always @(posedge clk or posedge rst) begin
              if(rst)begin   //复位
                     cnt<=;
                     clk_div11<=;
              end
              elseif(cnt==) begin
                     clk_div11<=~clk_div11;   //时钟翻转
                     cnt<=cnt+;    //继续计数
              end
              elseif(cnt==) begin
                     clk_div11<=~clk_div11;   //时钟翻转
                     cnt<=;    //计数清零
              end
              else
                     cnt<=cnt+;
       end

占空比50% ，则可以在上面的基础上，加上一个下降沿触发计数，然后将上升沿和下降沿产生的时钟进行相或运算，即可得到奇数分频输出。

reg clk1;
       reg[:]cnt1;
      always@(posedge clk or posedge rst) begin
              if(rst)begin   //复位
                     cnt1<=;
                     clk1<=;
              end
              elseif(cnt1==) begin
                     clk1<=~clk1;   //时钟翻转
                     cnt1<=cnt1+;    //继续计数
              end
              elseif(cnt1==) begin
                     clk1<=~clk1;   //时钟翻转
                     cnt1<=;    //计数清零
              end
              else
                     cnt1<=cnt1+;
       end

       reg clk2;
       reg[:]cnt2;
      always@(negedge clk or posedge rst) begin
              if(rst)begin   //复位
                     cnt2<=;
                     clk2<=;
              end
              elseif(cnt2==) begin
                     clk2<=~clk2;   //时钟翻转
                     cnt2<=cnt2+;    //继续计数
              end
              elseif(cnt2==) begin
                     clk2<=~clk2;   //时钟翻转
                     cnt2<=;    //计数清零
              end
              else
                    cnt2<=cnt2+;
       end

             assign clk_div3=clk1 | clk2;  //或运算

 
图1 50%占空比的三分频电路原理图

方法二：对进行奇数倍n分频时钟，先进行n/2分频，然后在二分频得到（这部分先讲半整数分频）

亲测有效代码：

module ModuloN_Cntr(input clk,rst,output clk_out);
reg [1:0]cnt1;
reg [1:0]cnt2;
reg temp1,temp2;
always@(posedge clk or negedge rst)
begin
    if(~rst)
    begin
        cnt1<=0;
        temp1<=0;
    end
    else
    begin
        if(cnt1==2)
        begin
            temp1<=1;
            cnt1<=0;
        end
        else
        begin
            cnt1<=cnt1+1;
            temp1<=0;
        end
    end
end
always@(negedge clk or negedge rst)
begin
    if(~rst)
    begin
        cnt2<=0;
        temp2<=0;
    end
    else
    begin
        if(cnt2==2)
        begin
            temp2<=1;
            cnt2<=0;
        end
        else
        begin
            cnt2<=cnt2+1;
            temp2<=0;
        end
    end
end
assign clk_out=temp1|temp2;
endmodule 

仿真波形：

3.半整数分频

半整数指的是N+0.5分频器设计：先进行模N+1计数，计数到N时输出时钟赋值为1，然后当计数到0时，输出时钟赋值为0，因此保持计数值为N的时间为半个时钟周期即为设计的关键，从中可以发现，计数器是在时钟的上升沿计数，那么我们可以让时钟在计数值为N时，将计数触发时钟翻转，时钟的下降沿变为上升沿，因此计数值为0，所以每产生一个N+0.5分频时钟周期，触发时钟都要翻转一次，以2.5分频为例程序如下：

 //异或运算

       assignclk_in=clk^clk_div2;

       //模3计数器

       reg clk_out;

       reg [1:0]cnt;

       always@(posedge clk_in or posedge rst) begin

              if(rst)begin   //复位

                     cnt<=0;

                     clk_out<=0;

              end

              elseif(cnt==1) begin

                     clk_out<=~clk_out;   //时钟翻转

                     cnt<=cnt+1;    //继续计数

              end

              elseif(cnt==2) begin

                     clk_out<=~clk_out;   //时钟翻转

                     cnt<=0;    //计数清零

              end

              else

                     cnt<=cnt+1;

       end

       //2分频

       reg clk_div2;

       always@(posedge clk_out or posedge rst) begin

              if(rst)  clk_div2<=0;  //复位

              else  clk_div2=~clk_div2;

       end

 
图3 通用半整数分频器的电路原理图

 
图4  2.5倍分频器时序仿真图

那么5.5分频呢：

代码：通用的这里N=5；

module ModuloN_Cntr(clk,clk_div,temp1,temp2);//N+0.5
input clk;
output clk_div;
reg[:]cnt1=;
reg[:]cnt2=;
output reg temp1,temp2;
initial begin temp1=;temp2=;end   //首先进行初始化，temp1=0;temp2=1
parameter N=;  //设定分频系数为N+0.5
always @(posedge clk)  //temp1上升沿跳变
begin
if(cnt1==*N)  //2*N
begin cnt1[:]<='d0;end
else begin cnt1[:]<=cnt1[:]+'d1;end
if(cnt1=='d0) begin temp1<=1;end   //高电平时间为N+1;
if(cnt1==N+) begin temp1<=;end   //低电平时间为N;
end
always@(negedge clk)  //temp2下降沿跳变
begin
if(cnt2==*N)  //2*N
begin cnt2[:]<='d0;end
else begin cnt2[:]<=cnt2[:]+'d1;end
if(cnt2=='d0) begin temp2<=0;end     //低电平时间为N;
if(cnt2==N) begin temp2<=;end    //高电平时间为N+1;
end
assign clk_div=temp1&&temp2;  //逻辑与
endmodule
//如果要进行N+0.5分频
//思路：总的来说要进行N+1+N=2N+1次分频
//在时钟的上升沿和下降沿都进行跳变
//上升沿进行占空比为N+1比N的时钟temp1;
//下降沿进行占空比为N比N+1的时钟temp2;
//最后div=temp1&&temp2 即可得到所需要的半整数分频

仿真波形：

4.任意小数分频

小数分频器的实现方法有很多中，但其基本原理都一样的，即在若干个分频周期中采取某种方法使某几个周期多计或少计一个数，从而在整个计数周期的总体平均意义上获得一个小数分频比。一般而言，这种分频由于分频输出的时钟脉冲抖动很大，故在设计中的使用已经非常少。但是，这也是可以实现的。以8.7倍分频为例，本文仅仅给出双模前置小数分频原理的verilog代码及其仿真图（如图6），具体原理可以参考刘亚海的《基于FPGA的小数分频器的实现》以及毛为勇的《基于FPGA的任意小数分频器的设计》。

还是放下代码吧：

//8分频
       reg clk_div8;
       reg[:]cnt_div8;
       always@(posedge clk or posedge rst) begin
              if(rst)begin  //复位
                     clk_div8<=;
                     cnt_div8<=;
              end
              elseif(cnt_div8=='d7) begin
                     clk_div8<=;   //置1
                     cnt_div8<=;
                 end
              elseif(cnt_div8=='d0) begin
                     clk_div8<=;  //置0
                     cnt_div8<=cnt_div8+;
              end
              else
                     cnt_div8<=cnt_div8+;
         end

         //9分频
       reg clk_div9;
       reg[:]cnt_div9;
       always@(posedge clk or posedge rst) begin
              if(rst)begin  //复位
                     clk_div9<=;
                     cnt_div9<=;
              end
              elseif(cnt_div9=='d8) begin
                     clk_div9<=;   //置1
                     cnt_div9<=;
                 end
              elseif(cnt_div9=='d0) begin
                     clk_div9<=;  //置0
                     cnt_div9<=cnt_div9+;
             end
              else
                     cnt_div9<=cnt_div9+;
         end
              //控制信号
       parameterDiv8Num=;
       reg ctrl;
       reg[:]AddValue;
       always@(posedge clk or posedge rst) begin
              if(rst)begin  //复位
                     ctrl<=;
                     AddValue<=-;
                  end
              elseif(AddValue<) begin
                     ctrl<=;
                     AddValue<=AddValue+Div8Num;
              end
             else begin
                     ctrl<=;
                     AddValue<=AddValue-;
              end
       end

       //选择输出
       reg clk_out;
       always @(ctrlor posedge clk or posedge rst) begin
              if(rst)  clk_out<=;  //复位
              elseif(ctrl)  clk_out<=clk_div8;
              elseclk_out<=clk_div9;
       end

 
图6  8.7分频器的时序仿真图

 

4、总结分频器是FPGA的基础，而且在FPGA逻辑电路设计的时候是经常使用的，希望大家对以上的整数倍分频和半整数倍分频能熟练掌握