hdoj 1874 dijkstra

在做PAT的甲1003，思考DFS和图什么的，时间紧张直接去看柳神（日后上传柳神的C++版本）的订阅，得知是dijkstra，转去用hdoj 1874练手，写了两天，终于调出来了

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=1874

题目大意：给你点 和 边的数目，接下来输出边的信息（a, b, c表示a和b之间距离为c），最后给你两个数字，表示两点的点信息。让你输出最短路径，没有就-1.

解题思路：dijkstra的思想是贪心，越想越经典。

起始动作就是从出发点开始，把其余所有点到出发点的最近距离存储下，

接下来的动作就是逐渐辐射，

方法是：存储：找到距离出发点最近的点记录下来（从存储的所有点中遍历），这个点就是出发点到这个点的最近距离，

　　批量处理：下一次把这个点作为过渡，如果 起点到这个点+这个点到其他某点的距离 < 起点直接到其他某点的距离，就把 起点直接到某点的距离更新为通过过度得到的距离，相当于把所有的更新存储的一下。

再接着执行，直到没有新的点可以加入作为过度为止（注意：每次得出的过度点是上一次得到的，然后上一次得到过度点就是起始点到过度点的最近距离）->（这段话我是脑子里有个这幅图B站女老师（主要学习思路））

上段思路我是理解了，可以写出，可以看懂

那么接下来说一下原理，和怎么想到的

上图：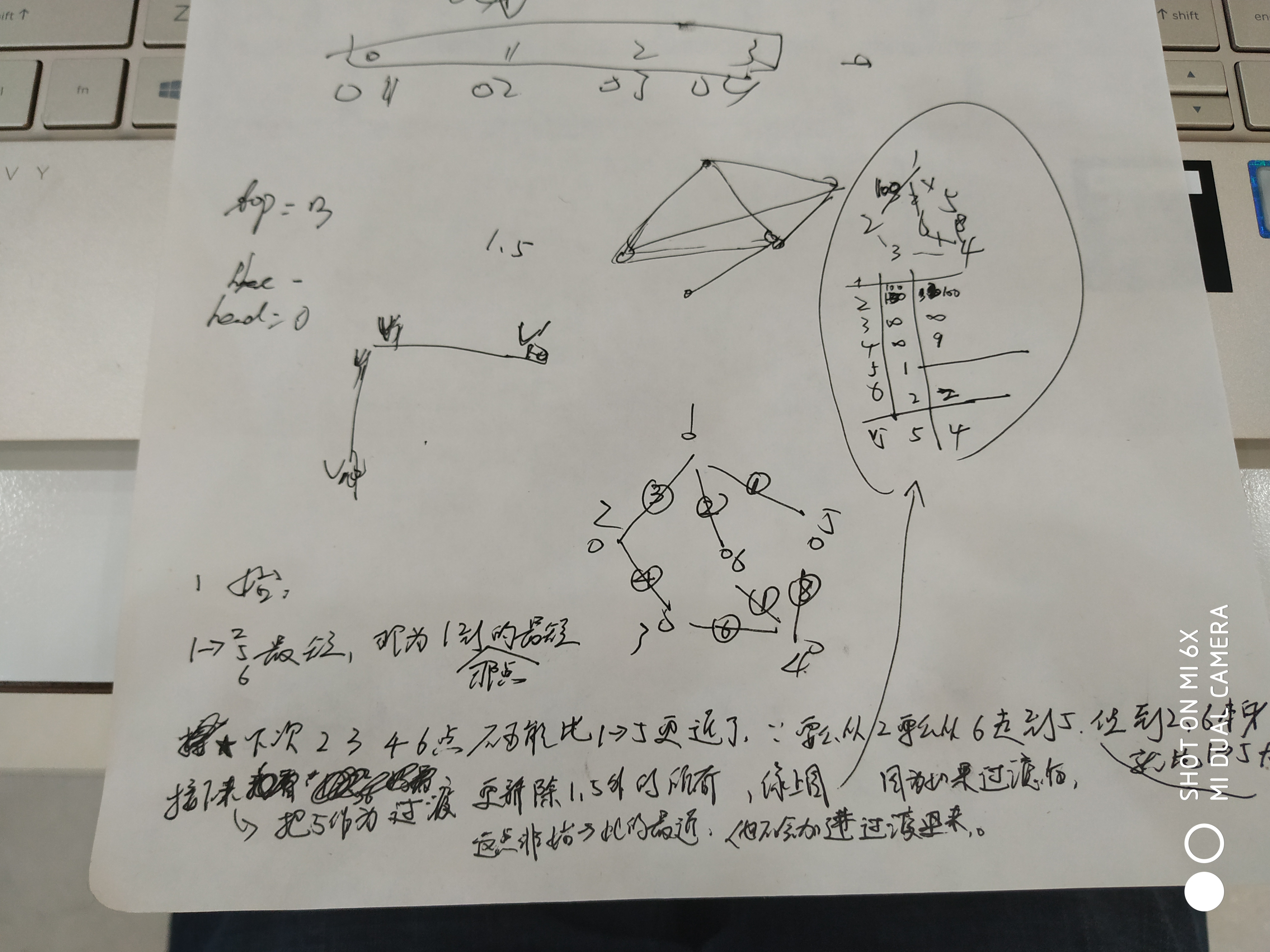

用到的资料：直接看柳神题解得知是dijkstra，用到的学习资料，B站女老师（主要学习思路），CSDN（主要看看代码思路）

看着不错的界面但是没去看的资料：博客园，CSDN1，CSDN2，CSDN3

dijkstra基础题陈列：https://www.cnblogs.com/ACMan/archive/2012/07/23/2605673.html

动态演示：我反应慢，思维也慢，没跟上https://www.cnblogs.com/ly199553/p/5547808.html

卿学姐代码风格：https://www.bilibili.com/video/av4224493/?spm_id_from=333.788.videocard.3

容易WA的地方：

1.重边的处理
2.起点与终点相同的情况

参考：http://acm.hdu.edu.cn/discuss/problem/post/reply.php?postid=36571&messageid=1&deep=0

代码：

 /***************************************
 * About:    hdoj 1874(Dijkstra)
 * Author:   GerJCS
 * B log:
 From: 19/2/27
 ***************************************/

 /*

 思路
 */

 //#include<bits/stdc++.h>
 #include<cstdio>
 #include<cstring>
 using namespace std;
 #define INF 999999
 int e[][];
 int visit[];
 int dis[];
 int m, n;
 int a, b, c;
 int start, end;
 void init1()
 {
     for(int i = ; i < m; i ++)
         for(int j = ; j < m; j ++){
             if(i == j)
                 e[i][j] = ;
             else{
                 e[i][j] = INF;
                 e[j][i] = INF;
             }
         }
 }
 void init2()
 {
     for(int i = ; i < m; i ++)
         visit[i] = ;
     visit[start] = ;
     for(int i = ; i < m; i ++)
         dis[i] = e[start][i];
 }
 //int dijkstra()
 void dijkstra()
 {
     int u = -;
     int min;
     for(int i = ; i < m - ; i ++)
     {
         min = INF;
         for(int j = ; j < m; j ++)
         {
             if(!visit[j] && min > dis[j])
             {
                 min = dis[j];
                 u = j;
             }
         }
 //        if(u == -1)
 //            return -1;
 //        if(u == end)
 //            return dis[u];
         visit[u] = ;
         for(int k = ; k < m; k ++)
             if(!visit[k] && dis[k] > dis[u] + e[u][k])
                 dis[k] = dis[u] + e[u][k];
     }
 //    return -1;
 }
 int main()
 {
 //    freopen("C:/Users/GerJCS岛/Desktop/ddd.txt","r",stdin);
 //    freopen("C:/Users/GerJCS岛/Desktop/out2.txt","w",stdout);
     while(scanf("%d%d", &m, &n) != EOF)
     {
         memset(e, , sizeof(e));
         memset(visit, , sizeof(visit));
         memset(dis, , sizeof(dis));
         init1();
         for(int i = ; i < n; i ++)
         {
             scanf("%d%d%d", &a, &b, &c);
 //            e[a][b] = c;
 //            e[b][a] = c;
             if(c < e[a][b]){
                 e[a][b] = c;
                 e[b][a] = c;
             }
         }

         scanf("%d%d", &start, &end);
         init2();
         dijkstra();
 //        printf("%d\n", dijkstra());
         if(dis[end] == INF)
             printf("-1\n");
         else
             printf("%d\n", dis[end]);
     }
 }

 //3 4
 //0 1 1
 //0 2 1
 //1 2 1
 //0 2 9
 //0 2

------------------------------------------------------------------------------待更新！-----------------------------------------------------------------------------

工具：http://tool.chinaz.com/Tools/textencrypt.aspx

密码：139*****136

加密后文字：

U2FsdGVkX19wgyNcTGQ7XiAr3GegDzjioUFtqCDiTpEjH3U8PCn0MGej0sbXbpmJ
/ek4/l8Di9oGOAFRHkQNZM4aRC474gAVDVi2L4FYs4rLjuxbYGh4ZydVxcVBXQPc
muey88tUTJJ0JpIUI7BR3teM9rtWec4JEWB/1H2khm6j+T+mm2qv+DpUcjZCWpoG
tRgFhQEnHfORwj95LI98+zPWjTC4ggmDYr21JleIbFaZ6CmbsiX/XtxkOAUZrz6q
8xwj+BRUyCxwjl0aR+98SgtY/HRw1B1hFMYk/Lm5Q41Fk+EXSsFvHI9UI3l4HNZe
g/LcjheiRBV3N5o4AH9qnLJIFhO0zFzzk9x0bM5/svtUEJVXpRqNjimx+vtuBSCi
d6oJbvI3dqVx7b7ukUOe0X6r0cAa5OFbbtR9+qNSBMiT6GKDb0riT8YP9c2PcOv4
phEJ83vWJtfTAf+g+upsGZtM3dT/yTRMdYwyVxkWvtoRl53PYm6/xOvgAuUOKWAF
thfH+nE3SHskAC/hOIVFue7R8bmFI8Ld/vG04bTTwmgM1rh+BwDEpCDuaExlUFI/
oanl8bCb66gMP/20XhHUzUZv6JsF6HmQPBfIw4ikcYboCk4lTLlu3oQYi7qy1hSs
km9uuBYFBc3ygaxjW//zTWYW5HOKPCp05p/q+/wYvEYC1OyChrocHpqhD7dB4FSR
oPWUvTvNS5ym4QsXnzzXLZ9CoYAic8iWWKMM/CPC5BOaolwdvlGM9zLDdoTqxqJ5
JiYndAf47DMXOxVUle9VvKv1MvL7Xk5qajPHVn9p5mHkdQicb0W64JLGA3DeZIQ/
f8i/KiKFwJxIs2qxjfj9DuF/P8kSbIJmE+ayJ5Yiml38bY6d+KDsQf0wNsc527Fr
vKouoogXgmINlHuly5Zy+iob6y8DbFzOgP2u9kow87zCEgSntpr9BGhP6wNyp5xp
LVkkfz5rXKrAJMIFCmJhMht8E//LYQmdJkTUsUqbF3MZc40HfQPE4LUfdRUBNTkj
O8hE6hLDNXQgXgO26Mf441T2FRKQYPH/3DYYlnRgly57kwBOu2wjpKC6WsE4JJWJ
683mzF/dTZxaNE+c6uAdbNvKUiETr4dlWXktIUWZO+Zo2SHVGvd9/lR0x354Wf/B
/YxZwv8mJxAI4qCSQVHwZEQlSRAHTpuqPxqZPd2dpB9YiB5+uEw6li4MEgESYsVk
YQJvbEDHBTH6R9RitJ79GBWOpPDs5HbBK5B1BWSgbLdRxvnWeV/DV9dnnA6smEDw
qBP2tmfTg/qTvaHYKj3xQkqGV3xFteiET1NRGlt+zhxc0axf3lMfdxecLlAy6zEU
Nv4MKTufILpY0dp1iy/uQLTkRLj8uCoEbK1e+CDNSNPS39rZwhfJjTol5CracvHs
RMDONEfHbEyxyoBmDgJUXjnUALTncc+4trIigiWOX0F/bz5lFU7Y/MCftzo+xpvV
9ChBNReSnry9/+m0UXEh124X362L+dqCb5iK+Nx1LE2iIKFs7GmT2m9u3pLFu1YR
On9UFXZiN15zsCgzU4+X2dLvc1CSlrOZAt2AUpgjdZ/4iDJqom3CDoBQNr0/I9Vt
7fUqnlXliPbe51uyJqX8fsbd27ty5vnG8mrdz+m6/mc=

人权！资本！圈子！平台！