09_EM算法

　　今天是2020年3月5日星期四。预计开学时间不会早于四月初，真是好消息，可以有大把的时间整理知识点（实际上发文章的时间都6月6号了，希望9月份能开学啊，不耽误找工作~）。每次导师找，整个人会变的特别烦躁，烦躁加不安，其它事情一点都做不下去，焦虑。改小论文这几天耽误了一些时间，查了些EM算法的例子，怎样理解这个算法呢？通过这周的学习，觉得数学公式有点唬人，但却是理解该算法最好的形式。

　　刚开始对这个算法一无所知，通过知乎、CSDN看资料，看白板视频，看讲解例子。越看例子越觉得负担重，因为要先把例子理解了，再去理解这个知识点。例子不能彻底理解，知识点也走不下去，倒不如一遍一遍的看数学公式。看完了公式，再去看例子，朦朦胧胧的就懂了。之后再去看白板视频，绝对是不一样的体验。

　　先看别人的视频，然后自己去推导公式，你会觉得困难摸不到头脑；先自己去推导公式，再去看别人视频，你会觉得心旷神怡一目了然。第一种做法，往往看视频的时候就是懵懵哒，抓不住别人讲述的重点；第二种做法，类似于先学会了九阳神功，再去和别人切磋武艺。初心是将《统计学习方法》这本书做详细的心得笔记，现在有点松动，希望能坚持下去。

---

GitHub：https://github.com/wangzycloud/statistical-learning-method

---

EM算法

引入

　　EM算法应该作为一种通用的求解方法，用于含有隐变量的概率模型参数的极大似然估计。拆开来看，这句话是应用在概率模型上的；用来估计概率模型的参数；类似于极大似然估计；求解的是含有隐变量的概率模型。那么问题来了，什么是该有隐变量的概率模型？概率模型是什么样子？极大似然估计？该方法是怎么进行计算的呢？

　　通常来讲，EM算法是一种迭代算法，每次迭代由两步组成：E步，求期望；M步：求极大，所以该算法被称为期望极大算法。说该算法可以作为一种通用的求解方法，原因在于：该算法不是NBM、LR、SVM这类解决相应场景的模型，而是可以用于求解含有隐变量概率模型的参数估计。

　　提到模型，脑子里第一印象有判别模型、生成模型。这里的概率模型自然和判别模型、生成模型不在同一个层次。在我的理解里，概率模型是类似于朴素贝叶斯算法这种，用概率来表示最后的分类标准；而不是感知机、SVM这种利用确信度来表达分类结果的模型。再考虑一下朴素贝叶斯算法，特征向量里的随机变量X，以及表示类别的随机变量Y，都是可以被观测到变量。在所有随机变量都可以观测到的情况下，我们可以利用极大似然估计来求解模型的参数。对于含有隐变量的概率模型，要如何求解呢？含有隐变量意味着不能观测到数据的全部状况，也就没有办法直接利用极大似然估计来求解。

　　现在看到的EM算法，就是一种求解含有隐变量的概率模型参数的极大似然估计方法。

EM算法

　　书本上三硬币模型，挺好的~代码已整理到github中，实际上就是把书本公式用代码实现出来...难度不大。

　　文中提到，该问题没有解析解，只有通过迭代的方法进行求解。仔细观察一下公式(9.4)，log(x)作用在公式(9.3)上，很明显log连乘可以变成连加，但连加式子中的每个项仍然是连加式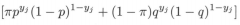。好像是因为这个原因，就无法得到解析解了。个人对数学不感冒，只能硬性的记住“不容易求解析解”这点，至于原因，实在是搞不懂啊。虽然无法得到解析解，但我们可以通过EM算法求解，大致步骤如下：

　　一般的，用Y表示观测随机变量的数据，Z表示隐随机变量的数据，Y和Z连在一起称为完全数据，观测数据Y又称为不完全数据。假设给定观测数据Y，其概率分布是P(Y|θ)，其中θ是需要估计的模型参数，那么不完全数据Y的似然函数是P(Y|θ)，对数似然函数L(θ)=logP(Y|θ)，假设Y和Z的联合概率分布是P(Y,Z|θ)，那么完全数据的对数似然函数是logP(Y,Z|θ)。

　　EM算法通过迭代求解L(θ)=logP(Y|θ)的极大似然估计，每次迭代由两个步骤：E步，M步组成。

　　文中对Q函数做了具体解释：

　　关于EM算法的几点说明，应该挺好理解的吧。步骤(1)，迭代求解的方式需要一步步接近极值，是在某个解的基础上，进一步求解。在最开始的时候，初值是任意选择的，并且正是因为初值任意选择，容易陷入局部极值，也就是对初值的选择非常敏感（对比一下梯度下降的过程）。步骤(2)，我们要清楚，求解的对象是变元参数θ。步骤(3)，极大化的过程，详见下图~（θ,L(θ))图像。步骤(4)，迭代停止条件。

　　EM算法的导出、收敛性，以及推广详见下图吧~搞了四五天，弄了个流程...

GMM高斯混合模型

　　书中公式一大堆，不太友好，手写代码的过程，就是把书本公式复现了一遍。难度不大，我认为需要先了解GMM模型是啥，再通过例子，熟悉一下计算过程，就可以掌握了。

　　还是从生成数据的角度看，由GMM模型生成一个数据，是要根据一个普通的多项式分布αk，来选择第k个高斯分布，分两步生成数据。但是，这里获得的数据，并不知道来自第几个αk，这就是隐变量了。

　　对于高斯混合模型的参数估计，可以通过EM算法求解。

　　1.明确隐变量，写出完全数据的对数似然函数。

　　2.EM算法的E步：确定Q函数。

　　3.确定EM算法的M步。

　　具体公式(9.26)-公式(9.32)就不一一摘录了，github已复现。算法描述如下：

　　本节整理的内容有些水...