机器学习3- 一元线性回归+Python实现

目录

• 1. 线性模型
• 2. 线性回归
  • 2.1 一元线性回归
• 3. 一元线性回归的Python实现
  • 3.1 使用 stikit-learn
    • 3.1.1 导入必要模块
    • 3.1.2 使用 Pandas 加载数据
    • 3.1.3 快速查看数据
    • 3.1.4 使用 stlearn 创建模型
    • 3.1.5 模型评估
  • 3.2 手动实现
    • 3.2.1 计算 w 和 b
    • 3.2.2 功能封装

1. 线性模型

给定 \(d\) 个属性描述的示例 \(\boldsymbol{x} = (x_1; x_2; ...; x_d)\)，其中 \(x_i\) 为 \(\boldsymbol{x}\) 在第 \(i\) 个属性上的取值，线性模型（linear model）试图学得一个通过属性的线性组合来进行预测的函数，即：

\[f(\boldsymbol{x}) = w_1x_1 + w_2x_2 + ... + w_dx_d +b \tag{1.1}
\]

使用向量形式为：

\[f(\boldsymbol{x}) = \boldsymbol{w}^T\boldsymbol{x}+b \tag{1.2}
\]

其中 \(\boldsymbol{w} = (w_1;w_2;...;w_d)\)，表达了各属性在预测中的重要性。

2. 线性回归

给定数据集 \(D = \lbrace(\boldsymbol{x}_1,{y}_1), (\boldsymbol{x}_2,{y}_2), ..., (\boldsymbol{x}_m,{y}_m)\rbrace\)，其中 \(\boldsymbol{x}_i = (x_{i1}; x_{i2}; ...; x_{id})\)，\(y_i \in \mathbb{R}\)。线性回归（linear regression）试图学得一个能尽可能准确地预测真实输出标记的线性模型，即：

\[f(\boldsymbol{x}_i) = \boldsymbol{w}^T\boldsymbol{x}_i+b \text{，使得} f(\boldsymbol{x}_i) \simeq y_i\tag{2.1}
\]

2.1 一元线性回归

先只考虑输入属性只有一个的情况，\(D = \lbrace({x}_1,{y}_1), ({x}_2,{y}_2), ..., ({x}_m,{y}_m)\rbrace\)，\(x_i \in \mathbb{R}\)。对离散属性，若属性值存在序（order）关系，可通过连续化将其转化为连续值。

如”高度“属性的取值“高”、“中”、“低”，可转化为\(\{1.0, 0.5, 0.0\}\)。

若不存在序关系，则假定有 \(k\) 种可能的属性值，将其转化为 \(k\) 维向量。

如“瓜类”属性的取值有“冬瓜”、“西瓜”、“南瓜”，可转化为 \((0,0,1),(0,1,0),(1,0,0)\)。

线性回归试图学得：

\[f(x_i) = wx_i+b\text{，使得}f(x_i)\simeq y_i \tag{2.2}
\]

为使 \(f(x_i)\simeq y_i\)，即：使 \(f(x)\) 与 \(y\) 之间的差别最小化。

考虑回归问题的常用性能度量——均方误差（亦称平方损失（square loss）），即让均方误差最小化：

\[\begin{aligned}
(w^*,b^*) = \underset{(w,b)}{arg\ min}\sum_{i=1}^m(f(x_i)-y_i)^2 \\
= \underset{(w,b)}{arg\ min}\sum_{i=1}^m(y_i-wx_i-b)^2
\end{aligned}
\tag{2.3}
\]

\(w^*,b^*\) 表示 \(w\) 和 \(b\) 的解。

均方误差对应了欧几里得距离，简称欧氏距离（Euclidean distance）。

基于均方误差最小化来进行模型求解的方法称为最小二乘法（least square method）。在线性回归中，就是试图找到一条直线，使得所有样本到直线上的欧氏距离之和最小。

下面需要求解 \(w\) 和 \(b\) 使得 \(E_{(w,b)} = \sum\limits_{i=1}^m(y_i-wx_i-b)^2\) 最小化，该求解过程称为线性回归模型的最小二乘参数估计（parameter estimation）。

\(E_{(w,b)}\) 为关于 \(w\) 和 \(b\) 的凸函数，当它关于 \(w\) 和 \(b\) 的导数均为 \(0\) 时，得到 \(w\) 和 \(b\) 的最优解。将 \(E_{(w,b)}\) 分别对 \(w\) 和 \(b\) 求导数得：

\[\frac{\partial{E_{(w,b)}}}{\partial(w)} = 2\Big(w\sum_{i=1}^m x_i^2 - \sum_{i=1}^m (y_i-b)x_i\Big) \tag{2.4}
\]

\[\frac{\partial{E_{(w,b)}}}{\partial(b)} = 2\Big(mb - \sum_{i=1}^m (y_i-wx_i)\Big) \tag{2.5}
\]

令式子 (2.4) 和 (2.5) 为 \(0\) 得到 \(w\) 和 \(b\) 的最优解的闭式（closed-form）解：

\[w = \frac{\sum_\limits{i=1}^m y_i(x_i-\overline{x})}{\sum\limits_{i=1}^m x_i^2 - \frac{1}{m}\Big(\sum\limits_{i=1}^m x_i\Big)^2} \tag{2.6}
\]

\[b = \frac{1}{m}\sum_{i=1}^m (y_i-wx_i) \tag{2.7}
\]

其中 \(\overline{x} = \frac{1}{m}\sum\limits_{i=1}^m x_i\) 为 \(x\) 的均值。

其他解法：

\[方差\ var(x) = \frac{\sum\limits_{i=1}^m(x_i-\bar{x})^2}{m-1}
\]

\[协方差\ cov(x,y) = \frac{\sum_\limits{i=1}^m (x_i-\overline{x})(y_i-\overline{y})}{n-1}
\]

\[w = \frac{cov(x,y)}{var(x)} = \frac{\sum_\limits{i=1}^m (x_i-\overline{x})(y_i-\overline{y})}{\sum\limits_{i=1}^m (x_i-\overline{x})^2}
\]

\[b = \bar{y} - w\bar{x}
\]

3. 一元线性回归的Python实现

现有如下训练数据，我们希望通过分析披萨的直径与价格的线性关系，来预测任一直径的披萨的价格。

其中 Diameter 为披萨直径，单位为“英寸”；Price 为披萨价格，单位为“美元”。

3.1 使用 stikit-learn

3.1.1 导入必要模块

import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from sklearn.linear_model import LinearRegression

3.1.2 使用 Pandas 加载数据

pizza = pd.read_csv("pizza.csv", index_col='Id')
pizza.head()  # 查看数据集的前5行

3.1.3 快速查看数据

我们可以使用 matplotlib 画出数据的散点图，x 轴表示披萨直径，y 轴表示披萨价格。

def runplt():
    plt.figure()
    plt.title("Pizza price plotted against diameter")
    plt.xlabel('Diameter')
    plt.ylabel('Price')
    plt.grid(True)
    plt.xlim(0, 25)
    plt.ylim(0, 25)
    return plt

dia = pizza.loc[:,'Diameter'].values
price = pizza.loc[:,'Price'].values
print(dia)
print(price)
plt = runplt()
plt.plot(dia, price, 'k.')
plt.show()

[ 6  8 10 14 18]
[ 7.   9.  13.  17.5 18. ]

3.1.4 使用 stlearn 创建模型

model = LinearRegression()  # 创建模型
X = dia.reshape((-1,1))
y = price
model.fit(X, y)  # 拟合

X2 = [[0], [25]] # 取两个预测值
y2 = model.predict(X2)  # 进行预测
print(y2)  # 查看预测值

plt = runplt()
plt.plot(dia, price, 'k.')
plt.plot(X2, y2, 'g-')  # 画出拟合曲线
plt.show()

[ 1.96551724 26.37284483]

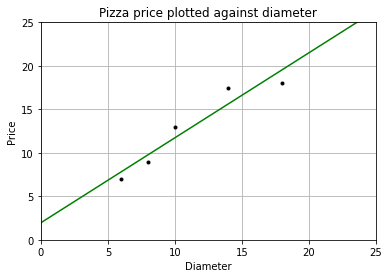
这里 fit()方法学得了一元线性回归模型 \(f(x) = wx+b\)，这里 \(x\) 指披萨的直径，\(f(x)\) 为预测的披萨的价格。

fit() 的第一个参数 X 为 shape(样本个数，属性个数) 的数组或矩阵类型的参数，代表输入空间；

第二个参数 y 为 shape(样本个数,) 的数组类型的参数，代表输出空间。

3.1.5 模型评估

成本函数（cost function）也叫损失函数（lost function），用来定义模型与观测值的误差。

模型预测的价格和训练集数据的差异称为训练误差（training error）也称残差（residuals）。

plt = runplt()
plt.plot(dia, price, 'k.')
plt.plot(X2, y2, 'g-')

# 画出残差
yr = model.predict(X)
for index, x in enumerate(X):
    plt.plot([x, x], [y[index], yr[index]], 'r-')

plt.show()

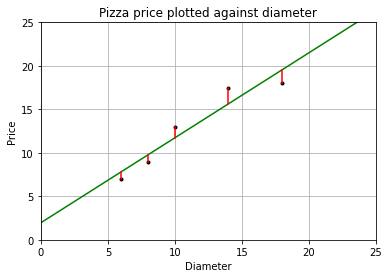
根据最小二乘法，要得到更高的性能，就是让均方误差最小化，而均方误差就是残差平方和的平均值。

print("均方误差为: %.2f" % np.mean((model.predict(X)-y) ** 2))

均方误差为: 1.75

3.2 手动实现

3.2.1 计算 w 和 b

\(w\) 和 \(b\) 的最优解的闭式（closed-form）解为：

\[w = \frac{\sum_\limits{i=1}^m y_i(x_i-\overline{x})}{\sum\limits_{i=1}^m x_i^2 - \frac{1}{m}\Big(\sum\limits_{i=1}^m x_i\Big)^2} \tag{2.6}
\]

\[b = \frac{1}{m}\sum_{i=1}^m (y_i-wx_i) \tag{2.7}
\]

其中 \(\overline{x} = \frac{1}{m}\sum\limits_{i=1}^m x_i\) 为 \(x\) 的均值。

或

\[方差\ var(x) = \frac{\sum\limits_{i=1}^m(x_i-\bar{x})^2}{m-1}
\]

\[协方差\ cov(x,y) = \frac{\sum_\limits{i=1}^m (x_i-\overline{x})(y_i-\overline{y})}{n-1}
\]

\[w = \frac{cov(x,y)}{var(x)} = \frac{\sum_\limits{i=1}^m (x_i-\overline{x})(y_i-\overline{y})}{\sum\limits_{i=1}^m (x_i-\overline{x})^2}
\]

\[b = \bar{y} - w\bar{x}
\]

下面使用 Python 计算 \(w\) 和 \(b\) 的值：

# 法一：
# w = np.sum(price * (dia - np.mean(dia))) / (np.sum(dia**2) - (1/dia.size) * (np.sum(dia))**2)
# b = (1 / dia.size) * np.sum(price - w * dia)

#法二：
variance = np.var(dia, ddof=1)  # 计算方差，doff为贝塞尔（无偏估计）校正系数
covariance = np.cov(dia, price)[0][1]  # 计算协方差
w = covariance / variance
b = np.mean(price) - w * np.mean(dia)

print("w = %f\nb = %f" % (w, b))

y_pred = w * dia + b

plt = runplt()
plt.plot(dia, price, 'k.')  # 样本点
plt.plot(dia, y_pred, 'b-')  # 手动求出的线性回归模型
plt.plot(X2, y2, 'g-.')  # 使用LinearRegression.fit()求出的模型
plt.show()

w = 0.976293
b = 1.965517

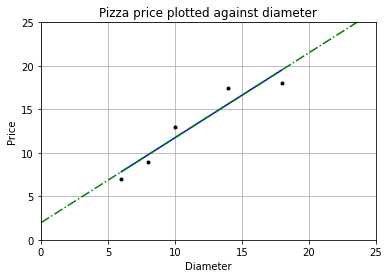
可以看到两条直线重合，我们求出的回归模型与使用库求出的回归模型相同。

3.2.2 功能封装

将上述代码封装成类：

class LinearRegression:
    """
    拟合一元线性回归模型

    Parameters
    ----------
    x : shape 为(样本个数,)的 numpy.array
        只有一个属性的数据集

    y : shape 为(样本个数,)的 numpy.array
        标记空间

    Returns
    -------
    self : 返回 self 的实例.
    """
    def __init__(self):
        self.w = None
        self.b = None

    def fit(self, x, y):
        variance = np.var(x, ddof=1)  # 计算方差，doff为贝塞尔（无偏估计）校正系数
        covariance = np.cov(x, y)[0][1]  # 计算协方差
        self.w = covariance / variance
        self.b = np.mean(y) - w * np.mean(x)
#         self.w = np.sum(y * (x - np.mean(x))) / (np.sum(x**2) - (1/x.size) * (np.sum(x))**2)
#         self.b = (1 / x.size) * np.sum(y - self.w * x)
        return self

    def predict(self, x):
        """
        使用该线性模型进行预测

        Parameters
        ----------
        x : 数值 或 shape 为(样本个数,)的 numpy.array
            属性值

        Returns
        -------
        C : 返回预测值
        """
        return self.w * x + self.b

使用：

# 创建并拟合模型
model = LinearRegression()
model.fit(dia, price)

x2 = np.array([0, 25])  # 取两个预测值
y2 = model.predict(x2)  # 进行预测
print(y2)  # 查看预测值

runplt()
plt.plot(dia, price, 'b.')
plt.plot(x2, y2, 'y-')  # 画出拟合
plt.show()

[ 1.96551724 26.37284483]

---

此文原创禁止转载，转载文章请联系博主并注明来源和出处，谢谢！

作者: Raina_RLN https://www.cnblogs.com/raina/