#Week3 Linear Regression with Multiple Variables

一、Multiple Features

这节课主要引入了一些记号，假设现在有n个特征，那么：



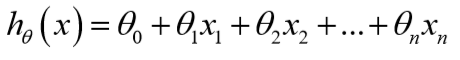
为了便于用矩阵处理，令\(x_0=1\)：



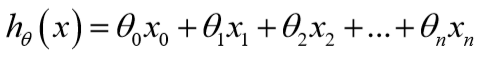
参数\(\theta\)是一个(n+1)*1维的向量，任一个训练样本也是(n+1)*1维的向量，故对于每个训练样本：\(h_\theta(x)=\theta^Tx\)。

二、Gradient Decent for Multiple Variables

类似地，定义代价函数：



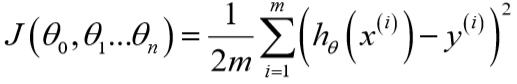
同时更新参数直到\(J\)收敛：

\[\theta_j:=\theta_j-\alpha \frac{1}{m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}
\]

三、Feature Scaling

这些特征的值如果有着近似的尺度，那么梯度下降会收敛得更快，其实就是归一化。

Andrew建议将特征的值缩放到[-1,1]之间：

\[x_i=\frac{x_i-u_i}{s_i}，u_i是平均值，s_i可以取max-min或者取标准差
\]

四、Learning Rate

1、梯度下降收敛所需的迭代次数是不确定的，可以通过绘制迭代次数与\(J\)的图来预测何时收敛；也可以通过代价函数的变化是否小于某个阈值来判断。

2、学习率一般可以尝试0.001，0.003，0.01，0.03，0.1，0.3，1...

五、Features and Polynomial Regression

线性回归有时候并不适用，有时需要多项式回归。

多项式回归可以转化为线性回归。

六、Normal Equation

正规方程通过直接求导，使得导数为0，进而求得\(\theta\)的解析解，使得\(J\)最小，而不需要像梯度下降那样迭代。



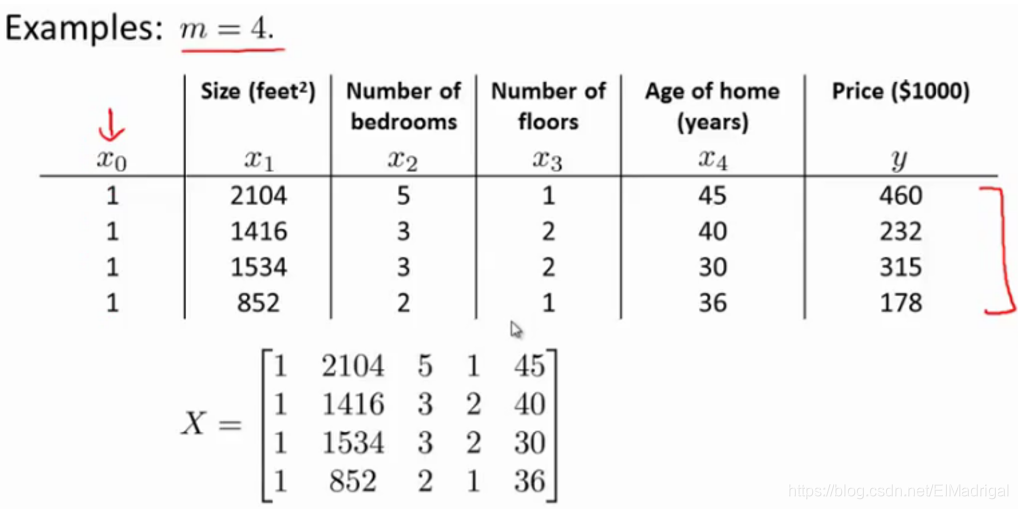
X是m*(n+1)特征矩阵，y是m*1向量，由图容易得出：

\(y=X\theta\)（这公式显然是错的。。。\(y\)只是采集到的标签），解出\(\theta=X^{-1}y\)（所以结论也是错的），这样得到的\(\theta\)显然不能使得损失函数最小。

课程里写成了\(\theta=(X^TX)^{-1}X^Ty\)，详细推导是通过对代价函数求导得到的。这个公式不能化简为\(\theta=X^{-1}y\)，因为只有\(X^T\)和\(X\)都可逆，才有\((X^TX)^{-1}=X^{-1}(X^T)^{-1}\)。

两种算法的比较：



正规方程只适用于线性模型，而且不需要Feature Scaling。