二叉树（3）AVL 树

封装基于 BinaryTreeOperations 的 AVL 树（一种自平衡的二叉查找树）。

除了提供 BinaryTreeOperations 中的部分基础接口外，增加按键的插入 和 按键或节点指针的删除操作。

在阅读本文前，您应该先了解二叉树中的旋转是怎么回事（相关文章很多且简单，笔者不再赘述）。

一、节点定义：

struct Node
{
    _Ty key;
    ;
    Node* left = nullptr;
    Node* right = nullptr;
    Node* parent = nullptr;
    Node(const _Ty& _key) :key(_key) {}
};

二、AVL 树的规则：

　　任何节点的两个子树最大高度差为 1。

根据 AVL 树的规则，可见在插入和删除节点后，可能会打破 AVL 树的平衡，因此在插入和删除时应进行调整，使得 AVL 树能够自平衡。

因此在节点定义中加入平衡因子 bf 用于记录节点的平衡状态。

注：bf == 0 时，节点左右子树等高；bf == -1 时，左子树高一层；bf == 1 时，右子树高一层。bf 绝对值大于 1 时应该进行调整。

调整时需要进行旋转，旋转规则（令失衡节点为 cur）：

　　① 左左_右旋：cur 左子树比右子树高两层（bf == -2）且 cur 的左子树 bf == -1 时：以 cur 右旋。

　　② 右右_左旋：cur 右子树比左子树高两层（bf == 2）且 cur 的左子树 bf == 1时：以 cur 左旋。

　　③ 左右_左右旋：cur 左子树比右子树高两层（bf == -2）且 cur 的左子树 bf == 1时：先以 cur 的左孩子左旋，再以 cur 右旋。

　　④ 右左_右左旋：cur 右子树比左子树高两层（bf == 2）且 cur 的左子树 bf == -1时：先以 cur 的右孩子右旋，再以 cur 左旋。

　　注意 bf 值的含义，左子树高还是右子树高或者等高。

单旋转方法已经在 BinaryTreeOperations.h 中给出。

三、现对旋转（单旋转和双旋转）后相关节点的平衡因子 bf 的变化进行说明（很多教程并未明确提出 导致读者不能明确 bf 的变化）。

　　一、以左旋为例（单旋），右旋与左旋类似。

　　二、以 右左旋为例（双旋），左右旋与右左旋类似。

　　先看 一，与下图结合看（假设应该调整的节点是 X）：

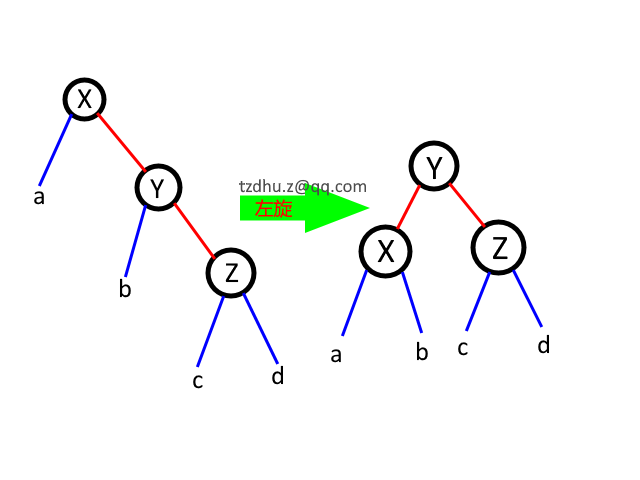
　　发现：

　　① Z 节点孩子未发生变动，因此 Z 节点的平衡因子不需要改变。

　　② 若 a 为空，则 b,c,d 必定为空（看 AVL 树的规则），因此，X,Y 的平衡因子均应该置零。(此时插入的节点为 Z)。

　　③ 若 a 不为空，则 b 一定不为空，c,d 一定其一为空，另一个不为空。(此时插入的节点为 c,d 之一，另一个为空)。可见，X,Y 节点任然平衡，平衡因子应置零。

　　再看 二，与下图结合看（假设应该调整的节点是 X）：

　　发现：

　　① Z 一定平衡（见下分析），其平衡因子 bf 应置零。

　　② 若 a 为空，则 b,c,d 必定为空（看 AVL 树的规则），X,Y,Z 的平衡因子均应该置零。(此时插入的节点为 Z)。

　　③ 若 a 不为空，则 b 一定不为空，c,d 一定其一为空，另一个不为空。(此时插入的节点为 c,d 之一，另一个为空)。

　　　　1）若插入为 c，则 X 平衡，其 bf 应置零，Y 右子树高，其 bf 应置 1。

　　　　2）若插入为 d，则 X 左子树高，其 bf 应置 -1，Y 平衡，其 bf 应置零。

　　至此，单旋双旋 旋转后旋转因子的变化说明清楚（调用 BinaryTreeOperations.h 中的旋转方法后应修改相关节点的 bf）。

四、插入操作：

　　可知，新插入的节点（令为 cur）必定是空位置，令插入后其父亲节点为 par（考虑成功插入的情况，只有成功插入才可能打破平衡）。

　　插入后的自平衡很简单，首先要知道，插入后 par 一定不会失去平衡（不用解释吧）。

　　插入后分为两种情况讨论即可（令 par 的父亲节点为 gpa，也就是新加节点的祖父节点）：

　　　　一、par 有两个孩子。

　　　　二、par 只有一个孩子。

　　先看 一：par 有两个孩子，说明 cur 的插入没有给 par 或者 par 的祖先带来高度变化（没有新加层），此时直接返回即可。

　　再看二：par 只有一个孩子，说明 cur 的插入带来了高度变化，可能需要调整，此时应该怎能做呢？

　　　　① 先根据 par 和 gpa 的关系（即 par 是 gpa 的左孩子还是右孩子）来更新 gpa 的 bf。（默认插入时已经对 par 的平衡因子进行更新）

　　　　　　注：如何更新 par 和 gpa 的平衡因子不用说吧？（看是左孩子还是右孩子，右孩子 则 bf 自增，左孩子 则 bf 自减）。

　　　　② 根据 gpa 的平衡因子判断是否需要调整（即是否需要旋转）。

　　　　　　1）gpa 不需要旋转，则 par,gpa 分别指向各自父节点，继续 ① 操作，直到 2）或者 gpa 为空。

　　　　　　2）gpa 要旋转，则根据 par,gpa 的 bf 判断旋转方法进行调整，然后返回即可（请看上文 旋转规则）。

　　　　　　注：2）之后需要继续向上操作吗？（当然不需要！gpa 旋转后，对 gpa 的祖先而言没有高度的增加和减小）。

　　　　注意插入空树的情况。

　　至此，插入操作讲解完成，后序进行删除操作讲解，这会比插入操作稍加困难。

五、删除操作：

　　删除操作会比插入操作稍加复杂，下面先分析其原因所在（这里令 待删除节点为 cur，其父节点为 par）。

　　注：红黑树亦是如此，RBTree 的 删除比 AVLTree 的删除更加复杂，所以对于 AVLTree 的删除不用慌。

　　① 插入时， 新插入节点的 父亲节点 在插入前 一定：没有孩子 或 有一个孩子（该孩子一定没有孩子），而删除时 cur 可能没有孩子或有一个或两个孩子。

　　② 删除时有无孩子都需要判断是否 cur 是根节点。

　　③ 应该如何删除 cur 且如何判断是否调整。

　　针对上述问题，我们可将其简化。

　　　　① 删除节点是否为根节点的问题比较简单，只需做一下判断即可，后文不讨论该情况。

　　　　② 删除节点有两个孩子时：如二叉查找树一般，用后继节点代替并调用函数自身去删除后继结点（也可用前驱节点代替）。

　　　　③ 删除节点没有孩子。

　　　　④ 删除节点只有一个孩子。

　　　　注：② 中的后继结点（或前驱节点）一定属于 ③ 或 ④ 情况。

　　因此，将重点讨论 ③ ④ 情况。

　　即：

　　一、删除节点没有孩子（是叶子节点）。

　　二、删除节点只有一个孩子。

　　注：令 cur 为待删除节点，par 为其父亲节点，gpa 为 par 的父亲节点。

　　先看 一（cur 是叶子节点）：

　　　　① 若 cur 不存在兄弟节点，则删除 cur 会造成高度变化，gpa 是第一个可能失衡的节点（不用图也能想清楚吧）。

　　　　② 若 cur 存在兄弟节点，则 par 可能失衡（比如 par 右子树深度为2，左子树深度为一，删除左子树会失衡）。

　　　　OK，既然知道第一个可能失去平衡的节点，那只需要检测并调整就好了。

　　注意：什么情况需要继续向根节点回溯呢？即：通过旋转操作后 需要继续向上 还是 没有旋转操作 才需要继续向上？

　　当然是：par 经过旋转后才需要继续向上，若 par 不需要旋转，则 gpa 没有发生左右子树高度差变化，反之，par 经过旋转后 gpa 对应 par 子树的高度减小，则可能失衡。

　　所以 par 为经旋转是退出循环的条件。

　　继续回溯时，注意改变父节点的 bf。

　　再看 二（cur 只有一个孩子）：

　　　　① cur 只有一个孩子，则该孩子一定没有孩子（否则 cur 不是平衡的）。

　　　　② 删除 cur，par 在 cur 的子树上高度一定减小，par 则有可能失衡，即 par 是第一个可能失衡点。

　　　　③ 删除 cur 时，用 cur 的孩子替代 cur 并删除 cur 的孩子，然后从 par 开始回溯判断是否需要调整，退出循环条件与前文一致。

　　至此，删除说明到此为止，AVL 树的说明也到此为止，最后给出示例代码。

测试代码 main.cpp：

#include <iostream>
#include "AVLTree.h"
 
using std::cout;
using std::endl;
 
int main()
{
    AVLTree<int> avl;
 
    auto Add = [&avl](int _key)
    {
        cout << "Add " << _key << ":" << endl;
        avl.insert(_key);
        avl.levelTraversal();
        cout << endl << "size: " << avl.size() << "  level: " << avl.level() << endl << endl;
    };
    auto il = { , , , , , ,  };
    for (auto& x : il) Add(x);
    auto Del = [&avl](int _key)
    {
        cout << "Del " << _key << ":" << endl;
        avl.erase(_key);
        avl.levelTraversal();
        cout << endl << "size: " << avl.size() << "  level: " << avl.level() << endl << endl;
    };
    Del(); Del(); Del();
 
    ;
}

头文件 AVLTree.h：

#pragma once
#ifndef __AVLTREE_H__
#define __AVLTREE_H__
 
#include"BinaryTreeOperations.h"
template<typename _Ty>
class AVLTree
{
private:
    struct Node
    {
        _Ty key;
        ;
        Node* left = nullptr;
        Node* right = nullptr;
        Node* parent = nullptr;
        Node(const _Ty& _key) :key(_key) {}
    };
 
public:
    AVLTree() = default;
    ~AVLTree() { BTO::clear(root); size_n = ; }
    ; }
 
    void preorderTraversal() { BTO::preorderTraversal(root, drawData); }
    void inorderTraversal() { BTO::inorderTraversal(root, drawData); }
    void postorderTraversal() { BTO::postorderTraversal(root, drawData); }
    void iterativePreorderTraversal() { BTO::iterativePreorderTraversal(root, drawData); }
    void iterativeInorderTraversal() { BTO::iterativeInorderTraversal(root, drawData); }
    void iterativePostorderTraversal() { BTO::iterativePostorderTraversal(root, drawData); }
    void levelTraversal() { BTO::levelTraversal(root, drawData); }
 
    Node* find(const _Ty& _key) { return BTO::find(root, _key); }
    Node* iterativeFind(const _Ty& _key) { return BTO::iterativeFind(root, _key); }
    Node* findMaximum() { return BTO::findMaximum(root); }
    Node* findMinimum() { return BTO::findMinimum(root); }
    size_t level() { return BTO::getLevel(root); }
    size_t size() const { return size_n; }
 
    void insert(const _Ty&);
    bool erase(const _Ty&);
    void erase(Node*);
 
private:
    void LL_R(Node*);
    void RR_L(Node*);
    void LR_LR(Node*);
    void RL_RL(Node*);
    static void drawData(const Node* _node) { std::cout << _node->key << " "; }
 
private:
    size_t size_n = ;
    Node* root = nullptr;
};
 
template<typename _Ty>
void AVLTree<_Ty>::LL_R(Node* _node)
{
    _node = BTO::rightRotate(_node);
    _node->bf = _node->right->bf = ;
    if (_node->parent == nullptr) root = _node;
}
 
template<typename _Ty>
void AVLTree<_Ty>::RR_L(Node* _node)
{
    _node = BTO::leftRotate(_node);
    _node->bf = _node->left->bf = ;
    if (_node->parent == nullptr) root = _node;
}
 
template<typename _Ty>
void AVLTree<_Ty>::LR_LR(Node* _node)
{
    BTO::leftRotate(_node->left);
    _node = BTO::rightRotate(_node);
    if (_node->right->right == nullptr)
        _node->left->bf = _node->right->bf = ;
    else
    {
        if (_node->right->left == nullptr)
        {
            _node->right->bf = ;
            _node->left->bf = ;
        }
        else
        {
            _node->left->bf = ;
            _node->right->bf = -;
        }
    }
    _node->bf = ;
    if (_node->parent == nullptr) root = _node;
}
 
template<typename _Ty>
void AVLTree<_Ty>::RL_RL(Node* _node)
{
    BTO::rightRotate(_node->right);
    _node = BTO::leftRotate(_node);
    if (_node->left->left == nullptr)
        _node->left->bf = _node->right->bf = ;
    else
    {
        if (_node->left->right == nullptr)
        {
            _node->left->bf = -;
            _node->right->bf = ;
        }
        else
        {
            _node->left->bf = ;
            _node->right->bf = ;
        }
    }
    _node->bf = ;
    if (_node->parent == nullptr) root = _node;
}
 
template<typename _Ty>
void AVLTree<_Ty>::insert(const _Ty& _key)
{
    auto ret = BTO::insert(root, _key);
    if (ret.second) ++size_n;
    else return;
    auto temp = ret.first;
    if (temp->parent == nullptr) return;
 
    ;
    ;
    temp = temp->parent;
    if (temp->left != nullptr && temp->right != nullptr) return;
 
    Node* pa = temp->parent;
    while (pa != nullptr)
    {
        if (temp == pa->left)
            pa->bf += -;
        else
            pa->bf += ;
        )
        {
            ) LL_R(pa);
            else LR_LR(pa);
            break;
        }
        )
        {
            ) RL_RL(pa);
            else RR_L(pa);
            break;
        }
        temp = pa;
        pa = pa->parent;
    }
}
 
template<typename _Ty>
bool AVLTree<_Ty>::erase(const _Ty& _key)
{
    bool succeed = false;
    Node* del = BTO::find(root, _key);
    if (del != nullptr)
    {
        erase(del);
        succeed = true;
    }
    return succeed;
}
 
template<typename _Ty>
void AVLTree<_Ty>::erase(Node* _node)
{
    if (_node == nullptr) return;
    --size_n;
    Node* pa = nullptr;
    Node* temp = nullptr;
    if (_node->left == nullptr && _node->right == nullptr)
    {
        if (_node == root)
        {
            root = nullptr;
            delete _node;
            return;
        }
        if (_node == _node->parent->left)
        {
            _node->parent->left = nullptr;
            _node->parent->bf += ;
            temp = _node->parent->right;
        }
        else
        {
            _node->parent->right = nullptr;
            _node->parent->bf += -;
            temp = _node->parent->left;
        }
        pa = _node->parent;
        delete _node;
    }
    else if (!(_node->left != nullptr && _node->right != nullptr))
    {
        if (_node->parent == nullptr)
        {
            if (_node->left != nullptr) root = _node->left;
            else root = _node->right;
            root->parent = nullptr;
            delete _node;
            return;
        }
        if (_node == _node->parent->left)
        {
            _node->parent->left = _node->left == nullptr ? _node->right : _node->left;
            if (_node->left != nullptr) _node->left->parent = _node->parent;
            else _node->right->parent = _node->parent;
            _node->parent->bf += ;
            temp = _node->parent->right;
        }
        else
        {
            _node->parent->right = _node->left == nullptr ? _node->right : _node->left;
            if (_node->left != nullptr) _node->left->parent = _node->parent;
            else _node->right->parent = _node->parent;
            _node->parent->bf += -;
            temp = _node->parent->left;
        }
        pa = _node->parent;
        delete _node;
    }
    else
    {
        Node* de = BTO::findMinimum(_node->right);
        _node->key = de->key;
        ++size_n;
        erase(de);
    }
    )
    {
        temp = pa;
        pa = pa->parent;
        if (pa != nullptr)
        {
            if (temp == pa->left)
            {
                temp = pa->right;
                pa->bf += ;
            }
            else
            {
                temp = pa->left;
                pa->bf += -;
            }
        }
    }
    while (pa != nullptr)
    {
        )
        {
             || temp->bf == ) LL_R(pa);
            else LR_LR(pa);
        }
        )
        {
            ) RL_RL(pa);
            else RR_L(pa);
        }
        else break;
         : ;
        pa = temp->parent;
        if (pa != nullptr)
        {
            if (isLeft)
            {
                temp = pa->left;
                pa->bf += -;
            }
            else
            {
                temp = pa->right;
                pa->bf += ;
            }
        }
    }
}
 
#endif // !__AVLTREE_H__