20181026_队测_Brick Game
题目描述
给出一个\(n\)行\(m\)列的矩阵,矩阵中每个格子有一个非负整数,现在要求你去除其中的个格子,使得剩下的格子中的数的总和最大。另外,去除\(k\)个格子后,剩下的格子必须满足以下几个性质:
1.连续性:同一行的格子是连续的,也就是说,剩下的格子不会出现同一行有两个分离的连续段的情况。
2.支撑性:除了底行以外,在其他剩下的行中保留的连续格子段,至少有一个格子与它下一行某个保留的格子处于同一列中。
3.保底性:最后一行至少保留一个格子。
输入输出格式
输入格式
第一行有三个整数\(n,m,k(1\leq n,m\leq 64,max(nm-64,0)\leq k<nm)\),表示矩阵的大小以及去除格子的个数。
接下来有\(n\)行,每\(m\)行个非负整数,表示矩阵的元素。矩阵中每个元素的值不超过\(32767\)
输出格式
一个整数,表示去除\(k\)个格子后,剩下的格子中的数的总和的最大值。
样例
INPUT
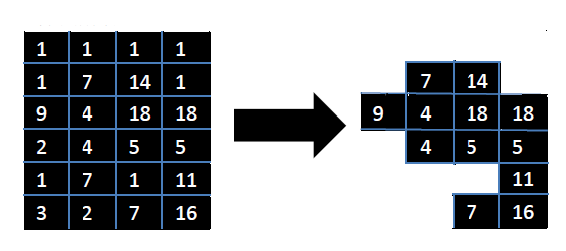
6 4 12
1 1 1 1
1 7 14 1
9 4 18 18
2 4 5 5
1 7 1 11
3 2 7 16
OUTPUT
118
HINT
对于\(30\text %\)的数据,\(n,m\leq 5\)
对于\(60\text %\)的数据,\(n,m\leq 10\)
对于\(100\text %\)的数据,\(n,m\leq 64\)
SOLUTION
dp
首先观察题目所给的三个性质:连续性,支撑性,保底性。这三个性质相当于在提示我们dp方程的转移方式。
- 连续性:我们的转移应该是从某层的某个区间段转移到其相邻层的某个区间段。
- 支撑性:转移应该发生在点\((i,j)\)所在的某个区间与点\((i-1,j)\)所在的某个区间之中。
- 保底性:为了使最后一行一定有方格,可以考虑从上往下转移,如此上层可以出现整层不选的情况,而下层则不会。
由上面对性质的分析我们也可以看出转移过程有几个关键字:①区间;②点;而本题又要求删去\(k\)个方格于是又有③方格数;
不难得出一个简单一点的想法,\(dp\)数组记四维:\(dp[i][l][r][k]\)表示取第\(i\)行的区间\([l,r]\)选择了\(k\)个的情况。但是,如此设置\(dp\)数组会使时间复杂度达到\(O(n^6)\)的级别(枚举\(i\),枚举本层\(l,r\),枚举\(k\),枚举上层的\(l‘,r’\)),虽然本题的数据范围非常小,\(n\leq 64\),按照这个时间复杂度,枚举量仍然能够达到\(2^{36}\)(虽然有很多种情况是废弃的)所以这种\(dp\)方式只能用来暴力拿部分分。
转移关键字应该是没有错的,那么如何优化呢?
考虑区间的性质,区间可以通过一个端点+区间长度+从该点出发表示该区间的延伸方向表示,由于方向只可能有两种(向左或向右)那么我们一样可以通过枚举端点和区间长度来得到一个区间。
而区间长度其实只是用来计算方格内数值的,所以还有\(k\)个方格可选时,“区间长度为\(len\)”这个信息其实是用来辅助计算\(k-len\)个可选时的最优方案的。换而言之,就是计算到最后我们并不关心这个答案是从多长的区间转移来的,所以可以优化掉这一维,区间长度\(len\)值作为一个中间值不被记录在\(dp\)数组里。
没有区间长度,怎么判断支撑性呢?别忘了支撑性可以通过点与点来判断,我们把区间转化为一个个关键点来考虑。所谓关键点就是某个区间的某个端点,接下来我们讨论的就是这个问题。
我们记两个数组\(lft[i][j][k],rgt[i][j][k]\),表示右/左端点为点\((i,j)\)的某区间,而转移到此时,剩余可选的方格数为\(k\)。
因为为了优化复杂度,我们把三维的区间改成了二维的关键点,那么相应地,转移方面就要稍微复杂一些。
同层转移:对于\(lft[i][j][k]\)显然可以看作由\(lft[i][j-1][k-1]\)加上点\((i,j)\)的值构成的答案。
上下层关键点转移:很两个关键点上下相邻的区间一定是合法的,我们就可以通过枚举本层区间长度\(len\),通过已经枚举而已知的\(k\)算出上层的状态进行转移。这是“关键-->关键”。
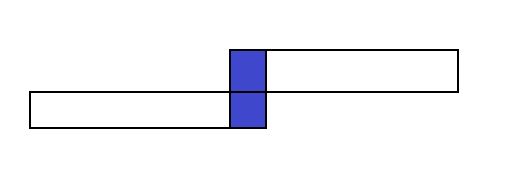
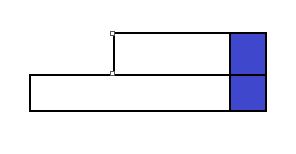
上层非关键点转移:而对于那种本层的关键点的上层对应点不是关键点的情况,其实也可以转化成关键点之间的转移来做,只要在已知左端点\(p\)的区间的左边再加上一段区间就可以构成\(p\)不是关键点的区间,(而区间长度恰巧也要枚举\(len\),可以把转移2和转移3一起在\(len\)的循环中完成)这么做就可以做到“非关键-->关键”。

而由于我们会做同层转移所以转移3在本层只取一个点也不会遗漏情况。
如此一来时间复杂度自然就降到\(O(n^4)\)了。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <cstdlib>
using namespace std;
typedef long long LL;
#define Max(a,b) ((a>b)?a:b)
#define Min(a,b) ((a<b)?a:b)
const int N=70;
const int INF=1000010000;
int n,m,K,lft[N][N][N],rgt[N][N][N],sum[N][N];
short sq[N][N];
inline int read(){
int x=0,f=1;char ch=getchar();
while (ch<'0'||ch>'9') {if (ch=='-') f=-1;ch=getchar();}
while (ch>='0'&&ch<='9') {x=x*10+ch-48;ch=getchar();}
return x*f;}
int main(){
int i,j;
n=read();m=read();K=read();K=n*m-K;
memset(lft,0,sizeof(lft));memset(rgt,0,sizeof(rgt));memset(sum,0,sizeof(sum));
for (i=1;i<=n;++i)
for (j=1;j<=m;++j) sq[i][j]=read();
for (i=1;i<=n;++i)
for (j=1;j<=m;++j) sum[i][j]=sum[i][j-1]+sq[i][j];
for (int k=1;k<=K;++k){
for (i=1;i<=n;++i){
for (j=1;j<=m;++j){
int &L=lft[i][j][k];int &R=rgt[i][j][k];
if (k==1) {L=R=sq[i][j];continue;}
L=R=-INF;
if (j>1) L=lft[i][j-1][k-1]+sq[i][j];
if (j<m) R=rgt[i][j+1][k-1]+sq[i][j];
if (i==1) continue;
for (int len=1;len<=k;++len){
int remn=k-len;
if (len<=j) {L=Max(L,Max(rgt[i-1][j][remn],lft[i-1][j][remn])+sum[i][j]-sum[i][j-len]);}
if ((len+j-1)<=m) {R=Max(R,Max(rgt[i-1][j][remn],lft[i-1][j][remn])+sum[i][j+len-1]-sum[i][j-1]);}
if ((len<=j)&&remn){
int now=rgt[i-1][j][remn]+sum[i-1][j-1]-sum[i-1][j-len]+sq[i][j];
L=Max(L,now);R=Max(R,now);}
if (((len+j-1)<=m)&&remn){
int now=lft[i-1][j][remn]+sum[i-1][j+len-1]-sum[i-1][j]+sq[i][j];
L=Max(L,now);R=Max(R,now);}
}
}
}
}
int ans=0;for (i=1;i<=m;++i) {ans=Max(ans,Max(lft[n][i][K],rgt[n][i][K]));printf("");}
printf("%d\n",ans);
return 0;
}
20181026_队测_Brick Game的更多相关文章
- OI队测题解:
Test 17 T1: 题目大意: 喵星系有n个星球,标号为1到n,星球以及星球间的航线形成一棵树. 所有星球间的双向航线的长度都为1.小昕要在若干个星球建矿石仓库,设立每个仓库的费用为K.对于未 ...
- Test 17
BZ OI 队测 T1: 题目大意: 喵星系有n个星球,标号为1到n,星球以及星球间的航线形成一棵树. 所有星球间的双向航线的长度都为1.小昕要在若干个星球建矿石仓库,设立每个仓库的费用为K.对于未设 ...
- cogs:1619. [HEOI2012]采花/luogu P2056
1619. [HEOI2012]采花 ★★☆ 输入文件:1flower.in 输出文件:1flower.out 简单对比时间限制:5 s 内存限制:128 MB [题目描述] 萧薰儿是 ...
- bzoj 5216 [Lydsy2017省队十连测]公路建设 线段树维护 最小生成树
[Lydsy2017省队十连测]公路建设 Time Limit: 20 Sec Memory Limit: 512 MBSubmit: 93 Solved: 53[Submit][Status][ ...
- bzoj 5216: [Lydsy2017省队十连测]公路建设
5216: [Lydsy2017省队十连测]公路建设 Time Limit: 20 Sec Memory Limit: 512 MBSubmit: 66 Solved: 37[Submit][St ...
- Lydsy2017省队十连测
5215: [Lydsy2017省队十连测]商店购物 可能FFT学傻了,第一反应是前面300*300背包,后面FFT... 实际上前面背包,后面组合数即可.只是这是一道卡常题,需要注意常数.. //A ...
- 2018.09.26 bzoj5218: [Lydsy2017省队十连测]友好城市(回滚莫队)
传送门 比较简单的一道回滚莫队吧. 每次询问用bitset优化kosaraju统计答案. 就是有点难调. 然后向dzyo学长学习了回滚莫队的一种简洁的实现方式,就是直接建立一个sqrt(m)∗sqrt ...
- bzoj 5218: [Lydsy2017省队十连测]友好城市
题意: 这题显然直接tarjan是做不了的. 这里安利另一个求SCC的算法Kosaraju,学习的话可以见这篇博客 于是结合莫队,我们有了个暴力. 发现主要瓶颈是dfs过程中找最小的未经过的点,我们用 ...
- 【河北省队互测】 gcd BZOJ 2818
Description 给定整数N,求1<=x,y<=N且Gcd(x,y)为素数的 数对(x,y)有多少对. Input 一个整数N Output 如题 Sample Input 4 Sa ...
随机推荐
- leetcode中的sql
1 组合两张表 组合两张表, 题目很简单, 主要考察JOIN语法的使用.唯一需要注意的一点, 是题目中的这句话, "无论 person 是否有地址信息".说明即使Person表, ...
- 吴裕雄--天生自然 PHP开发学习:高级
<?php echo date("Y/m/d") . "<br>"; echo date("Y.m.d") . " ...
- 基于redis实现锁控制
多数据源 数据源1为锁控制,数据源2自定义,可用于存储. 锁:当出现并发的时候为了保证数据的一致性,不会出现并发问题,假设,用户1修改一条信息,用户2也同时修改,会按照顺序覆盖自修改的值,为了避免这种
- no.2淘宝架构背后——零售业务中台架构设计探讨及实践读后感
2017年8月12日,袋鼠云首席架构师正风在“网易博学实践日:大数据与人工智能技术大会”进行<淘宝架构演进背后——零售业务中台架构设计探讨及实践>演讲分享.传统零售行业如何选择应对新经济模 ...
- vue-cli3解决跨域问题
在 vue.config.js里面配置 devServer: { proxy: { '/': { // search为转发路径 target: 'http://www.baidu.com', // 目 ...
- 17.3.20---python的变量作用域
1---变量的作用域 在Python程序中创建.改变.查找变量名时,都是在一个保存变量名的空间中进行,我们称之为命名空间,也被称之为作用域.Python的作用域是静态的,在源代码中变量名被赋值的位置决 ...
- day06-初识Vuetify框架UI框架和使用域名访问本地项目
本项目的笔记和资料的Download,请点击这一句话自行获取. day01-springboot(理论篇) :day01-springboot(实践篇) day02-springcloud(理论篇一) ...
- linux下别名的设定
命令别名设定功能: (alias)假如我需要知道这个目录底下的所有文件 (包含隐藏档) 及所有的文件属性,那么我就必须要下达『 ls -al 』这样的指令串,比较麻烦,我们可以为其设定别名为lm al ...
- 基于邻接表的长度为k的简单路径的求解
描述 一个连通图采用邻接表作为存储结构.设计一个算法,判断无向图中任意给定的两点是否存在一条长度为k的简单路径. 输入 多组数据,每组m+3数据行.第一行有两个数字n,m和k,代表有n个顶点,m条边和 ...
- MFC的cstring判断是否存在中文字符
bool IsChinese(CString Cstr) { int nLen = Cstr.GetLength(); unsigned char ch1, ch2; for (int i = 0; ...
