BZOJ3073 Journeys - 线段树优化建边

传送门

题意：

Seter建造了一个很大的星球，他准备建造N个国家和无数双向道路。N个国家很快建造好了，用1..N编号，但是他发现道路实在太多了，他要一条条建简直是不可能的！于是他以如下方式建造道路：(a,b),(c,d)表示，对于任意两个国家x,y，如果a<=x<=b,c<=y<=d，那么在xy之间建造一条道路。Seter保证一条道路不会修建两次，也保证不会有一个国家与自己之间有道路。

Seter好不容易建好了所有道路，他现在在位于P号的首都。Seter想知道P号国家到任意一个国家最少需要经过几条道路。当然，Seter保证P号国家能到任意一个国家。

分析：

直接建边空间会达到\(n^2m\)。于是可以线段树来优化：两颗线段树：进树，出树。（下面括号代表边权）

进树： 从父亲向儿子连边(0)，表示能达到该区间就能达到该区间的子区间。

出树：从儿子向父亲连边(0)，表示能从该区间出发就能从该区间的父区间出发。

两树之间：

• 进树向出树的对应区间连边(0)，表示到达该区间后，还能从该区间继续出发。
• 对于给出的边，从出树中找到对应区间，向新建的超级点连边(0)，从超级点向进树的对应区间连边(1)，由于是无向边，要连加两次。

例如5个节点中连边[2, 3] <----> [4, 5]（此处就只连单向边示意）：

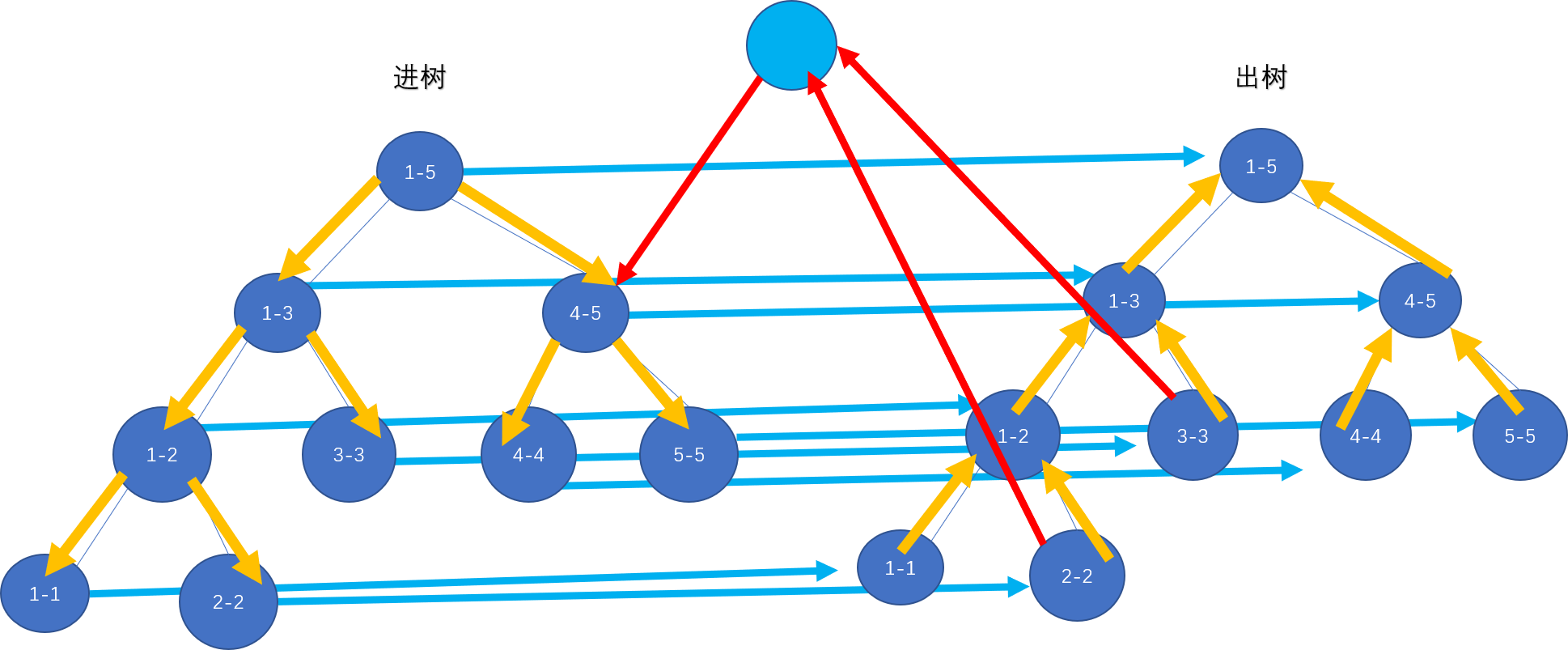
最后起点直接从出树向入树连边（因为根本不用走）。

剩下的就是dijsktra，答案就是进树的叶子节点距离。

code

#include<bits/stdc++.h>
using namespace std;
namespace IO {
	template<typename T>
	inline void read(T &x) {
		T i = 0, f = 1;
		char ch = getchar();
		for(; (ch < '0' || ch > '9') && ch != '-'; ch = getchar());
		if(ch == '-') f = -1, ch = getchar();
		for(; ch >= '0' && ch <= '9'; ch = getchar()) i = (i << 3) + (i << 1) + (ch - '0');
		x = i * f;
	}
	template<typename T>
	inline void wr(T x) {
		if(x < 0) putchar('-'), x = -x;
		if(x > 9) wr(x / 10);
		putchar(x % 10 + '0');
	}
} using namespace IO;

const int N = 5e5 + 50, M = 1e5 + 50, OO = 0x3f3f3f3f;
int n, m, p, dis[N * 10];
typedef pair<int, int> P;
vector<P> G[N * 10];
int tot, SuperPoint;
priority_queue<P, vector<P>, greater<P> > que;
bool vst[N * 10];

inline void addEdge(int u, int v, int c){
	G[u].push_back(P(v, c));
}
struct SegTree{
	int num[N * 4];
	inline void Build(int k, int l, int r, int type){
		num[k] = ++tot;
		if(l == r) return;
		int mid = l + r >> 1, lc = k << 1 , rc = k << 1 | 1;
		Build(lc, l, mid, type), type == 1 ? addEdge(num[lc], num[k], 0) : addEdge(num[k], num[lc], 0);
		Build(rc, mid + 1, r, type), type == 1 ? addEdge(num[rc], num[k], 0) : addEdge(num[k], num[rc], 0);
	}
	inline void BuildEdge(int k, int l, int r, int x, int y, int v, int type){
		if(x <= l && r <= y) {
			type == 1 ? addEdge(num[k], SuperPoint, v) : addEdge(SuperPoint, num[k], v);
			return;
		}
		int mid = l + r >> 1, lc = k << 1 , rc = k << 1 | 1;
		if(x <= mid) BuildEdge(lc, l, mid, x, y, v, type);
		if(y > mid) BuildEdge(rc, mid + 1, r, x, y, v, type);
	}
	inline int getNum(int k, int l, int r, int pp){
		if(l == r) return num[k];
		int mid = l + r >> 1, lc = k << 1 , rc = k << 1 | 1;
		if(pp <= mid) return getNum(lc, l, mid, pp);
		else return getNum(rc, mid + 1, r, pp);
	}
}SegIn, SegOut;
int debug[N * 18];
inline void DJ(int p){
	memset(dis, 0x3f, sizeof dis);
	dis[p] = 0;
	que.push(P(0, p));
	while(!que.empty()){
		P t = que.top();que.pop();
		int u = t.second;
		if(vst[u]) continue;
		vst[u] = true;
		for(int e = G[u].size() - 1; e >= 0; e--){
			int v = G[u][e].first;
//			cout<<u<<"-------->"<<v<<endl;
			if(!vst[v] && dis[v] > dis[u] + G[u][e].second){
				dis[v] = dis[u] + G[u][e].second;
				debug[v] = u;
				que.push(P(dis[v], v));
			}
		}
//		cout<<endl;
	}
}

inline void BuildEdgeBet(int k, int l, int r){
	addEdge(SegIn.num[k], SegOut.num[k], 0);
	if(l == r) return;
	int mid = l + r >> 1, lc = k << 1 , rc = k << 1 | 1;
	BuildEdgeBet(lc, l, mid);
	BuildEdgeBet(rc, mid + 1, r);
}

inline void getAns(int k, int l, int r){
	if(l == r){
		wr(dis[SegIn.num[k]]), putchar('\n');
		return;
	}
	int mid = l + r >> 1, lc = k << 1 , rc = k << 1 | 1;
	getAns(lc, l, mid);
	getAns(rc, mid + 1, r);
}

int main(){
	freopen("h.in" ,"r", stdin);
	freopen("h.out", "w", stdout);
	read(n), read(m), read(p);
	SegIn.Build(1, 1, n, 2);
	SegOut.Build(1, 1, n, 1);
	SuperPoint = tot;
	for(int i = 1; i <= m; i++){
		int a, b, c, d;
		read(a), read(b), read(c), read(d);
		SuperPoint++;
		SegOut.BuildEdge(1, 1, n, a, b, 0, 1);
		SegIn.BuildEdge(1, 1, n, c, d, 1, 2);
		SuperPoint++;
		SegOut.BuildEdge(1, 1, n, c, d, 0, 1);
		SegIn.BuildEdge(1, 1, n, a, b, 1, 2);

	}
	BuildEdgeBet(1, 1, n);
	int pos1 = SegOut.getNum(1, 1, n, p), pos2 = SegIn.getNum(1, 1, n, p);
	addEdge(pos1, pos2, 0);
//	for(int i = 0; i <= tot; i++){
//		cout<<i<<":";for(int j = 0; j < G[i].size(); j++) cout<<G[i][j].first<<" ";
//		cout<<endl;
//	}
	DJ(pos1);
	getAns(1, 1, n);
//	int now = SegIn.getNum(1, 1, n, 1);
//	do{
//		cout<<now<<"<-----";
//		now = debug[now];
//	}while(now);
	return 0;
}