GYM 100741A Queries(树状数组)

A. Queries

time limit per test

0.25 seconds

memory limit per test

64 megabytes

input

standard input

output

standard output

Mathematicians are interesting (sometimes, I would say, even crazy) people. For example, my friend, a mathematician, thinks that it is very fun to play with a sequence of integer numbers. He writes the sequence in a row. If he wants he increases one number of the sequence, sometimes it is more interesting to decrease it (do you know why?..) And he likes to add the numbers in the interval [l;r]. But showing that he is really cool he adds only numbers which are equal some mod (modulo m).

Guess what he asked me, when he knew that I am a programmer? Yep, indeed, he asked me to write a program which could process these queries (n is the length of the sequence):

• + p r It increases the number with index p by r. (, )

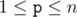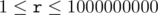  You have to output the number after the increase.

• - p r It decreases the number with index p by r. (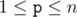, 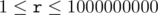) You must not decrease the number if it would become negative.

  You have to output the number after the decrease.

• s l r mod You have to output the sum of numbers in the interval 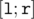 which are equal mod (modulo m). () ()

Input

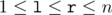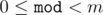The first line of each test case contains the number of elements of the sequence n and the number m. (1 ≤ n ≤ 10000) (1 ≤ m ≤ 10)

The second line contains n initial numbers of the sequence. (0 ≤ number ≤ 1000000000)

The third line of each test case contains the number of queries q (1 ≤ q ≤ 10000).

The following q lines contains the queries (one query per line).

Output

Output q lines - the answers to the queries.

Examples

input

3 4
1 2 3
3
s 1 3 2
+ 2 1
- 1 2

output

2
3
1

题意:
1个长度为n 的序列,q 次三种操作:
+ p r: 下标为p 的数加r.
- p r: 下表为p 的数减r.
s l r mod: 询问在模m(提前给出) 意义下[l,r] 之中有多少个数等于mod.

/*
10个树状数组 分别记录mod m为几的数个数
加减号做 询问时输出模数所在树状数组l~r个数即可
*/
#include<bits/stdc++.h>

#define N 10010
#define ll long long

using namespace std;

struct BIT
{
    ll c[N];
    int n;

    int lowbit(int x){return x&(-x);}

    void modify(int x,ll y){for(; x<=n; x+=lowbit(x)) c[x]+=y;}

    ll query(int x)
    {
        ll ret=;
        for(; x; x-=lowbit(x)) ret+=c[x];
        return ret;
    }

    ll query(int l,int r){return query(r)-query(l-);}
} bit[];

int n,m,T;
ll a[N];

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=;i<m;i++) bit[i].n=n;
    for(int i=;i<=n;i++)
    {
        scanf("%lld",&a[i]);
        bit[a[i]%m].modify(i,a[i]);
    }
    scanf("%d",&T);
    while(T--)
    {
        int x,y,z;
        char opt[];
        scanf("%s%d%d",opt,&x,&y);
        if(opt[]=='+')
        {
            bit[a[x]%m].modify(x,-a[x]);
            a[x]+=y;
            bit[a[x]%m].modify(x,a[x]);
            printf("%lld\n",a[x]);
        }
        if(opt[]=='-')
        {
            if(a[x]<y) printf("%lld\n",a[x]);
            else
            {
                bit[a[x]%m].modify(x,-a[x]);
                a[x]-=y;
                bit[a[x]%m].modify(x,a[x]);
                printf("%lld\n",a[x]);
            }
        }
        if(opt[]=='s')
        {
            scanf("%d",&z);
            printf("%lld\n",bit[z].query(x,y));
        }
    }
    return ;
}