科学计算三维可视化---Mlab基础（基于Numpy数组的绘图函数）

Mlab了解

Mlab是Mayavi提供的面向脚本的api，他可以实现快速的三维可视化，Mayavi可以通过Mlab的绘图函数对Numpy数组建立可视化。

过程为：

.建立数据源

.使用Filter（可选）对数据进行加工

.添加可视化模块，我们可以通过修改可视化模块的属性，来修改可视化场景

mgrid和ogrid区别

一：基于Numpy数组的绘图函数

（一）3D绘图函数--Point3d（点图像0维）

这里我们可以看到Point3D参数的描述，是对vtk对象的整体描述，因为Mayavi是对VTK的整体封装，因此Mayavi建立的对象也就是VTK的对象

import numpy as np
from mayavi import mlab

#建立数据
t = np.linspace(,*np.pi,)   #linspace根据起止数据等间距填充数据，分为20组，所以下面将产生20个点
x = np.sin(*t)
y = np.cos(t)
z = np.cos(*t)
s =  + np.sin(t)

#对数据进行可视化
points = mlab.points3d(x,y,z,s,colormap="Reds",scale_factor=.)
mlab.show()

mlab.points3d(x,y,z,s,colormap="Reds",scale_factor=.) #x,y,z表示Numpy数组，列表或者其他形式的点三维坐标，s表示在该点处的标量值，scale_factor放缩比例

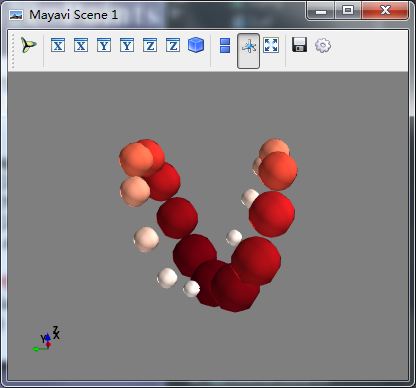
这里:标量值越大，点的尺寸越大，颜色越红

points = mlab.points3d(x,y,z,s,colormap="Greens",scale_factor=.)

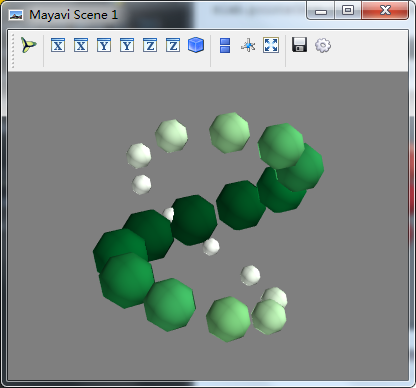
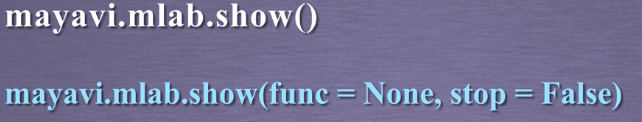
Mayavi.mlab.show建立了简单的GUI，并开始了事件循环，stop用来定义GUI的事件循环是否结束

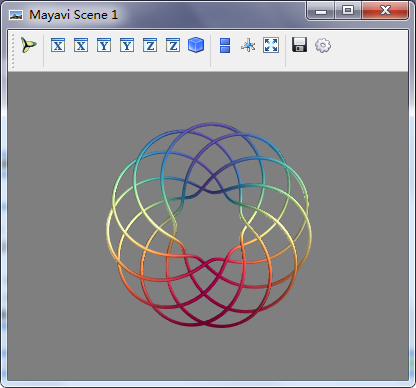
（二）3D绘图函数--plot3d（线图形一维）

import numpy as np
from mayavi import mlab　　#引入mlab库

#建立数据
n_mer,n_long = ,
dphi = np.pi / 1000.0
phi = np.arange(0.0,*np.pi+0.5*dphi,dphi)
mu = phi * n_mer
x = np.cos(mu)*(+np.cos(n_long*mu/n_mer)*0.5)
y = np.sin(mu)*(+np.cos(n_long*mu/n_mer)*0.5)
z = np.sin(n_long*mu/n_mer)*0.5

#对数据进行可视化
l = mlab.plot3d(x,y,z,np.sin(mu),tube_radius=0.025,colormap="Spectral")
mlab.show()

（三）3D绘图函数--2D数据（二维）

（1）imshow方法

import numpy as np
from mayavi import mlab

#建立数据
s = np.random.random((,))   #二维数据

#对数据进行可视化
img = mlab.imshow(s,colormap="gist_earth")  #gist_earth以地球表面的色彩为颜色的颜色映射关系
mlab.show()

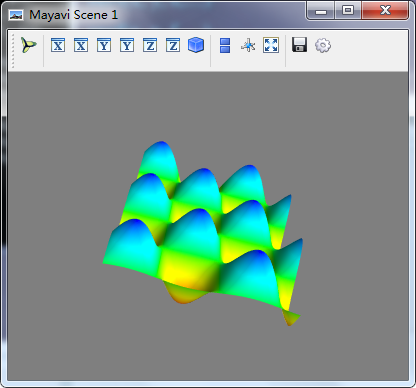
（2）surf方法

s:二维数组第一列表示x轴位置，第二列表示y轴位置，x,y可以是一维或者二维数组，一般情况下，他们都由numpy的mgrid或ogrid得到

import numpy as np
from mayavi import mlab

def f(x,y):
    return np.sin(x-y)+np.cos(x+y)

x,y = np.mgrid[-.:7.05:0.1,-.:5.05:0.05]
s = mlab.surf(x,y,f)
mlab.show()

mgrid返回两个二维数组（个数是不固定的，我们放置几个元素，就会生成几个二维数组）
-.:7.05:0.1---->最小-，最大7.，步长为0.1依次生成一个n*n矩阵

>>> x,y = np.mgrid[-.:7.05:0.1,-.:5.05:0.05]
>>> x
array([[-. , -. , -. , ..., -. , -. , -. ],
       [-6.9, -6.9, -6.9, ..., -6.9, -6.9, -6.9],
       [-6.8, -6.8, -6.8, ..., -6.8, -6.8, -6.8],
       ...,
       [ 6.8,  6.8,  6.8, ...,  6.8,  6.8,  6.8],
       [ 6.9,  6.9,  6.9, ...,  6.9,  6.9,  6.9],
       [ . ,  . ,  . , ...,  . ,  . ,  . ]])
>>> y
array([[-.  , -4.95, -4.9 , ...,  4.9 ,  4.95,  .  ],
       [-.  , -4.95, -4.9 , ...,  4.9 ,  4.95,  .  ],
       [-.  , -4.95, -4.9 , ...,  4.9 ,  4.95,  .  ],
       ...,
       [-.  , -4.95, -4.9 , ...,  4.9 ,  4.95,  .  ],
       [-.  , -4.95, -4.9 , ...,  4.9 ,  4.95,  .  ],
       [-.  , -4.95, -4.9 , ...,  4.9 ,  4.95,  .  ]])

（3）contour_surf() 与surf()类似，单求解的是等值线，surf求解的是曲面

import numpy as np
from mayavi import mlab

def f(x,y):
    return np.sin(x-y)+np.cos(x+y)

x,y = np.mgrid[-.:7.05:0.1,-.:5.05:0.05]
s = mlab.contour_surf(x,y,f)
mlab.show()

（四）3D绘图函数--3D数据（三维）

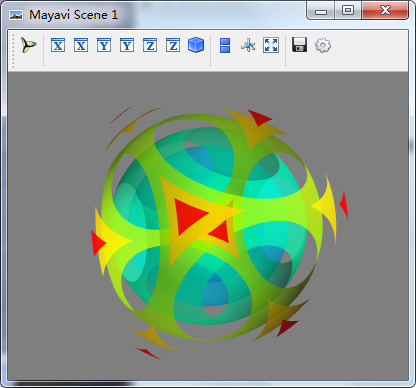
（1）contour3d方法

import numpy as np
from mayavi import mlab

x,y,z = np.ogrid[-::64j,-::64j,-::64j]　　#64j表示数组长度为64
scalars = x*x + y*y +z*z
obj = mlab.contour3d(scalars,contours=,transparent=True)　　#contours八个等值面　　transparent该对象可以透明表示，可以查看内部
mlab.show()

ogrid返回3个三维数组（几个是不固定的，我们设置了几个元素，就生成相对应个三维数组）

>>> x,y,z = np.ogrid[-::64j,-::64j,-::64j]
>>> x
array([[[-.        ]],　　#共64个元素

       [[-4.84126984]],

       [[-4.68253968]],

    　　.......
       [[ 4.68253968]],

       [[ 4.84126984]],

       [[ .        ]]])

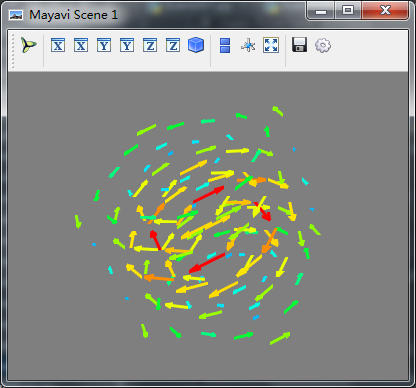
（2）quiver3d()方法

（x,y,z表示箭头位置，二维即可，不需要三维表示）

import numpy as np
from mayavi import mlab

x,y,z = np.mgrid[-2:3,-2:3,-2:3]
r = np.sqrt(x**2 + y**2 + z**4)
u = y*np.sin(r)/(r+0.001)
v = -x*np.sin(r)/(r+0.001)
w = np.zeros_like(z)

obj = mlab.quiver3d(x,y,z,u,v,w,line_width=3,scale_factor=1)
mlab.show()