ZOJ 3537 Cake（凸包+区间DP）

题目链接：http://acm.zju.edu.cn/onlinejudge/showProblem.do?problemCode=3537

题目大意：给出一些点表示多边形顶点的位置，如果不是凸多边形（凸包）则不能切，直接输出"I can't cut."
切多边形时每次只能在顶点和顶点间切，每切一次的花费为 cost(i, j) = |xi + xj| * |yi + yj| % p。
问把多边形切成最多个不相交三角形的最小代价是多少。

解题思路：先求出凸包，接着可以用区间DP解决，设dp[i][j]为以i为起点，j为终点的凸包被切成三角形的最小花费。
那么可以得到状态转移方程：dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j]+cost[i][k]+cost[k][j])。
不懂的可以看下图（非原创）：

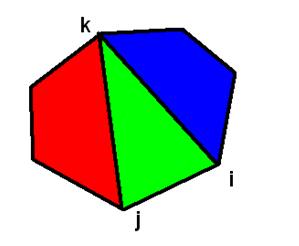
代码：

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<vector>
 #include<cmath>
 #include<algorithm>
 using namespace std;
 const int INF=0x3f3f3f3f;
 const int N=;
 const double eps = 1e-;
 
 int n,mod;
 int dp[N][N],cost[N][N];
 
 struct P
 {
     double x, y;
     P(double x=, double y=):x(x), y(y) {}
     double add(double a, double b){
         if(fabs(a+b)<eps*(fabs(a)+fabs(b))) return ;
         return a+b;
     }
     P operator + (P p){
         return P(add(x, p.x), add(y, p.y));
     }
     P operator - (P p){
         return P(add(x, -p.x), add(y, -p.y));
     }
     P operator *(double d){
         return P(x*d, y*d);
     }
     double dot(P p){                 //点积
         return add(x*p.x, y*p.y);
     }
     double det(P p){                 //差积
         return add(x*p.y, -y*p.x);
     }
 }ps[N];
 
 double dist(P a, P b){
     return sqrt((b-a).dot(b-a));
 }
 
 bool cmp_x(const P& p, const P& q){
     if(p.x!=q.x) return p.x < q.x;
     return p.y < q.y;
 }
 
 vector<P> convex_hull(P *ps, int n){
     sort(ps,ps+n,cmp_x);
     int k = ;          //凸包顶点数
     vector<P> qs(n*);
     //构造凸包的下侧
     for(int i=; i<n; i++)
     {
         while(k> && (qs[k-]-qs[k-]).det(ps[i]-qs[k-])<=) k--;
         qs[k++] = ps[i];
     }
     //构造凸包的上侧
     for(int i=n-,t=k; i>=; i--)
     {
         while(k>t && (qs[k-]-qs[k-]).det(ps[i]-qs[k-])<=) k--;
         qs[k++] = ps[i];
     }
     qs.resize(k-);
     return qs;
 }
 
 int getcost(P p1,P p2){
     return abs((int)p1.x+(int)p2.x)*abs((int)p1.y+(int)p2.y)%mod;
 }
 
 int main(){
     while(~scanf("%d%d",&n,&mod)){
         for(int i=;i<n;i++){
             scanf("%lf%lf",&ps[i].x,&ps[i].y);
         }
         vector<P>tp;
         tp=convex_hull(ps,n);
         if(tp.size()<n){
             puts("I can't cut.");
             continue;
         }
         //注意，用获得的凸包做DP，即使用tp做DP,保证凸包上的点的顺序
         memset(cost,,sizeof(cost));
         memset(dp,,sizeof(dp));
         for(int i=;i<n;i++){
             for(int j=i+;j<n;j++){
                 cost[i][j]=getcost(tp[i],tp[j]);
             }
         }
         for(int len=;len<n;len++){
             for(int i=;i+len<n;i++){
                 int j=i+len;
                 dp[i][j]=INF;
                 for(int k=i+;k<=j-;k++){
                     dp[i][j]=min(dp[i][j],dp[i][k]+dp[k][j]+cost[i][k]+cost[k][j]);
                 }
             }
         }
         printf("%d\n",dp[][n-]);
     }
     return ;
 }