css四种选择器总结

css 在网页开发中扮演着重要的角色，被誉为网页开发的三剑客,如果说html是人的外在器官部分，那css无疑是各个器官组成在一起然后表现出来，css又称样式重叠在网页排版布局中的地位举足轻重。

  做为后端开发者来说，学好css样式也是快速入门各类框架的基础，也是做为一名全栈工程师必备的知 识,下面来说说css中重要的选择器，

      在css中常见的选择器有四种常见,说到选择器就不得不说css引入文件的常见的三种方法，1，内联文件，2，外部文件，3.内嵌文件 ，其中三种常规的例子如下

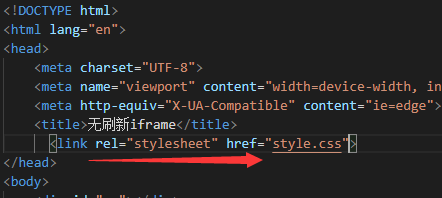
1，借助link标签来引入“外部文件“，href 则代表其路径文件属性

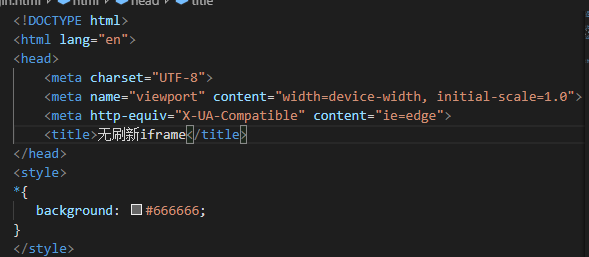
2,中则是"内嵌文件" 在html /head 标签下面 style之内

3.内联在html代码中被称为"内联文件"。

   之所以讲三种引入样式文件方法，是因为他们与选择器息息相关，

  总结：1，不管哪一种方式，都得先找到 对应元素，对应id，对应class，或是全局通配，才能赋予其css样式。

             2，三种方式存在着优先级，内联>内嵌>外部。

             3,目前较为流行的是外部样式。

1,在html代码中标有 id=“***“时就是 id 选择器，在css样式中则用#号获取该id

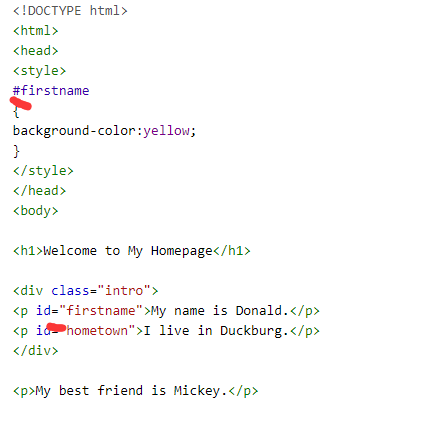
      ps； 以#号做开始标志选中赋予其背景颜色黄色 说明#id具有唯一性，

1,在html代码中标有 class=“***“时就是 class 选择器，在css样式中则用.号获取该id

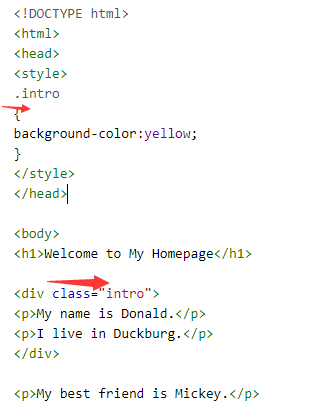
 3,元素选择器中 没有class ，id 只有标签的称为元素 h1-6标签  p 或 div span等 就是个元素

ps:元素之间可以相互找下级元素以逗分割；如下

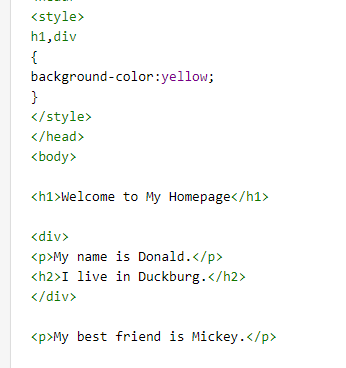
这个样式包含h1与div元素 都会被显示黄色背景，h1与div之外的不会显示

4,通配*用来做全局的适配常用来初始化：如下：

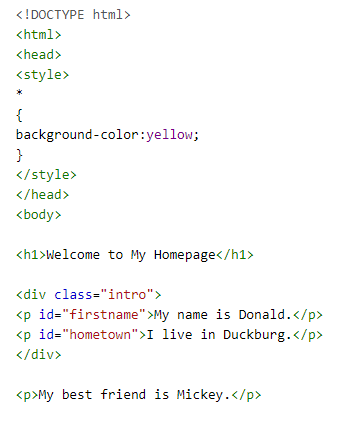
ps：全部设置背景颜色黄色

总结；在网页排版中可以灵活运用以上四种常见的选择器，繁衍出高级的选择器。