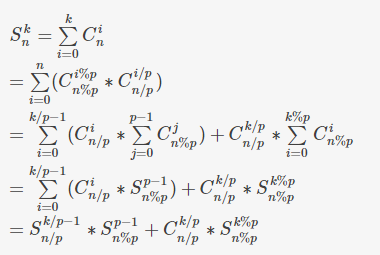[BZOJ 4591] 超能粒子炮-改
Link:
Solution:
记录一下推$\sum_{i=0}^k C_n^i$的过程:
其实就是将相同的$i/p$合起来算,这样每个里面都是一个可以预处理的子问题
接下来递归下去算即可
Tip:推式子时尽量化出与模数相关的量方便预处理
Code:
#include <bits/stdc++.h> using namespace std;
#define X first
#define Y second
#define pb push_back
typedef double db;
typedef long long ll;
typedef pair<int,int> P;
int T;const int MOD=;
ll C[MOD+][MOD+],sum[MOD+][MOD+]; ll Lucas(ll x,ll y)
{
if(y==) return ;
return Lucas(x/MOD,y/MOD)*C[x%MOD][y%MOD]%MOD;
}
ll cal(ll n,ll k)
{
if (k<) return ;
return (cal(n/MOD,k/MOD-)*sum[n%MOD][MOD-]+Lucas(n/MOD,k/MOD)*sum[n%MOD][k%MOD])%MOD;
}
int main()
{
C[][]=;sum[][]=;
for (int i=;i<MOD;i++) sum[][i]=;
for (int i=;i<MOD;i++)
{
C[i][]=sum[i][]=;
for (int j=;j<=i;j++) C[i][j]=(C[i-][j-]+C[i-][j])%MOD;
for (int j=;j<MOD;j++) sum[i][j]=(sum[i][j-]+C[i][j])%MOD;
}
scanf("%d",&T);
while (T--)
{
ll n,k;
scanf("%lld%lld",&n,&k);
printf("%lld\n",cal(n,k));
}
return ;
}
[BZOJ 4591] 超能粒子炮-改的更多相关文章
- bzoj 4591 超能粒子炮·改 - Lucas
Description 曾经发明了脑洞治疗仪&超能粒子炮的发明家SHTSC又公开了他的新发明:超能粒子炮·改--一种可以发射威力更加 强大的粒子流的神秘装置.超能粒子炮·改相比超能粒子炮,在威 ...
- Bzoj 4591: [Shoi2015]超能粒子炮·改 数论,Lucas定理,排列组合
4591: [Shoi2015]超能粒子炮·改 Time Limit: 10 Sec Memory Limit: 256 MBSubmit: 178 Solved: 70[Submit][Stat ...
- bzoj 4591: [Shoi2015]超能粒子炮·改 [lucas定理]
4591: [Shoi2015]超能粒子炮·改 题意:多组询问,求 \[ S(n, k) = \sum_{i=0}^n \binom{n}{i} \mod 2333,\ k \le n \le 10^ ...
- BZOJ 4591 【SHOI2015】 超能粒子炮·改
题目链接:超能粒子炮·改 这道题的大体思路就是用\(lucas\)定理,然后合并同类项,就可以得到一个可以递归算的式子了. 我们用\(S(n,k)\)表示答案,\(p\)表示模数(\(2333\)是一 ...
- 【BZOJ-4591】超能粒子炮·改 数论 + 组合数 + Lucas定理
4591: [Shoi2015]超能粒子炮·改 Time Limit: 10 Sec Memory Limit: 256 MBSubmit: 95 Solved: 33[Submit][Statu ...
- 【BZOJ4591】[SHOI2015]超能粒子炮·改 (卢卡斯定理)
[BZOJ4591][SHOI2015]超能粒子炮·改 (卢卡斯定理) 题面 BZOJ 洛谷 题解 感天动地!终于不是拓展卢卡斯了!我看到了一个模数,它是质数!!! 看着这个东西就感觉可以递归处理. ...
- 洛谷 P4345 [SHOI2015]超能粒子炮·改 解题报告
P4345 [SHOI2015]超能粒子炮·改 题意 求\(\sum_{i=0}^k\binom{n}{i}\),\(T\)组数据 范围 \(T\le 10^5,n,j\le 10^{18}\) 设\ ...
- loj#2038. 「SHOI2015」超能粒子炮・改
题目链接 loj#2038. 「SHOI2015」超能粒子炮・改 题解 卢卡斯定理 之后对于%p分类 剩下的是个子问题递归 n,k小于p的S可以预处理,C可以卢卡斯算 代码 #include<c ...
- bzoj4591 / P4345 [SHOI2015]超能粒子炮·改
P4345 [SHOI2015]超能粒子炮·改 题意:求$\sum_{i=1}^{k}C(n,i)\%(P=2333)$ 肯定要先拆开,不然怎么做呢(大雾) 把$C(n,i)$用$lucas$分解一下 ...
随机推荐
- 两个Bounding Box的IOU计算代码
Bounding Box的数据结构为(xmin,ymin,xmax,ymax) 输入:box1,box2 输出:IOU值 import numpy as np def iou(box1,box2): ...
- 十一、springboot之web开发之Filter
我们常常在项目中会使用filters用于录调用日志.排除有XSS威胁的字符.执行权限验证等等.Spring Boot自动添加了OrderedCharacterEncodingFilter和Hidden ...
- OSGiBundle出现 Could not find bundle: org.eclipse.equinox.console的解决方案
按照网上教程创建OSGI HelloWorld实例配置run configuration时出现Could not find bundle: org.eclipse.equinox.console 和C ...
- Flask:使用jsonify()转换为JSON的数据在Chrome显示为Unicode编码
Chrome 66,Flask 1.0.2,MongoDB 3.6.3, 创建了一个Flask应用,在将MongoDB中的数据使用PyMongo包获取后,再使用jsonify转换为JSON格式发送回请 ...
- php rabbitmq的扩展
1.下载:https://github.com/alanxz/rabbitmq-c/archive/v0.9.0.tar.gz mkdir build && cd build # 这一 ...
- 使用Appium 测试微信小程序和微信公众号方法
由于腾讯系QQ.微信等都是基于腾讯自研X5内核,不是google原生webview,需要打开TBS内核Inspector调试功能才能用Chrome浏览器查看页面元素,并实现Appium自动化测试微信小 ...
- master..xp_fileexist
declare @sql varchar(800) set @sql='E:\temp.dbf'create table #tb(a bit,b bit,c bit) insert into #t ...
- MySQL 存储过程入门
存储过程是带有逻辑的SQL语句,优点是执行效率高.缺点是可移植性差 1.存储过程语法 DELIMITER $ --声明结束符 CREATE PROCEDURE pro_test() --创建存储过程 ...
- Django数据库数据表操作
建立表单 django通过设置类来快速建表,打开models.py 例: from __future__ import unicode_literals from django.db import m ...
- Asp.net MVC NPOI导出Excel
public class NpoiMemoryStream : MemoryStream { public NpoiMemoryStream() { AllowClose = true; } publ ...