【POJ】1419：Graph Coloring【普通图最大点独立集】【最大团】

Graph Coloring

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 5775		Accepted: 2678		Special Judge

Description

You are to write a program that tries to find an optimal coloring for a given graph. Colors are applied to the nodes of the graph and the only available colors are black and white. The coloring of the graph is called optimal if a maximum of nodes is black. The coloring is restricted by the rule that no two connected nodes may be black.

 
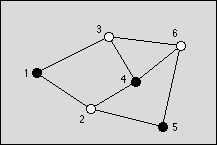
Figure 1: An optimal graph with three black nodes 

Input

The graph is given as a set of nodes denoted by numbers 1...n, n <= 100, and a set of undirected edges denoted by pairs of node numbers (n1, n2), n1 != n2. The input file contains m graphs. The number m is given on the first line. The first line of each graph contains n and k, the number of nodes and the number of edges, respectively. The following k lines contain the edges given by a pair of node numbers, which are separated by a space.

Output

The output should consists of 2m lines, two lines for each graph found in the input file. The first line of should contain the maximum number of nodes that can be colored black in the graph. The second line should contain one possible optimal coloring. It is given by the list of black nodes, separated by a blank.

Sample Input

1
6 8
1 2
1 3
2 4
2 5
3 4
3 6
4 6
5 6

Sample Output

3
1 4 5

---

Solution

最大点独立集？？？

差点就拍二分图叻....

然后发现这道题根本没法二分图啊？？就是个普通图？

上网学习才发现，二分图最大点独立集=顶点数-最大匹配，普通图最大点独立集=补图的最大团

然而补图是啥...最大团是啥....

图G的补图，通俗的来讲就是完全图Kn去除G的边集后得到的图Kn-G。在图论里面，一个图G的补图（complement）或者反面（inverse）是一个图有着跟G相同的点，而且这些点之间有边相连当且仅当在G里面他们没有边相连。

如果U V，且对任意两个顶点u，v∈U有(u,v)∈E，则称U是G的完全子图。G的完全子图U是G的团。G的最大团是指G的最大完全子图。

显然，原图的最大点独立集在补图中肯定两两相邻，所以求补图的最大团就是原图的最大点独立集。

用dfs求解，需要剪枝！

Code

#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;

int n, m, maxn, num;
int use[], now[], G[][];
void dfs(int x) {
    if(x > n) {
        maxn = num;
        for(int i = ; i <= n; i ++)
            use[i] = now[i];
        return ;
    }
    int flag = ;
    for(int i = ; i < x; i ++) {
        if(now[i] && !G[i][x]) {//////如果之前选了的点与现在的点没有相邻 现在这个点就不能在当前团里面
            flag = ;    break;
        }
    }
    if(flag) {
        num ++;
        now[x] = ;
        dfs(x + );
        num --;
        now[x] = ;
    }
    if(num + n - x > maxn)    dfs(x + );
}

int main() {
    int T;
    scanf("%d", &T);
    while(T --) {
        memset(G, , sizeof(G));
        memset(now, , sizeof(now));
        memset(use, , sizeof(use));
        scanf("%d%d", &n, &m);
        for(int i = ; i <= m; i ++) {
            int u, v;
            scanf("%d%d", &u, &v);
            G[u][v] = G[v][u] = ; ////////补图
        }
        num = maxn = ;
        dfs();
        printf("%d\n", maxn);
        for(int i = ; i <= n; i ++)
            if(use[i])    printf("%d ", i);
        printf("\n");
    }
    return ;
}