2668: [cqoi2012]交换棋子

Description

有一个n行m列的黑白棋盘，你每次可以交换两个相邻格子（相邻是指有公共边或公共顶点）中的棋子，最终达到目标状态。要求第i行第j列的格子只能参与mi,j次交换。

Input

第一行包含两个整数n，m（1<=n, m<=20）。以下n行为初始状态，每行为一个包含m个字符的01串，其中0表示黑色棋子，1表示白色棋子。以下n行为目标状态，格式同初始状态。以下n行每行为一个包含m个0~9数字的字符串，表示每个格子参与交换的次数上限。

Output

输出仅一行，为最小交换总次数。如果无解，输出-1。

---

写了一个很假的做法

但是居然正解也是这样的？？

好吧好吧

那这题也太丧病了

---

先想一下这道题的基本建模思路，就是把它想象成一些黑点在一张图上流动，如果一个点初始时是黑色就从源点流一个流量一的边，如果遇到一个目标是黑色的点就可以流去汇点

初始版本 1.0 (甚至能得60分)

然后考虑拆两个点

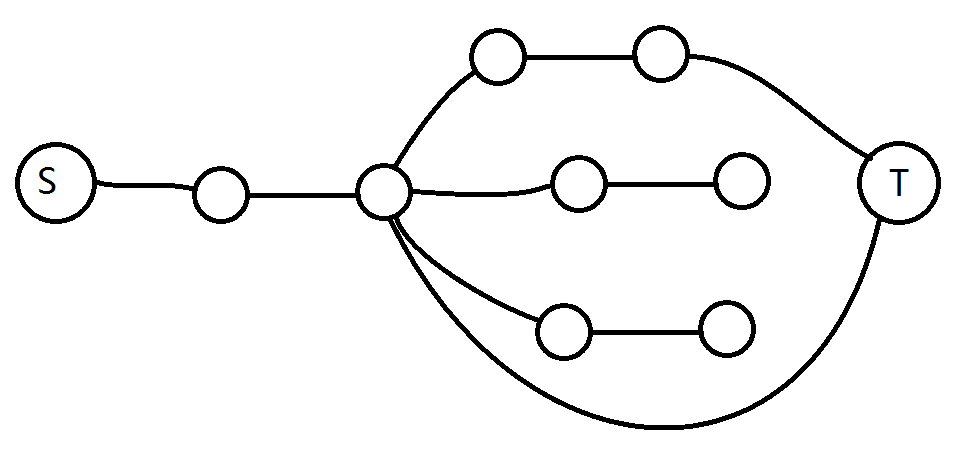
没前途啊

考虑到一个位置上换来一个点然后再换走的话这个位置被换了2次

但是这个模型没法处理啊。。。

优化版本 1.5

拆成3个点！

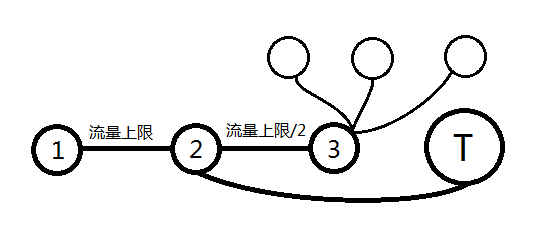
怎么说呢。。。比1.0还没前途啊

因为如果这个点本来是黑色的但是它的流量是1

那么它就流不过去了。。。

正解 2.0

如果这个点就是黑色的就把2到3的流量改成（流量上限+1）/2不就完了

然后就喜提满分了？？

---

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
#define MP make_pair
#define TS top().second
#define M 1000001
#define N 50000
//#define gc getchar
using namespace std;

priority_queue<pair<int,int> >q;
int uu,a[M],t,n,m,k,ver[M],edge[M],head[N],nex[M],cnt=1,d[N],h[N],c[M],g[N],x,y,z,s,b[N],cur[N],ans,cost,w[M];
void add(int x,int y,int co,int z)
{
	ver[++cnt]=y; nex[cnt]=head[x]; head[x]=cnt; edge[cnt]=z; c[cnt]=co;
	ver[++cnt]=x; nex[cnt]=head[y]; head[y]=cnt; edge[cnt]=0; c[cnt]=-co;
}

bool dji()
{
	while(q.size()) q.pop();
	memset(d,0,sizeof(d)); memset(g,0x3f,sizeof(g)); memset(b,0,sizeof(b));
	d[0]=1; g[0]=0; q.push(MP(0,0));
	while(q.size())
	{
		while(q.size() && b[q.TS]) q.pop();
		if(!q.size()) break;
		int x=q.TS; q.pop(); b[x]=1;
		for(int i=head[x];i;i=nex[i])
		if(edge[i] && g[ver[i]]>g[x]+c[i]+h[x]-h[ver[i]])
		{
			g[ver[i]]=g[x]+c[i]+h[x]-h[ver[i]];
			d[ver[i]]=d[x]+1;
			q.push(MP(-g[ver[i]],ver[i]));
		}
	}
	if(g[t]<0x3f3f3f3f) return 1;
	return 0;
}

int dinic(int x,int flow)
{
	if(x==t || !flow) return flow;
	int re=flow, k;
	for(int& i=cur[x];i && re;i=nex[i])
	if(edge[i] && d[ver[i]]==d[x]+1 && g[ver[i]]==g[x]+c[i]+h[x]-h[ver[i]])
	{
		k=dinic(ver[i],min(re,edge[i]));
		re-=k; edge[i]-=k; edge[i^1]+=k;
		if(!k) d[ver[i]]=0;
	}
	return flow-re;
}

int main()
{
	scanf("%d%d",&n,&m); t=n*m*3+1;
	for(int i=0;i<n;i++)
		for(int j=1;j<=m;j++)
		{
			scanf("%1ld",&k);
			if(k) a[i*m+j]=1, uu+=1;
		}
	for(int i=0;i<n;i++)
		for(int j=1;j<=m;j++)
		{
			scanf("%1ld",&k);
			if(k) w[i*m+j]=1, uu-=1;
			if(i) add(i*m+j+n*m*2,(i-1)*m+j,1,0x3f3f3f3f);
			if(j!=1) add(i*m+j+n*m*2,i*m+j-1,1,0x3f3f3f3f);
			if(i && j!=1) add(i*m+j+n*m*2,(i-1)*m+j-1,1,0x3f3f3f3f);
			if(i && j!=m) add(i*m+j+n*m*2,(i-1)*m+j+1,1,0x3f3f3f3f);
			if(j!=m) add(i*m+j+n*m*2,i*m+j+1,1,0x3f3f3f3f);
			if(i!=n-1) add(i*m+j+n*m*2,(i+1)*m+j,1,0x3f3f3f3f);
			if(j!=m && i!=n-1) add(i*m+j+n*m*2,(i+1)*m+j+1,1,0x3f3f3f3f);
			if(j!=1 && i!=n-1) add(i*m+j+n*m*2,(i+1)*m+j-1,1,0x3f3f3f3f);
		}
	if(uu!=0){printf("-1"); return 0;}
	for(int i=1;i<=n*m;i++)
	{
		if(w[i]) add(i+n*m,t,0,1);
		if(a[i]) add(0,i,0,1);
	}
	for(int i=0;i<n;i++)
		for(int j=1;j<=m;j++)
		{
			scanf("%1ld",&k);
			if(k)add(i*m+j,i*m+j+n*m,0,k);
			if(k && (w[i*m+j]||a[i*m+j])) add(i*m+j+n*m,i*m+j+n*m*2,0,(k+1)/2);
			else add(i*m+j+n*m,i*m+j+n*m*2,0,k/2);
		}

	while(dji())
	{
		memcpy(cur,head,sizeof(head)); z=ans;
		while(k=dinic(0,0x3f3f3f3f)) ans+=k;
		for(int i=1;i<=t;i++) h[i]+=g[i];
		cost+=(ans-z)*h[t];
	}
	printf("%d",cost);
}