PSO算法的改进（参数）

## 基本PSO的改进

虽然粒子群在求解优化函数时，表现了较好的寻优能力；通过迭代寻优计算，能够迅速找到近似解；
但基本的PSO容易陷入局部最优，导致结果误差较大。

两个方面：
1.将各种先进理论引入到PSO算法，研究各种改进和PSO算法；（混沌技术，神经网络技术，自适应技术）
2.将PSO算法和其它智能优化算法相结合，研究各种混合优化算法，
达到取长补短、改善算法某方面性能的效果。

近时期粒子群改进策略主要体现的方面：
1.PSO算法的惯性权重模型，通过惯性权重的引入，提高了算法的全局搜索能力；
2.带邻域操作的PSO模型，克服PSO模型在优化搜索后期随迭代次数增加搜索结果无明显改进的缺点；
3.协同PSO算法，用K个相互独立的粒子群分别在D维的目标搜索空问中的不同维度方向上进行搜索；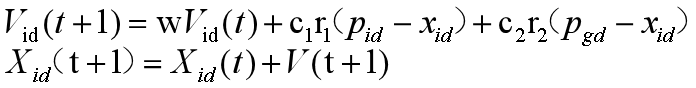

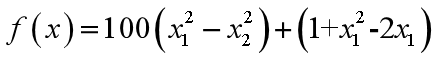
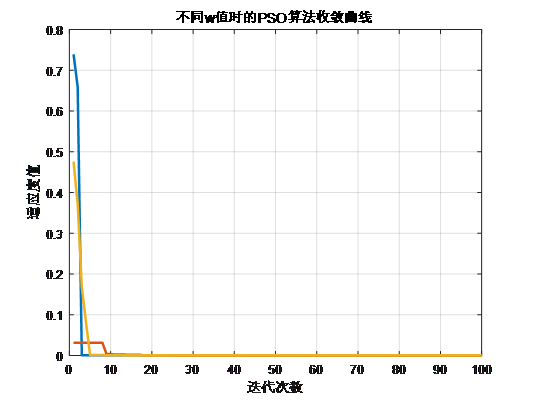
*蓝色的曲线：w=0.8，黄色的曲线：w=0.6红色的曲线：w=0.4*

从上式可以看出，w越大，微粒飞行速度越大，微粒将以较大的步长进行全局搜索；w越小，则微粒步长小，趋向于精细的局部搜索。

同时，从右图也可以看出w=0.8时，微粒以更少的迭代次数取得全局最优；w=0.6时，迭代次数其次，
w=0.4时，迭代次数相对较多。

虽然较大的权重因子有利于跳出局部最小值，便于全局搜索，而较小的惯性因子则有利于对当前的搜索区域进行精确局部搜索，以利于算法收敛；但是w过大容易导致“早熟收敛”与算法后期在全局最优解附近产生振荡的现象。

**w的改进**

一般方法是把Wmax逐渐变成Wmin；

**1.权重线性递减的PSO算法**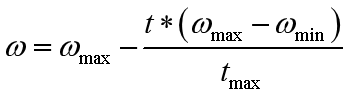

  

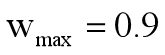
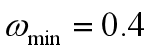
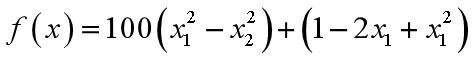
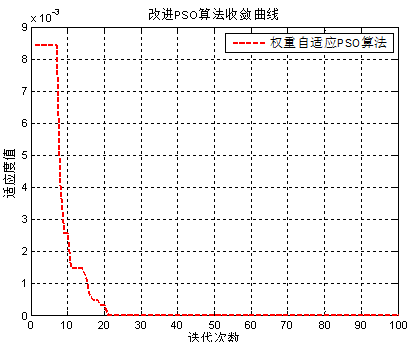
                     自适应权重粒子群优化算法适应度曲线

2.自适应权重的PSO算法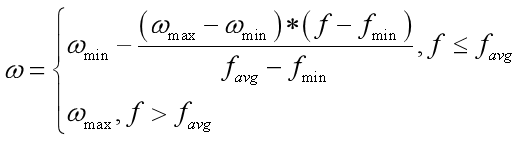

f表示微粒当前的目标函数值。
当各微粒的目标值趋于一致或趋于局部最优时，将使惯性权重增大，而各微粒的目标值比较分散时，使惯性权重减小，同时对于目标函数值优于平均目标值的微粒，其对应的惯性权重因子较小，从而保留了该微粒，反之对于目标函数值差于平均目标值的微粒，其对应的惯性权重因子较大，使得该微粒向较好的搜索区域靠拢。（附图）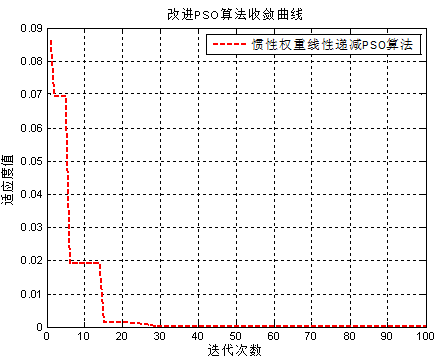

                           惯性权重线性递减PSO算法适应度曲线

3.随机权重策略的PSO算法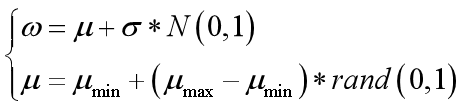

随机地选取值，使得微粒历史速度对当前速度的影响是随机的。
为服从某种随机分布的随机数，从一定程度上可从两方面克服 w的线性递减所带来的不足。
随机权重策略的PSO算法对于多峰函数，能在一定程度上避免陷入局部最优。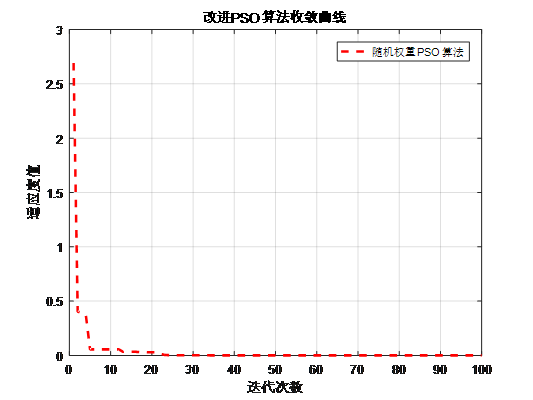

[随机权重策略的PSO适应度曲线]

4.增加收缩因子的PSO算法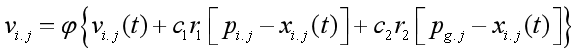

          

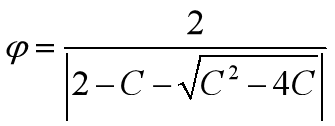
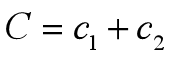
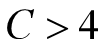
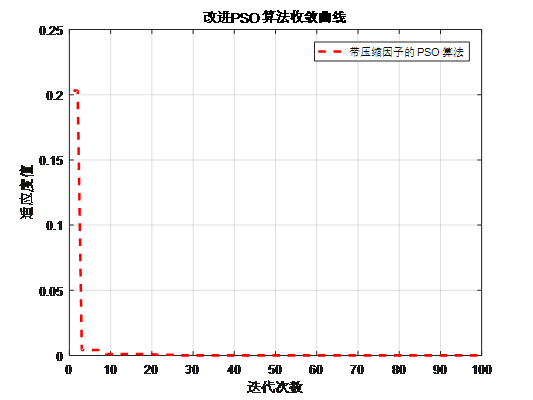
压缩因子 比惯性权重系数w更能有效地控制与约束微粒的飞行速度，同时也增强了算法的局部搜索能力。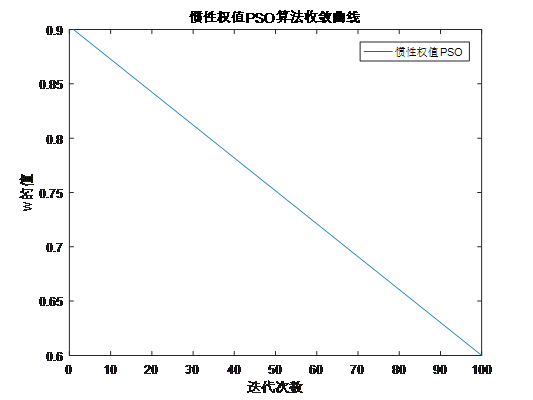

带压缩因子的的PSO算法适应度曲线

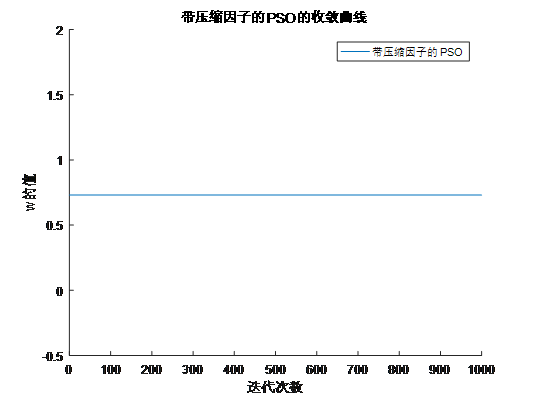
由上面两个图，可以看出惯性常数方法通常采用惯性权值随更新代数增加而递减的策略，在算法后期由于惯性权值过小，会失去微粒的探索新区域的能力，而压缩因子方法则不存在此不足。

**CONCLUTIONS**
PSO算法的搜索性能取决于其全局搜索与局部改良能力的平衡，这很大程度上依赖于算法的参数控制，包括N，Vmax，M，w，c1,c2等;

**微粒种群数目N**：N设置较小时，算法收敛速度快，但是容易陷入局部最优；N设置较大时，算法收敛速度相对较慢；导致计算时间大幅增加，而且群体数目N增至一定的水平时，再增加微粒数目不再有显著的效果。

参考取值：一般设N为10~50之间，对于比较复杂的问题，微粒数目N可以取100以上；

**最大速度Vmax**：决定搜索的力度；Vmax过大，粒子运动速度快，微粒探索能力强，但容易越过最优的搜索空间，错过最优解；如果Vmax较小，微粒的开发能力强，容易进入局部最优，可能会使微粒无法运动足够远的距离以跳出局部最优，从而也可能找不到解空间的最佳位置。（跟w的取值规则一样）。

**惯性权值w**：w越大，微粒飞行速度越大，微粒将会以更长的步长进行全局搜索；w较小，则微粒步长小，趋向于精细的局部搜索；因此，我们采用动态改变w的值；在搜索初期设w取一个较大值，然后随着迭代次数的不断增加，逐渐降低w的值；从而达到全局最优。

**ways**：随机调整,线性递减，非线性递减，模糊自适应。

**学习因子c1，c2**：c1,c2具有自我总结和向优秀个体学习的能力，从而使微粒向群体内或领域内的最优点靠近。c1，c2分别调节微粒向个体最优或者群体最优方向飞行的最大步长，决定微粒个体经验和群体经验对微粒自身运行轨迹的影响。学习因子较小时，可能使微粒在远离目标区域内徘徊；学习因子较大时，可使微粒迅速向目标区域移动，甚至超过目标区域。因此，c1和c2的搭配不同，将会影响到PSO算法的性能。

**ways**：一般令c1+c2=4；其实c1=2附近的迭代次数较小，在两个端点0和4附近的迭代次数较大，大致呈现出对称性；在俩端点处搜索失败率较大；通常，越接近端点，失败率越高。但并不是所有情况都是c1=c2=2时才有最优解。

r1，r2是[0,1]之间的随机数。

**最大迭代次数M**：算法停止迭代条件。

另外，随着变量范围和维数的增加，搜索空间呈几何级扩张，迭代次数相应增加，优化函数越复杂，所需的计算量越大，迭代次数也越多。

参数的选择影响算法的性能和效率，也是一个值得优化的问题。在实际应用中，没有选择参数的通用方法，只能凭经验选取。大量的仿真实验发现，参数对算法性能的影响有一定的规律可寻。例如：w=0.7298，c1=c2=1.49618是一组较为出色的参数组合。
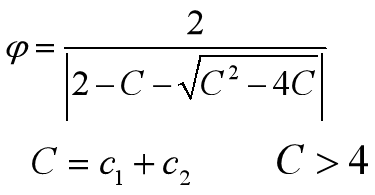
谢谢大家~~~~~~
欢迎大家和我一起讨论，一起进步。
有需求可联系本人邮箱qinwei1005@foxmail.com