Luogu 1220 关路灯（动态规划）

Description

某一村庄在一条路线上安装了n盏路灯，每盏灯的功率有大有小（即同一段时间内消耗的电量有多有少）。老张就住在这条路中间某一路灯旁，他有一项工作就是每天早上天亮时一盏一盏地关掉这些路灯。

为了给村里节省电费，老张记录下了每盏路灯的位置和功率，他每次关灯时也都是尽快地去关，但是老张不知道怎样去关灯才能够最节省电。他每天都是在天亮时首先关掉自己所处位置的路灯，然后可以向左也可以向右去关灯。开始他以为先算一下左边路灯的总功率再算一下右边路灯的总功率，然后选择先关掉功率大的一边，再回过头来关掉另一边的路灯，而事实并非如此，因为在关的过程中适当地调头有可能会更省一些。

现在已知老张走的速度为1m/s，每个路灯的位置（是一个整数，即距路线起点的距离，单位：m）、功率（W），老张关灯所用的时间很短而可以忽略不计。

请你为老张编一程序来安排关灯的顺序，使从老张开始关灯时刻算起所有灯消耗电最少（灯关掉后便不再消耗电了）。

Input

文件第一行是两个数字n(0<n<50，表示路灯的总数)和c(1<＝c<=n老张所处位置的路灯号)；

接下来n行，每行两个数据，表示第1盏到第n盏路灯的位置和功率。

Output

一个数据，即最少的功耗(单位：J，1J＝1W·s)。

Sample Input

5 3

2 10

3 20

5 20

6 30

8 10

Sample Output

270

Http

Luogu:https://www.luogu.org/problem/show?pid=1220

Source

动态规划

解决思路

这个题目首先要想明白一点，就是如果从i走到j，那么i到j之间的等都是关掉了的。另外，如果关闭了i到j之间的灯，那么现在一定停在i处或j处。

因为如果不是这样的话就会浪费时间，而题目要求求最优解。

想明白了上面的两条后，推导出状态转移方程就相对好办啦。

我们设F[i][j]表示关闭i到j这一区间内的所有灯所消耗的最小功率，那么为了表示最后是停在那边，我们再加一维,F[i][j][0]表示最后停在左边i处，F[i][j][1]表示最后停在右边j处。

接下来我们来看一看如何推导出状态转移方程。

对于F[i][j]，我们发现它可以从F[i+1][j]和F[i][j-1]推导过来，我们分别来看：

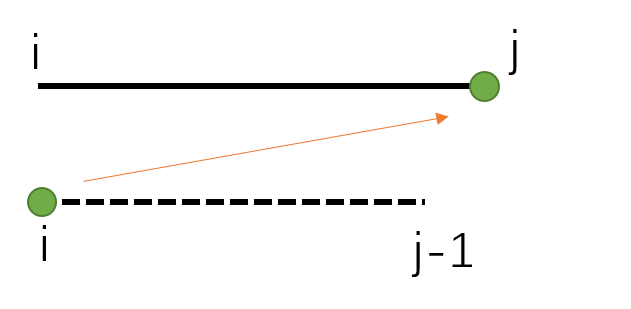
首先来看从F[i+1][j]推过来的情况

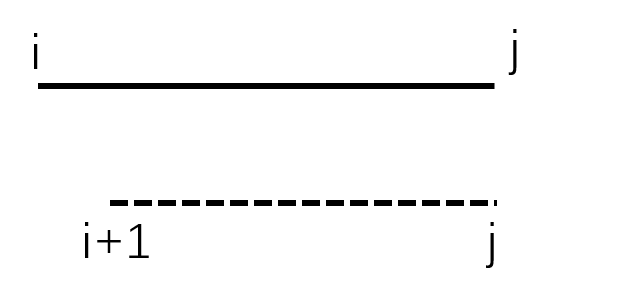
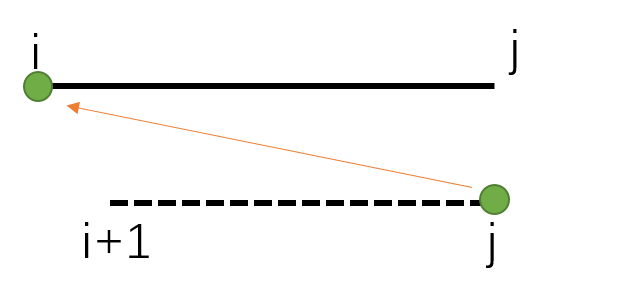
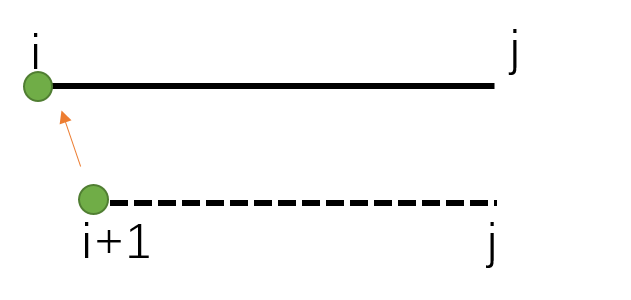
我们发现，老张可以从j走到i，也可以从i+1走到i，但不能从i+1走到j（因为这样并不能关掉i号灯），也不能从j走到（这样没有意义）。所以综上我们能从F[i+1][j][3]和F[i+1][j][2]推出F[i][j][0]

也就是这么走：

或者是这么走：

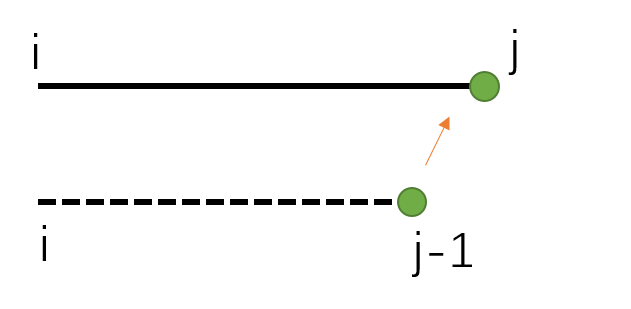
再来看看从F[i][j-1]推过来的情况

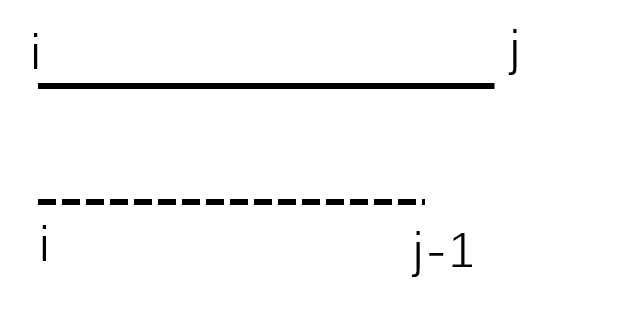
我们发现可以从i走到j，也可以从j-1走到j，所以我们可以从F[i][j-1][0]和F[i][j-1][1]推出F[i][j][1]

用图表示就是：

和

最后总结一下，状态转移方程就是：

\[F[i][j][0]=min\begin{cases} F[i+1][j][0]+(D[i+1]-D[i])*(Sum[n]-Sum[j]+Sum[i]) \\ F[i+1][j][1]+(D[j]-D[i])*(Sum[n]-Sum[j]+Sum[i])) \end{cases}
\]

\[F[i][j][1]=min\begin{cases}F[i][j-1][0]+(D[j]-D[i])*(Sum[n]-Sum[j-1]+Sum[i-1]) \\F[i][j-1][1]+(D[j]-D[j-1])*(Sum[n]-Sum[j-1]+Sum[i-1])) \end{cases}
\]

解释一下，Sum是为了方便处理剩余未关电灯的功率数而提前计算的前缀和，Sum[i]表示从1到i的所有电灯的功率之和，那么因为我们关掉的是i到j-1或i+1到j，所以我们只要通过前缀和计算减去这一部分就可以，但要注意i和j号灯是否被关闭，因为我们推导F[i][j][0]和F[i][j][1]时的转移方程不太一样，细节要注意。

另外就是要注意，循环时的循环初值和终值，虽然说F[i][j]必须包括老张出发时在的那盏灯，但为了动归转移时不会出现漏项，所以要处理一下，具体请看代码。

代码

#include<iostream>

#include<cstdio>

#include<cstdlib>

#include<cstring>

#include<algorithm>

using namespace std;

const int maxN=60;

const int inf=147483647;

int n,C;

int F[maxN][maxN][3];

int Sum[maxN];

int D[maxN];

int P[maxN];

int main()

{

    cin>>n>>C;

    Sum[0]=0;//注意前缀和初始化

    for (int i=0;i<=n;i++)

        for (int j=0;j<=n;j++)

            F[i][j][0]=F[i][j][1]=inf;//因为F要取最小，所以先置无穷大初值。

    for (int i=1;i<=n;i++)

    {

        cin>>D[i]>>P[i];

        Sum[i]=Sum[i-1]+P[i];//输入的同时计算前缀和

    }

    F[C][C][1]=F[C][C][0]=0;//初值

    for (int i=C;i>=1;i--)

        for (int j=i+1;j<=n;j++)//注意这里j的循环开始值，不能是C+1，因为这样会使得后面推的时候出现未计算的项

        {

            F[i][j][0]=min(F[i+1][j][0]+(D[i+1]-D[i])*(Sum[n]-Sum[j]+Sum[i]),

                           F[i+1][j][1]+(D[j]-D[i])*(Sum[n]-Sum[j]+Sum[i]));

            F[i][j][1]=min(F[i][j-1][0]+(D[j]-D[i])*(Sum[n]-Sum[j-1]+Sum[i-1]),

                           F[i][j-1][1]+(D[j]-D[j-1])*(Sum[n]-Sum[j-1]+Sum[i-1]));

            //cout<<i<<" "<<j<<" "<<F[i][j][0]<<" "<<F[i][j][1]<<endl;

        }

    cout<<min(F[1][n][0],F[1][n][1])<<endl;

    return 0;

}