线性代数的本质与几何意义 03. 矩阵与线性变换 (3blue1brown 咪博士 图文注解版)

首先，恭喜你读到了咪博士的这篇文章。本文可以说是该系列最重要、最核心的文章。你对线性代数的一切困惑，根源就在于没有真正理解矩阵到底是什么。读完咪博士的这篇文章，你一定会有一种醍醐灌顶、豁然开朗的感觉！

咱们先来说说啥叫变换。本质上，变换就是函数。

例如，你输入一个向量[ 5  7 ] [57]，

经过某个变换（即函数）的作用之后，输出另一个向量[ 2  -3 ] [2−3]

既然，变换本质上就是函数，那为啥还要多搞出这样一个术语？

其实，“变换”这个词暗示了我们能够以某种方式可视化 输入—-输出 关系。它暗示我们要从向量运动的角度去理解。即，变换让向量从一个地方（对应输入向量），运动到了另一个地方（对应输出向量）。

我们说将变换作用于某个空间，意思是将该变换应用于空间中的每一个向量。

空间中的向量可以用一些规则分布的点来表示。

下面是变换前的样子，

下面是变换后的样子。

变换后，空间中的点（即向量）运动到了其他的位置上。

二维空间变换中，等间距的平行网格可以更好地展示变换的性质。

下面是变换前的网格。

下面是变换后的网格。

显然，变换让空间发生了扭曲。

为了方便观察，我们还可以把变换前后的网格都画在同一张图上。

变换有时非常地复杂。

例如，下面的几个例子：

所幸的是，我们在线性代数中讨论的线性变换，没有那么复杂，也更容易理解。

那么线性变换是什么意思呢？如果一个变换同时具有以下 2 条性质，则它是一个线性变换。

• 变换前后，所有的直线仍然是直线
• 变换前后，原点保持不变

换句话说，线性变换是原点不变，并使网络线保持平行且等距分布的变换。

那么，我们要如何描述一个线性变换呢？

以平面直接坐标系为例，假定我们有一个向量 v = [-1  2 ] v⃗ =[−12]。我们可以将它看成是 2 个基向量 i, j 的线性组合。线性组合的系数分别对应向量的 2 个分量。

在某个线性变换的作用下，i, j 以及 v 都运动到了新的位置。

线性变换前后网络线保持平行且等距分布，这一性质有一个重要的推论：线性变换后的 v 是变换后的 i 和 j 的线性组合，并且线性组合的系数和变换前一样（仍然是 -1 和 2）

i⃗ =[10],j⃗ =[01]

v⃗ =−1[1−2]+2[30]=[52]

事实上，我们只要知道线性变换之后，i, j 的位置（坐标），就可以计算出任意一个向量经过同样的线性变换之后的位置（坐标）。

这意味着，对于一个线性变换，我们只需要跟踪基向量在变换前后的变化，就可以掌握整个空间（即全部向量）的变化。我们将线性变换后的基向量坐标按列组合起来，可以拼接成一个矩阵。线性变换的全部信息便都包含在这个矩阵当中了。

那么，向量[ x  y ] [xy] 经过该线性变换之后，其新坐标的计算方法如下：

这一计算过程，我们可以用矩阵乘法来表达。将向量[ x  y ] [xy]  记作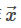x⃗ ，将整个矩阵记作 A，将线性变换后的向量记作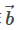,整个等式是不是变成了大家熟悉的

Ax⃗ =b⃗你可以把它看成是矩阵和向量相乘，也可以把它看成是一个线性方程组，现在你还可以把它看成是一个线性变换。多么奇妙的一件事啊！

一旦你理解的本节教程的精髓，你便可以秒懂原来看起来十分费解的线性变换。

例如，逆时针旋转 90 度对应的线性变换矩阵是什么呢？

记住，对于线性变换，我们只需要跟踪原来的基向量在线性变换后的位置（坐标），然后把它们按列拼成一个矩阵，这个矩阵就是相应的线性变换矩阵。

下面是一个剪切变换，你能一眼就看出它在做什么吗？

我们再来看下面这个线性变换，其线性变换矩阵的 2 个列向量是线性相关的。这个线性变换会将整个二维空间压缩到一条直线上。通过这个例子，你是不是对线性相关、线性无关有了更直观的、更深刻的认识了呢？

总之，线性变换是操纵空间的一种手段。线性变换保持原点不动，网格线平行且等距分布。只需要几个数字（变换后基向量的坐标）就可以清晰地描述一个线性变换。将变换后基向量的坐标按列拼接成一个矩阵。这个矩阵为我们提供了一种描述线性变换的语言。线性变换作用于一个向量，对应于用线性变换矩阵左乘该向量。

以后，当你再看到矩阵的时候，你都可以将它解读为对空间的某种线性变换，这是深刻理解矩阵乘法、行列式、基变换，以及特征值等概念的重要基础。掌握了本节（从线性变换的角度）看待矩阵的方式，线性代数中，原本极其抽象的概念，都将瞬间变得清晰起来。线性代数中各种看似莫名其妙的运算，以及各种神出鬼没的概念，一下子都变得可爱起来了。

原文链接：http://www.ipaomi.com/2017/11/24/线性代数的本质与几何意义-03-矩阵与线性变换-3blue1brown-咪/