noip2013火柴排队_Solution

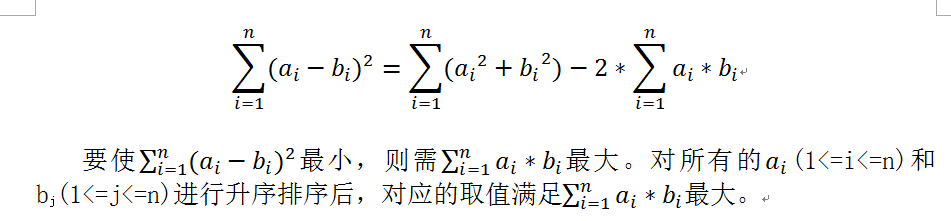
要想对任意(a_i，b_i)和(a_j­和b­_j)，当a_i<a_j时，都有b_i<=b_j；当a_i>=a_j时,b_i>=b_j,当对a进行升序排序后(b同时发生改变，从而不改变值，最后有a₁<=a₂<=…<=a_n)，必须满足b₁<=b₂<=…<=b­_n。

否则，必存在(a_i，b_i)和(a_j­和b­_j)，有a_i<a_j且b_i>b_j，交换a_i和a_j后，(a_j*b_i+ a_i*b_j)-( a_i*b_i+ a_j*b_j)=(a_j-a_i)*( b_i-b_j)>0，数值更小，即不是所满足的序列。

唯有满足条件“对任意(a_i，b_i)和(a_j­和b­_j)，当a_i<a_j时，都有b_i<=b_j；当a_i>=a_j时,b_i>=b_j”的序列才是值最小的序列。

最后目的是：对任意(a_i，b_i)和(a_j­和b­_j)，当a_i<a_j时，都有b_i<=b_j；当a_i>=a_j时,b_i>=b_j，其中题目限制“同一列火柴的高度互不相同”，所以对a,b序列进行从小到大排序，数的编号具有唯一性，即最后a，b两个序列中，a_i在a序列的编号等于b_i在b序列的编号。

每一次操作，一列(a,b数组)中相邻的两个数进行交换，其中a_i和a_i+1的交换等效于b_i和b_i+1的交换。我们可以固定a序列不动，修改b序列，最优的操作满足操作次数最少。

b序列第i位的数要移到目标位置第v_i位中，求出v序列。b序列的数的移动顺序是按照对应的v序列的数从小到大。当目标位置为第v_i位对应的b_i(原来)需要移动时，前面的第1~v_i-1位已经排好，而其它b_i(原来)前面的数为还未移动的数，即对应的v序列的值大于v_i。所以b_i(原来)需要向左移动的次数为满足j<i and v_j>v_i所有的j的个数。

即总的操作次数为v序列的逆序对的个数。有两种方法求逆序对使得时间复杂度为O(nlogn)：

1.归并排序+统计

2.离散化+树状数组

Code:

 #include <stdio.h>
 #include <stdlib.h>
 #include <math.h>
 #define yu 99999997
 #define maxn 100000
  
 struct node
 {
     long value,pos;
 }a[maxn+],b[maxn+];
 long v[maxn+],t[maxn+],ans;
  
 int cmp(const void *a,const void *b)
 {
     if ((*(struct node *)a).value<(*(struct node *)b).value)
         return -;
     else
         return ;
 }
  
 void mergesort(long l,long r)
 {
     if (l==r)
         return ;
     long mid,x,y,z,i;
     mid=(l+r)/;
     mergesort(l,mid);
     mergesort(mid+,r);
     for (i=l;i<=r;i++)
         t[i]=v[i];
     x=l;
     y=mid+;
     z=l;
     while (x<=mid && y<=r)
     {
         //两个数相等时让左边的数先加，因为相同的数不能凑成一对
         if (t[x]<=t[y])
         {
             v[z]=t[x];
             x++;
             //v[x] > v[mid+1]~v[y-1]
             ans=(ans+(y-mid-))%yu;
         }
         else if (t[x]>t[y])
         {
             v[z]=t[y];
             y++;
         }
         z++;
     }
     if (x<=mid)
     {
         //v[x] > v[mid+1]~v[r]
         ans=(ans+(mid-x+)*(r-mid))%yu;
         while (z<=r)
         {
             v[z]=t[x];
             x++;
             z++;
         }
     }
     else
     {
         while (z<=r)
         {
             v[z]=t[y];
             y++;
             z++;
         }
     }
 }
  
 int main()
 {
     long n,i;
     scanf("%ld",&n);
     for (i=;i<=n;i++)
     {
         scanf("%ld",&a[i].value);
         a[i].pos=i;
     }
     for (i=;i<=n;i++)
     {
         scanf("%ld",&b[i].value);
         b[i].pos=i;
     }
     qsort(a+,n,sizeof(struct node),cmp);
     qsort(b+,n,sizeof(struct node),cmp);
     for (i=;i<=n;i++)
         v[b[i].pos]=a[i].pos;
     ans=;
     mergesort(,n);
     printf("%ld\n",ans);
     return ;
 }
 /*
 Input:
 10
 10 1 5 2 7 4 9 3 6 8
 7 5 1 8 10 4 6 2 3 9
 Output:
 18
 */

感慨一下：想当初比赛做这道题，没有想到是逆序对，最终没有做出来，留下遗憾。现在终于写了个题解，把这道题做了，算是对遗憾的一种弥补吧。
希望自己可以走得更远……