CF1110G Tree-Tac-Toe 博弈论、构造

传送门

UPD：之前可能对白色变无色的过程讲的不是很清楚，已经补充

---

显然在双方绝顶聪明的情况下，黑色不可能赢

首先考虑树上一个白色的点都没有的情况：

1、如果树上有一个点的度数\(\geq 4\)，白色必赢，只需要第一次将这一个点染成白色，接着随便染它的两个邻居就可以达成目标

2、如果树上有一个点的度数\(=3\)，且它所连的\(3\)个点之间至少有\(2\)个点不是叶子节点，白色必赢，只需要第一次染这一个点，第二次染它的一个非叶子邻居，第三次就一定至少存在一个未被染色的点与这两个相邻。

那么剩下的情况，树的形态只会是下图中的三种

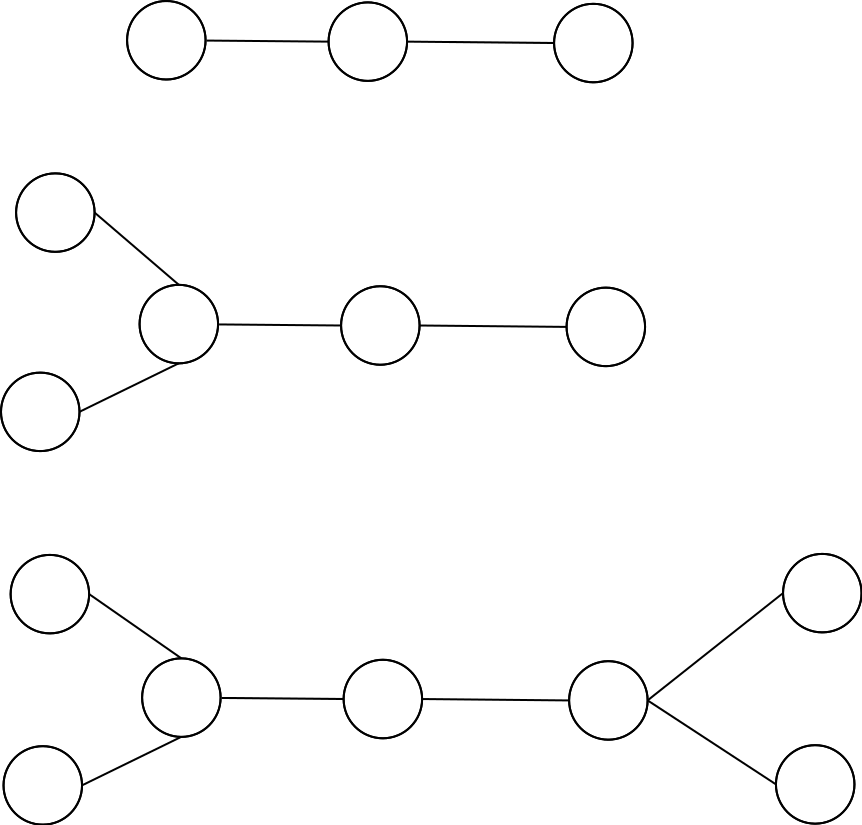
但是还没完（我以为到这里就完了结果WA2被Tutorial点名）

最重要的3、如果树的形态是上面的图中最下面的那一种，而且总点数为奇数，那么白色必赢

图长下面这样，中间的……省略的是一条链，编号从左往右递增。

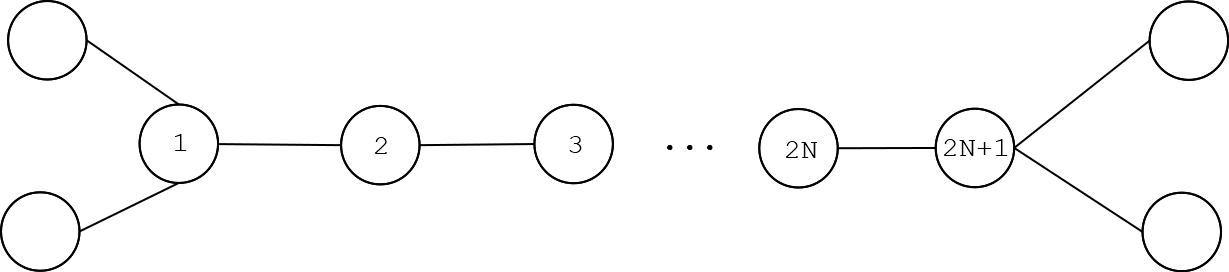
白色最开始染\(2\)号点，黑色如果染\(3\)号点白色直接染\(1\)号点，所以黑色必须染\(1\)号点。此时白色染\(4\)号点，黑色又只能染\(3\)号点……如是白色染到\(2N\)号点，黑色染\(2N-1\)号点之后，白色染\(2N+1\)号点，那么最右边就会有两个未被染的点，白色就赢了

其余的情况显然都是Draw的

然后考虑已经被染成白色的点的影响，最开始天真的我想直接各种特判过掉，结果WA14不晓得怎么回事

我们已经考虑了树上没有被染成白色的点的所有情况，那么能否将一个已经被染成白色的点等价为若干未被染成白色的点？实际上是可以的

假设下图中\(1\)号点在原树上是一个白色点，那就在保留它原来的邻居的基础上给它额外连上\(3\)个点，连成下面的\(ABCD\)结构

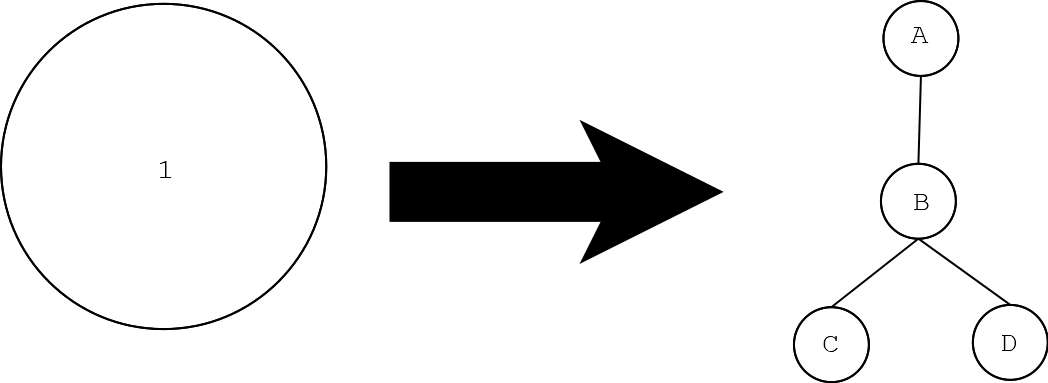
原图\(1\)号点对应新图的\(A\)号点，原图上\(1\)号点跟哪些点连了边，新图上\(A\)号点也和它们连边，然后在下面挂上\(BCD\)三个点

对于执白色的人来说，如果TA在某一回合涂白了\(A\)号点，这个时候如果执黑色者不涂黑\(B\)号点，那么执白色者将会在下一回合涂白\(B\)号点，对于\(CD\)两个点，白色就一定可以涂白其中一个，白色就赢了

所以执黑色者只能涂黑\(B\)号点。而这个时候\(BCD\)三个点对于胜负已经没有影响了，可以直接砍掉这三个点，就相当于白色直接涂白了\(A\)号点，也就是涂白了原图的\(1\)号点，然后又来到白色的回合。

#include<bits/stdc++.h>
//This code is written by Itst
using namespace std;

inline int read(){
    int a = 0;
    char c = getchar();
    bool f = 0;
    while(!isdigit(c)){
	    if(c == '-')
			f = 1;
        c = getchar();
    }
    while(isdigit(c)){
		a = (a << 3) + (a << 1) + (c ^ '0');
		c = getchar();
	}
	return f ? -a : a;
}

const int MAXN = 1e6 + 9;
struct Edge{
	int end , upEd;
}Ed[MAXN << 1];
int head[MAXN] , in[MAXN] , N , cntEd , cnt;
char s[MAXN];

inline void addEd(int a , int b){
	Ed[++cntEd].end = b;
	Ed[cntEd].upEd = head[a];
	head[a] = cntEd;
	++in[a];
}

int main(){
	for(int T = read() ; T ; --T){
		N = read();
		cntEd = 0;
		memset(head , 0 , sizeof(int) * (N + 1));
		memset(in , 0 , sizeof(int) * (N + 1));
		for(int i = 1 ; i < N ; ++i){
			int a = read() , b = read();
			addEd(a , b);
			addEd(b , a);
		}
		scanf("%s" , s + 1);
		if(N < 3){
		    puts("Draw");
		    continue;
		}
		if(N == 3){
		    int cnt = 0;
		    for(int i = 1 ; i <= N ; ++i)
		        cnt += s[i] == 'W';
		    puts(cnt >= 2 ? "White" : "Draw");
		    continue;
		}
		bool ifans = 0;
		int cnt1 = 0;
		for(int i = 1 ; i <= N ; ++i)
		    if(s[i] == 'W'){
		        addEd(i , ++N);
		        head[N] = 0;
		        addEd(N , i);
		        in[N] = 3;
		    }
		for(int i = 1 ; !ifans && i <= N ; ++i)
			if(in[i] > 3)
				ifans = 1;
			else
				if(in[i] == 3){
					int cnt = 0;
					for(int j = head[i] ; j ; j = Ed[j].upEd)
						cnt += in[Ed[j].end] >= 2;
					ifans = cnt >= 2;
					++cnt1;
			}
		if(cnt1 == 2 && (N & 1))
		    ifans = 1;
		puts(ifans ? "White" : "Draw");
	}
	return 0;
}