蓝桥杯近三年初赛题之二（16年b组）

1、

煤球数目

有一堆煤球，堆成三角棱锥形。具体：
第一层放1个，
第二层3个（排列成三角形），
第三层6个（排列成三角形），
第四层10个（排列成三角形），
....
如果一共有100层，共有多少个煤球？

请填表示煤球总数目的数字。
注意：你提交的应该是一个整数，不要填写任何多余的内容或说明性文字。

找规律，第n层是n-1层煤球的个数加上n，答案为：171700。代码如下：

 #include<stdio.h>
 int main()
 {
     int i,a[],s=;
     a[]=;
     for(i=;i<;i++)
         a[i]=a[i-]+i;
     for(i=;i<;i++)
     {
         s+=a[i];
         printf("%d ",a[i]);
     }
     printf("\n%d",s);
     return ;
 }

2、

生日蜡烛

某君从某年开始每年都举办一次生日party，并且每次都要吹熄与年龄相同根数的蜡烛。

现在算起来，他一共吹熄了236根蜡烛。

请问，他从多少岁开始过生日party的？

请填写他开始过生日party的年龄数。
注意：你提交的应该是一个整数，不要填写任何多余的内容或说明性文字。

一个二重循环暴力解决，答案为：26。代码如下：

 #include<stdio.h>
 int main()
 {
     int s,i,j;
     for(i=;i<;i++)
     {
         s=;
         for(j=i;j<;j++)
         {
             s+=j;
             if(s>)
                 break;
             if(s==)
                 printf("%d",i);
         }
     }
     return ;
 }

3、

凑算式

B      DEF
A + --- + ------- = 10
       C      GHI

这个算式中A~I代表1~9的数字，不同的字母代表不同的数字。

比如：
6+8/3+952/714 就是一种解法，
5+3/1+972/486 是另一种解法。

这个算式一共有多少种解法？

注意：你提交应该是个整数，不要填写任何多余的内容或说明性文字。

一个深搜解决，答案为29。代码如下：

#include<stdio.h>
int sum=;
int a[];
int vis[];
void dfs(int cur)
{
    int i;
    if(cur==)
    {
        int x1,x2;
        x1=a[]*(a[]*+a[]*+a[])+a[]*(a[]*+a[]*+a[]);
        x2=a[]*(a[]*+a[]*+a[]);
        if(a[]+x1/x2==&&x1%x2==)
        {
            for(i=;i<;i++)
            {
                printf("%d ",a[i]);
            }
            printf("\n");
            sum++;
        }
    }
    else for(i=;i<;i++)
    {
        if(!vis[i])
        {
            vis[i]=;
            a[cur]=i;
            dfs(cur+);
            vis[i]=;
        }
    }
}
int main()
{
    dfs();
    printf("%d",sum);
    return ;
}

4、

快速排序

排序在各种场合经常被用到。
快速排序是十分常用的高效率的算法。

其思想是：先选一个“标尺”，
用它把整个队列过一遍筛子，
以保证：其左边的元素都不大于它，其右边的元素都不小于它。

这样，排序问题就被分割为两个子区间。
再分别对子区间排序就可以了。

下面的代码是一种实现，请分析并填写划线部分缺少的代码。

#include <stdio.h>

void swap(int a[], int i, int j)
{
　　int t = a[i];
　　a[i] = a[j];
　　a[j] = t;
}

int partition(int a[], int p, int r)
{
　　int i = p;
　　int j = r + 1;
　　int x = a[p];
　　while(1){
　　　　while(i<r && a[++i]<x);
　　　　while(a[--j]>x);
　　　　if(i>=j) break;
　　　　swap(a,i,j);
　　}
　　______________________;
　　return j;
}

void quicksort(int a[], int p, int r)
{
　　if(p<r){
　　　　int q = partition(a,p,r);
　　　　quicksort(a,p,q-1);
　　　　quicksort(a,q+1,r);
　　}
}

int main()
{
　　int i;
　　int a[] = {5,13,6,24,2,8,19,27,6,12,1,17};
　　int N = 12;

　　quicksort(a, 0, N-1);

　　for(i=0; i<N; i++) printf("%d ", a[i]);
　　printf("\n");

　　return 0;
}

注意：只填写缺少的内容，不要书写任何题面已有代码或说明性文字。

快速排序，一个交换，答案为：swap(a,p,j)。

5、

抽签

X星球要派出一个5人组成的观察团前往W星。
其中：
A国最多可以派出4人。
B国最多可以派出2人。
C国最多可以派出2人。
....

那么最终派往W星的观察团会有多少种国别的不同组合呢？

下面的程序解决了这个问题。
数组a[] 中既是每个国家可以派出的最多的名额。
程序执行结果为：
DEFFF
CEFFF
CDFFF
CDEFF
CCFFF
CCEFF
CCDFF
CCDEF
BEFFF
BDFFF
BDEFF
BCFFF
BCEFF
BCDFF
BCDEF
....
(以下省略，总共101行)

#include <stdio.h>
#define N 6
#define M 5
#define BUF 1024

void f(int a[], int k, int m, char b[])
{
　　int i,j;

　　if(k==N){
　　　　b[M] = 0;
　　　　if(m==0) printf("%s\n",b);
　　　　return;
　　}

　　for(i=0; i<=a[k]; i++){
　　　　for(j=0; j<i; j++) b[M-m+j] = k+'A';
　　　　______________________; //填空位置
　　}
}
int main()
{
　　int a[N] = {4,2,2,1,1,3};
　　char b[BUF];
　　f(a,0,M,b);
　　return 0;
}

仔细阅读代码，填写划线部分缺少的内容。

注意：不要填写任何已有内容或说明性文字。

这题我是猜着写的，结果对了。答案为：f(a,k+1,m-i,b)。

6、

方格填数

如下的10个格子
     +--+--+--+
　  |    |    |    |
+--+--+--+--+
| 　|    |    |    |
+--+--+--+--+
| 　|　|    |
+--+--+--+

填入0~9的数字。要求：连续的两个数字不能相邻。
（左右、上下、对角都算相邻）

一共有多少种可能的填数方案？

请填写表示方案数目的整数。
注意：你提交的应该是一个整数，不要填写任何多余的内容或说明性文字。

一个深搜，但我条件没写对，答案是：1580。转一下别人的代码：

 #include <stdio.h>
 #include <math.h>
 int flag[][]; //表示哪些可以填数
 int mpt[][]; //填数
 bool visit[];
 int ans = ;
 void init()   //初始化
 {
     int i,j;
     for(i =  ; i <  ; i ++)
         for(j =  ; j <  ; j ++)
             flag[i][j] = ;
     flag[][] = ;
     flag[][] = ;
 }  

 void Solve()
 {
     int dir[][] = { ,,,-,,,-,,,,,-,-,,-,-};
     int book = true;
     for(int i =  ; i <  ; i ++)
     {
         for(int j =  ; j < ; j ++)
         {
             //判断每个数周围是否满足
             if(flag[i][j] == )continue;
             for( int k =  ; k <  ; k ++)
             {
                 int x,y;
                 x = i + dir[k][];
                 y = j + dir[k][];
                 if(x <  || x >=  || y <  || y >=  || flag[x][y] == ) continue;
                 if(abs(mpt[x][y] - mpt[i][j]) == )  book = false;
             }
         }
     }
     if(book) ans ++;
 }  

 void dfs(int index)
 {
     int x,y;
     x = index / ;
     y = index % ;
     if( x == )
     {
         Solve();
         return;
     }
     if(flag[x][y])
     {
         for(int i =  ; i <  ; i ++)
         {
             if(!visit[i])
             {
                 visit[i] = true;
                 mpt[x][y] = i;
                 dfs(index+);
                 visit[i] = false;
             }
         }
     }
     else
     {
         dfs(index+);
     }
 }
 int main()
 {
     init();
     dfs();
     printf("%d\n",ans);
     return ;
 } 

7、

剪邮票

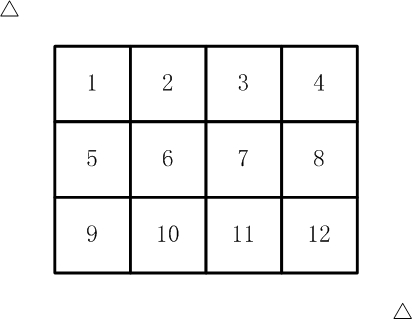
如【图1.jpg】, 有12张连在一起的12生肖的邮票。
现在你要从中剪下5张来，要求必须是连着的。
（仅仅连接一个角不算相连）
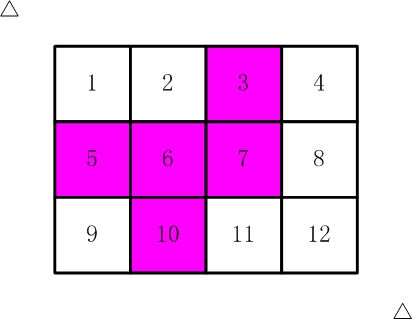
比如，【图2.jpg】，【图3.jpg】中，粉红色所示部分就是合格的剪取。

请你计算，一共有多少种不同的剪取方法。

请填写表示方案数目的整数。
注意：你提交的应该是一个整数，不要填写任何多余的内容或说明性文字。

同样是深搜，但我不会走格子，所以这一题我也GG了，答案为：116。转一下别人代码：

 #include <stdio.h>
 #include <string.h>
 int mpt[][];
 int mpt_visit[][];
 int num[];
 int have[];
 int visit[];
 int ans = ;
 int Count = ;  

 void init()
 {
     int k = ;
     for(int i =  ; i <  ; i ++)
         for(int j =  ; j <  ; j ++)
         {
             mpt[i][j] = k;
             k ++;
         }
 }
 int dir[][] = {,,,-,-,,,};
 //判断五个数是否能连在一起
 void dfs_find(int x,int y)
 {
     for(int i =  ; i <  ; i++)
     {
         int tx,ty;
         tx = x + dir[i][];
         ty = y + dir[i][];
         if(tx <  || tx >=  || ty <  || ty >= ) continue;
         if(have[mpt[tx][ty]] ==  || mpt_visit[tx][ty])continue;
         mpt_visit[tx][ty] = ;
         Count ++;
         dfs_find(tx,ty);
     }
 }  

 void Solve()
 {
     int i;
     memset(have,,sizeof(have));
     memset(mpt_visit,,sizeof(mpt_visit));
     for(i = ; i <  ; i ++) have[num[i]] = ;
     for(i =  ; i <  ; i ++)
     {
         int x,y;
         x = i / ;
         y = i % ;
         if(have[mpt[x][y]])
         {
             Count = ;
             mpt_visit[x][y] =;
             dfs_find(x,y);
             break;
         }
     }
     if(Count == )
     {
         ans ++;
     }
 }  

 //创建5个数的组合
 void dfs_creat(int index)
 {
     if(index == )
     {
         Solve();
         return;
     }
     for(int i = num[index-] + ; i <  ; i ++)
     {
         if(!visit[i])
         {
             visit[i] = true;
             num[index] = i;
             dfs_creat(index+);
             visit[i] = false;
         }
     }
 }  

 int main()
 {
     init();
     dfs_creat();
     printf("%d\n",ans);
     return ;
 } 

8、

四平方和

四平方和定理，又称为拉格朗日定理：
每个正整数都可以表示为至多4个正整数的平方和。
如果把0包括进去，就正好可以表示为4个数的平方和。

比如：
5 = 0^2 + 0^2 + 1^2 + 2^2
7 = 1^2 + 1^2 + 1^2 + 2^2
（^符号表示乘方的意思）

对于一个给定的正整数，可能存在多种平方和的表示法。
要求你对4个数排序：
0 <= a <= b <= c <= d
并对所有的可能表示法按 a,b,c,d 为联合主键升序排列，最后输出第一个表示法

程序输入为一个正整数N (N<5000000)
要求输出4个非负整数，按从小到大排序，中间用空格分开

例如，输入：
5
则程序应该输出：
0 0 1 2

再例如，输入：
12
则程序应该输出：
0 2 2 2

再例如，输入：
773535
则程序应该输出：
1 1 267 838

资源约定：
峰值内存消耗 < 256M
CPU消耗 < 3000ms

请严格按要求输出，不要画蛇添足地打印类似：“请您输入...” 的多余内容。

所有代码放在同一个源文件中，调试通过后，拷贝提交该源码。

注意: main函数需要返回0
注意: 只使用ANSI C/ANSI C++ 标准，不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include <xxx>， 不能通过工程设置而省略常用头文件。

提交时，注意选择所期望的编译器类型。

这题代码自己写的超时了，转一下别人O(n)的代码（先把两个平方数能相加的到的数字球出来然后记录）：

 #include <stdio.h>
 #include <math.h>
 int mpt[] ={};  //mpt[i] = 1表示i 能够用两个完全平方数相加而得。
 int n;
 void init()
 {
     for(int i =  ; i*i <= n ; i ++)
         for(int j =  ; j*j <=n ; j ++)
             if(i*i+j*j <= n) mpt[i*i+j*j] = ;
 }
 int main()
 {  

     int flag = false;
     scanf("%d",&n);
     init();
     for(int i =  ; i * i <= n ; i ++)
     {
         for(int j =  ; j * j <= n ; j ++){
             if(mpt[n - i*i - j*j] == ) continue;   //如果剩下的差用两个完全平方数不能组合出来就不继续
             for(int k =  ; k * k <= n ; k ++)
             {
                 int temp = n - i*i - j*j - k*k;
                 double l = sqrt((double) temp);
                 if(l == (int)l )
                 {
                     printf("%d %d %d %d\n",i,j,k,(int)l);
                     flag = true;
                     break;
                 }
             }
             if(flag)break;
         }
         if(flag)break;
     }
     return ;
 } 

9、

交换瓶子

有N个瓶子，编号 1 ~ N，放在架子上。

比如有5个瓶子：
2 1 3 5 4

要求每次拿起2个瓶子，交换它们的位置。
经过若干次后，使得瓶子的序号为：
1 2 3 4 5

对于这么简单的情况，显然，至少需要交换2次就可以复位。

如果瓶子更多呢？你可以通过编程来解决。

输入格式为两行：
第一行: 一个正整数N（N<10000）, 表示瓶子的数目
第二行：N个正整数，用空格分开，表示瓶子目前的排列情况。

输出数据为一行一个正整数，表示至少交换多少次，才能完成排序。

例如，输入：
5
3 1 2 5 4

程序应该输出：
3

再例如，输入：
5
5 4 3 2 1

程序应该输出：
2

资源约定：
峰值内存消耗 < 256M
CPU消耗 < 1000ms

请严格按要求输出，不要画蛇添足地打印类似：“请您输入...” 的多余内容。

所有代码放在同一个源文件中，调试通过后，拷贝提交该源码。

注意: main函数需要返回0
注意: 只使用ANSI C/ANSI C++ 标准，不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include <xxx>， 不能通过工程设置而省略常用头文件。

提交时，注意选择所期望的编译器类型。

自己的代码超时，同样转一下别人的代码：

#include <stdio.h>
#include <math.h>
int arr[];
int flag[];
int main()
{
    int ans = ;
    int n,i;
    scanf("%d",&n);
    for(i =  ; i <= n ; i ++) scanf("%d",&arr[i]);
    for(i =  ; i <= n ; i ++ )flag[arr[i]] = i;
    for(i =  ; i <= n ; i ++)
    {
        if( i != arr[i] )
        {
            int x = arr[i];
            arr[i] ^= arr[flag[i]] ^= arr[i] ^= arr[flag[i]];
            flag[i] ^= flag[x] ^= flag[i] ^= flag[x];
            ans ++;
        }
    }
    printf("%d\n",ans);
    return ;
}

10、

最大比例

X星球的某个大奖赛设了M级奖励。每个级别的奖金是一个正整数。
并且，相邻的两个级别间的比例是个固定值。
也就是说：所有级别的奖金数构成了一个等比数列。比如：
16,24,36,54
其等比值为：3/2

现在，我们随机调查了一些获奖者的奖金数。
请你据此推算可能的最大的等比值。

输入格式：
第一行为数字 N (0<N<100)，表示接下的一行包含N个正整数
第二行N个正整数Xi(Xi<1 000 000 000 000)，用空格分开。每个整数表示调查到的某人的奖金数额

要求输出：
一个形如A/B的分数，要求A、B互质。表示可能的最大比例系数

测试数据保证了输入格式正确，并且最大比例是存在的。

例如，输入：
3
1250 200 32

程序应该输出：
25/4

再例如，输入：
4
3125 32 32 200

程序应该输出：
5/2

再例如，输入：
3
549755813888 524288 2

程序应该输出：
4/1

资源约定：
峰值内存消耗 < 256M
CPU消耗 < 3000ms

请严格按要求输出，不要画蛇添足地打印类似：“请您输入...” 的多余内容。

所有代码放在同一个源文件中，调试通过后，拷贝提交该源码。

注意: main函数需要返回0
注意: 只使用ANSI C/ANSI C++ 标准，不要调用依赖于编译环境或操作系统的特殊函数。
注意: 所有依赖的函数必须明确地在源文件中 #include <xxx>， 不能通过工程设置而省略常用头文件。

提交时，注意选择所期望的编译器类型。

这题不会，具体思路移步至末尾他人blog，转一下他人代码：

 #include <stdio.h>
 #include <algorithm>
 #include <queue>
 using namespace std;
 #define LL long long
 struct fs
 {
     LL up,down;
 };
 int n;
 LL arr[];
 fs Fs[];  

 bool cmp(LL a,LL b)
 {
     return a > b;
 }  

 LL Gcd(LL a,LL b)
 {
     if( b ==  )return a;
     return Gcd(b,a%b);
 }
 LL Get(LL a, LL b)
 {
     if( a < b) a ^= b ^= a ^= b;
     LL v[];
     queue<LL>team;
     if( a == b || a / b == a) return b;
     v[] = a, v[] = b;
     v[] = a / b;
     int top = ,i,j;
     team.push(a/b);
     while(team.size())
     {
         LL now = team.front();
         team.pop();
         for(i =  ; i < top ; i ++)
         {
             LL temp = (v[i] > now) ? v[i] / now : now / v[i];
             bool find = false;
             for(j =  ; j < top ; j ++)
                 if( v[j] == temp) find = true;
             if(find == true) continue;
             team.push(temp);
             v[top++] = temp;
         }
     }
     LL ans = v[];
     for(i =  ; i < top ; i ++)
         if(v[i] != )
         {
             ans = v[i];
             break;
         }
     for(i =  ; i < top ; i ++)
         if( v[i] < ans && v[i] != ) ans = v[i];
     return ans;
 }
 int main()
 {
     int i,j;
     scanf("%d",&n);
     for(i =  ; i < n ; i ++) scanf("%lld",&arr[i]);
     sort(arr,arr+n,cmp);
     int top = ;
     for(i = ; i < n ; i ++)
         if(arr[i] != arr[i-]) arr[top++] = arr[i];
     n = top;
     for(i =  ; i < n - ; i ++)
     {
         LL gcd = Gcd(arr[i],arr[i+]);
         Fs[i].up = arr[i] / gcd;
         Fs[i].down = arr[i+] / gcd;
     }
     LL x = Fs[].up;
     for(i =  ; i < n -  ; i ++)
         x = Get(x,Fs[i].up);
     LL y = Fs[].down;
     for(i =  ; i < n - ; i ++)
         y = Get(y,Fs[i].down);
     printf("%lld/%lld\n",x,y);
     return ;
 } 

部分代码转自：https://blog.csdn.net/y1196645376/article/details/50938608