基2时域抽取FFT、IFFT的C++实现代码，另附DFT与IDFT的原始实现--转1

介绍
网络上的原理介绍非常丰富，具体请自行搜索网络资源。

本算法依靠FFT流图进行布置。

算法 ##
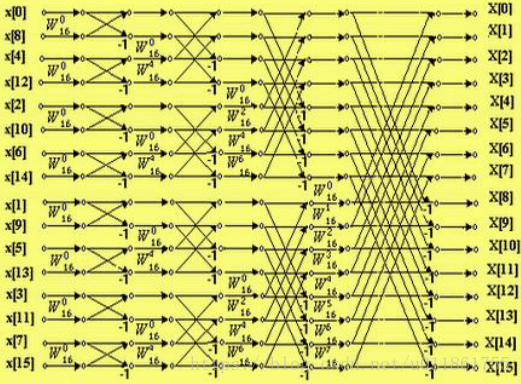
进行完所有的原理推导后，我们可以得到如下的16点FFT流图：

通过上图可以看出整个流图输入序列的顺序已经被颠倒，这实际上是输入序列中元素的序号进行了比特位的逆序排列，即其二进制比特位发生了镜像，例如001变为了100。另外一共有三个镶嵌的循环。

为了实现输入序列的比特逆序排列，要使用雷德算法进行实现。

下面进行FFT算法的核心讲解：

第一层循环：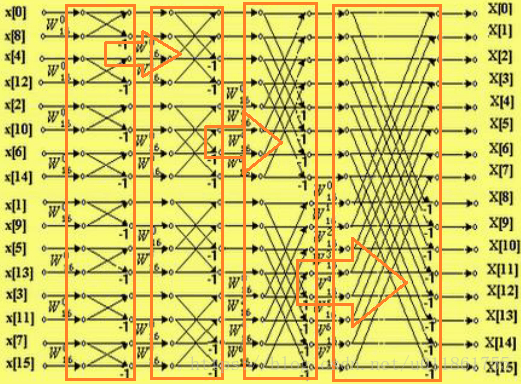

第二层循环：

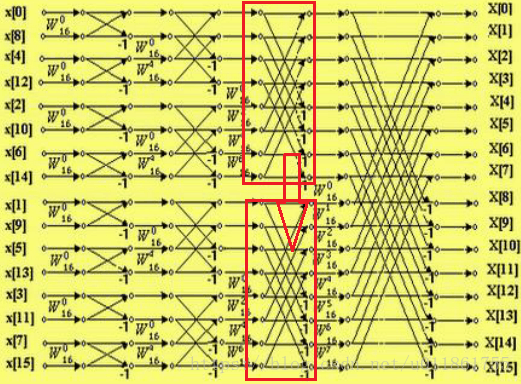
第三层循环：

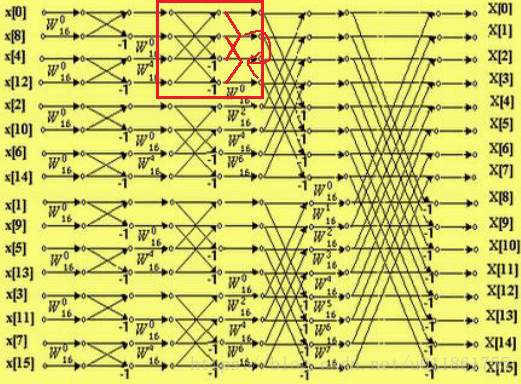
每一次循环中的蝴蝶运算操作请参阅网络资源。

FFT和IFFT的结果与DFT和IDFT的结果有一定的偏差，且由于计算机计算的精度关系，反变换结果与原始输入序列不一定完全相同。

下面给出代码：

#include <iostream>
#include <cmath>
#include <iomanip>
using namespace std;
double PI = 3.1415926535897933;
//定义复数结构体
typedef struct complex_number
{
    double real;
    double imagine;
}complex_number;
//定义旋转因子
complex_number omega_num(int k, int n, int input_length);
complex_number omega_num(int k, int n, int input_length)
{
    //k是傅里叶变换结果的序号
    //n是求解DFT时的序号
    //input_length是输入序列的长度
    complex_number omega_num;
    omega_num.real = cos(- * PI * k * n / input_length);
    omega_num.imagine = sin(- * PI * k * n / input_length);
    return omega_num;
}
//定义复数乘法的函数
complex_number complex_multiply(complex_number a, complex_number b);
complex_number complex_multiply(complex_number a, complex_number b)
{
    complex_number result;
    result.real = a.real*b.real - a.imagine*b.imagine;
    result.imagine = a.real*b.imagine + a.imagine*b.real;
    return result;
}
void main()
{
    //FFT - 快速傅里叶变换！
    //初始化 - 常量、变量的定义。
    const int input_length = ;//输入数组的长度
    double input[input_length] = { ,,, };
    //将输入数组进行比特倒位排列 - 雷德算法
    for (int j = , i = ; i < input_length - ; i++)//这里实现了奇偶前后分开排序
    {
        int k;
        if (i < j)//如果i<j,即进行变址
        {
            double temp;
            temp = input[j];
            input[j] = input[i];
            input[i] = temp;
        }
        k = input_length / ;//求j的下一个倒位序
        while (j >= k)//如果k<=j,表示j的最高位为1
        {
            j = j - k;//把最高位变成0
            k = k / ;//k/2，比较次高位，依次类推，逐个比较，直到某个位为0
        }
        j = j + k;
    }
    ////显示比特逆排序的结果
    //比特逆序数结束后，原输入序列已经发生改变~~~，如果要用原始DFT公式进行FFT的验算，则需要将原始输入序列重新定义。
 
    //核心部分：FFT迭代-------------------------------------------------------------------
    int EachLayer_length;//蝶形运算数量。每执行一次外循环时，每个区域的蝶形运算器的数量的2倍
    complex_number FFT_Output[input_length];
 
    //由于最底层的输入是实数，而输出也是实数，所以单独拿出来进行循环
    //最底层
    for (int a = ; a < input_length; a += )
    {
        double temp;
        temp = input[a];
        input[a] = input[a] + input[a + ];//注意这一步完成以后input[a]的值将改变，必须将原始input[a]的值放在临时变量中保存。
        input[a + ] = temp - input[a + ];
    }
    //显示最底层的计算结果
    //for (int i = 0; i < input_length; i++)
    //{
    //  cout << input[i] << endl;
    //}
 
    //将最底层计算出的结果全部赋值给FFT输出变量，即FFT_Output
    for (int b = ; b < input_length; b++)
    {
        FFT_Output[b].real = input[b];
        FFT_Output[b].imagine = ;
    }
    //从倒数第二层开始循环，保证所有的输入与输出都是复数
    for (int s = ; s <= log(input_length) / log(); s++)
    {
        EachLayer_length = (int)pow(, s);//每一次最外层循环时，每层的蝶形运算数量，是蝶形运算器数量的2倍。
        for (int m = ; m < input_length; m = m + EachLayer_length)
        {
            for (int n = ; n < EachLayer_length / ; n++)
            {
                complex_number temp;//定义临时复数变量。
                //蝶形运算
                temp.real = FFT_Output[m + n].real;
                temp.imagine = FFT_Output[m + n].imagine;
                FFT_Output[m + n].real = FFT_Output[m + n].real + complex_multiply(FFT_Output[m + n + EachLayer_length / ], omega_num(, n*input_length/( << s), input_length)).real;
                FFT_Output[m + n].imagine = FFT_Output[m + n].imagine + complex_multiply(FFT_Output[m + n + EachLayer_length / ], omega_num(, n*input_length / ( << s), input_length)).imagine;
                FFT_Output[m + n + EachLayer_length / ].real = temp.real - complex_multiply(FFT_Output[m + n + EachLayer_length / ], omega_num(, n*input_length / ( << s), input_length)).real;
                FFT_Output[m + n + EachLayer_length / ].imagine = temp.imagine - complex_multiply(FFT_Output[m + n + EachLayer_length / ], omega_num(, n*input_length / ( << s), input_length)).imagine;
            }
        }
    }
    EachLayer_length = ;//为后面的IFFT使用而将该变量置零。
    cout << "FFT变换结果为：\n";
    for (int q = ; q < input_length; q++)
    {
        if (FFT_Output[q].imagine < )
            cout << FFT_Output[q].real << FFT_Output[q].imagine << "i" << endl;
        else if (FFT_Output[q].imagine == )
            cout << FFT_Output[q].real << endl;
        else
            cout << FFT_Output[q].real << "+" << FFT_Output[q].imagine << "i" << endl;
    }
    cout << endl;
 
    //IFFT - 快速傅里叶逆变换！具体的循环原理请参照IFFT流图。
    //直接将FFT的输出结果作为输入，输入到FFT算法中，输出结果的实部就是IFFT的实序列。
    //定义需要使用的变量
    complex_number IFFT_Input[input_length];//IFFT的输入序列
    complex_number IFFT_Output[input_length];//IFFT的输出序列
    //将上文中FFT的计算结果全部赋给IFFT_Input，并对IFFT_Input的虚部取共轭;
    for (int a = ; a < input_length; a++)
    {
        IFFT_Input[a].real = FFT_Output[a].real;
        IFFT_Input[a].imagine = -FFT_Output[a].imagine;
    }
    //对输入的复数序列进行比特逆序排序 - 雷德算法
    //首先对输入序列的实数部分进行排序
    for (int j = , i = ; i < input_length - ; i++)
    {
        int k;
        if (i < j)
        {
            complex_number temp;
            temp = IFFT_Input[j];
            IFFT_Input[j] = IFFT_Input[i];
            IFFT_Input[i] = temp;
        }
        k = input_length / ;
        while (j >= k)
        {
            j = j - k;
            k = k / ;
        }
        j = j + k;
    }
    //核心部分：IFFT迭代，与FFT迭代一模一样-------------------------------------------------
    //从倒数第一层开始循环
    for (int s = ; s <= log(input_length) / log(); s++)
    {
        EachLayer_length = (int)pow(, s);//每一次最外层循环时，每层的蝶形运算数量，是蝶形运算器数量的2倍。
        for (int m = ; m < input_length; m = m + EachLayer_length)
        {
            for (int n = ; n < EachLayer_length / ; n++)
            {
                complex_number temp;//定义临时复数变量。
                //蝶形运算
                temp.real = IFFT_Input[m + n].real;
                temp.imagine = IFFT_Input[m + n].imagine;
                IFFT_Input[m + n].real = IFFT_Input[m + n].real + complex_multiply(IFFT_Input[m + n + EachLayer_length / ], omega_num(, n*input_length / ( << s), input_length)).real;
                IFFT_Input[m + n].imagine = IFFT_Input[m + n].imagine + complex_multiply(IFFT_Input[m + n + EachLayer_length / ], omega_num(, n*input_length / ( << s), input_length)).imagine;
                IFFT_Input[m + n + EachLayer_length / ].real = temp.real - complex_multiply(IFFT_Input[m + n + EachLayer_length / ], omega_num(, n*input_length / ( << s), input_length)).real;
                IFFT_Input[m + n + EachLayer_length / ].imagine = temp.imagine - complex_multiply(IFFT_Input[m + n + EachLayer_length / ], omega_num(, n*input_length / ( << s), input_length)).imagine;
            }
        }
    }
 
    //将计算完成的结果赋给输出序列IFFT_Output并显示结果
    cout << "IFFT结果：\n";
    for (int c = ; c < input_length; c++)
    {
        IFFT_Output[c].real = IFFT_Input[c].real / input_length;
        cout << IFFT_Output[c].real << endl;
    }
    cout << endl;
 
    //应用原始DFT公式对FFT算法进行验算
    const int input_length1 = ;
    double input1[input_length1] = { ,,, };
    complex_number DFT_sum, DFT_Output[input_length1];
    for (int k = ; k < input_length1; k++)
    {
        DFT_sum.real = DFT_sum.imagine = ;
        for (int n = ; n < input_length1; n++)
        {
            DFT_sum.real += input1[n] * omega_num(k, n, input_length1).real;
            DFT_sum.imagine += input1[n] * omega_num(k, n, input_length1).imagine;
        }
        DFT_Output[k].real = DFT_sum.real;
        DFT_Output[k].imagine = DFT_sum.imagine;
    }
    cout << "DFT变换结果为：\n";
    for (int q = ; q < input_length1; q++)
    {
        if (DFT_Output[q].imagine < )
            cout << DFT_Output[q].real << DFT_Output[q].imagine << "i" << endl;
        else if (DFT_Output[q].imagine == )
            cout << DFT_Output[q].real << endl;
        else
            cout << DFT_Output[q].real << "+" << DFT_Output[q].imagine << "i" << endl;
    }
    cout << endl;
 
    //下面进行IDFT
    double output_IDFT[input_length1], IDFT_sum;
    for (int n = ; n < input_length1; n++)
    {
        IDFT_sum = ;
        for (int k = ; k < input_length1; k++)
        {
            //这里一定注意复数与复数相乘的法则，不仅要将实数部分相乘，由于i*i=-1，所以还要减去虚数部分相乘的结果！
            IDFT_sum += DFT_Output[k].real*omega_num(k, -n, input_length1).real - DFT_Output[k].imagine*omega_num(k, -n, input_length1).imagine;
        }
        output_IDFT[n] = IDFT_sum / input_length1;
    }
    cout << "IDFT变换结果为：\n";
    for (int q = ; q < input_length1; q++)
        cout << output_IDFT[q] << endl;
    cout << endl;
}

---------------------
作者：WilliamS1995
来源：CSDN
原文：https://blog.csdn.net/u011861755/article/details/82666649
版权声明：本文为博主原创文章，转载请附上博文链接！