[solution] JZOJ-5795 词典

【solution】JZOJ-5795 词典

题面

Description

小C有$n$个字符串$T_1 T_n$，给出$m$个询问

第$i$个询问给出一个字符串$S_i$,对于每个询问，我们可以得到一个长度为$n$的$bool$数组$a$，其中$a_i=(S_i$是否为$T_i$的前缀$)$

例如，$a=[0,0,1]$表示$S_i$是$T_3$的前缀，但不是$T_1,T_2$的前缀。

对于每个询问给出的$a$数组，你的任务就是求出它最长的全$0$子串长度

Input

第一行两个数n,m，表示有n个字符串，m个询问。
接下来n行，每行一个字符串Ti 。
再接下来m行，每行一个字符串Si 。

Output

对于每个询问，输出一个ansi表示答案。

Sample Input

3 2
abcabc
aabc
abbc
aa
ba

Sample Output

1
3

Data Constraint

---

---

---

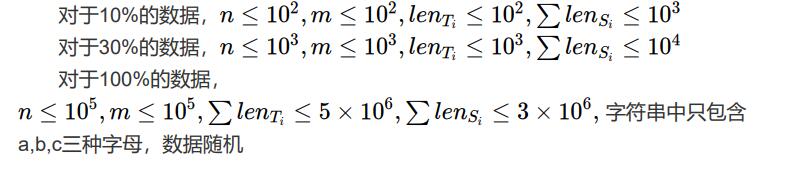
分割线

---

---

---

这是一个玄学的题目，有几种基于字典树（Trie）的做法，在考试的时候本蒟蒻在考场上一个小时一发手打出了数据不随机都没关系的在线做法，然鹅并没有什么卵用，统计的时候Trie爆了直接爆零

---

---

---

又是分割线

---

---

---

解法1：

这是一个离线做法（据说是标程？？？）

先读入数据（然鹅不用C++string难道不会爆数组吗）

再对查询建字典树，对模板串在字典树上跑一下，暴力求结果

解法2：

这貌似是一个在线的做法

对模板串建Trie，每次对询问串在字典树上跑一下，对下面的剩下部分暴力搜结果

这个的正确性就是因为数据是随机的，所以树高不会很大，因此就不会TLE了

正解来了！！！！

这是一个正常的玄学的做法，能够在不随机的数据上成功跑完，时间复杂度等于输入大小。考试的时候竟然被我想出来了（捂脸）

解题思路

对输入的模板串建一棵字典树，每个节点要存他的指向三个孩子的指针（这里用数组模拟），lst（上一次访问到这个节点的模板串编号，初始化为1），ans（这个节点的答案）。在每次添加模板串的时候暴力维护答案：如果当前访问的序号与上次的序号lst不相邻的话就用index-lst-1更新答案。在所有的模板串都添加完后再对所有的节点用n+1更新一下答案就可以了（这个很重要）。

查询的时候就把询问再字典树上跑一遍，如果不存在就直接输出n，存在的话就直接输出ans就好了

玄学的在线做法，复杂度是与输入规模相等的

121ms,119.50MB（主要是字典树节点）

（忽略注释掉的debug部分）

Code

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cstring>
#include<string>
#include<cmath>
#include<algorithm>
#define ll long long
#define maxn 1000005
using namespace std;
int n,m;
struct Trie{
	int num;
	int lst,ans;
	int nxt[3];
	Trie(){
		lst=0;
		ans=0;
		nxt[0]=-1;
		nxt[1]=-1;
		nxt[2]=-1;
	}
}node[maxn*5];
int tot=1;
char p[maxn*5];
int gmax(int a,int b){return a>b?a:b;}
void add(char a[],int index){
	int len=strlen(a),np=0;
	for(int i=0;i<len;i++){
		int nc=a[i]-'a';//cout<<nc<<' ';
		if(node[np].nxt[nc]==-1){
			node[np].nxt[nc]=tot;
			node[tot]=Trie();
			node[tot].num=nc;
			tot++;
			//cout<<index<<endl;
		}
		//if(nc==1) cout<<index<<' '<<node[np]<<endl;
		np=node[np].nxt[nc];
		int last=node[np].lst;
		if(index!=last+1){
			int cnt=index-last-1;
			node[np].ans=gmax(node[np].ans,cnt);
			//cout<<index<<endl;
		}
		node[np].lst=index;
	}
//cout<<endl;
	return;
}
void update(){
	int index=n+1;
	for(int i=1;i<tot;i++){
		int cnt=index-node[i].lst-1;
		node[i].ans=gmax(node[i].ans,cnt);
	}return;
}
int query(char a[]){
	int len=strlen(a),np=0;
	for(int i=0;i<len;i++){
		int c=a[i]-'a';
		if(node[np].nxt[c]==-1){
			return n;
		}
		else{
			np=node[np].nxt[c];
		}
	}
	//cout<<np<<' ';
	return node[np].ans;
}
int main(){
	freopen("word.in","r",stdin);
	freopen("word.out","w",stdout);
	scanf("%d %d",&n,&m);
	node[0]=Trie();
	for(int i=1;i<=n;i++){
		scanf("%s",p);
		add(p,i);
		//cout<<i<<' '<<node[480].ans<<endl;
	}
	update();
	for(int i=1;i<=m;i++){
		scanf("%s",p);
		printf("%d\n",query(p));
	}
	//for(int i=0;i<tot;i++){
	//	cout<<i<<' '<<node[i].nxt[0]<<' '<<node[i].nxt[1]<<' '<<node[i].nxt[2]<<endl;
	//}
	//cout<<tot<<endl;
	return 0;
}