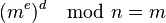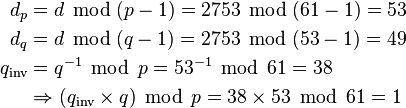RSA (cryptosystem)

https://en.wikipedia.org/wiki/RSA_(cryptosystem)

RSA is one of the first practical实用性的 public-key cryptosystems and is widely used for secure data transmission.

In such a cryptosystem密码系统, the encryption key is public and differs from the decryption key which is kept secret.  加密的key是公开的，解密的key是保密的

In RSA, this asymmetry不对称 is based on the practical difficulty of factoring因素 the product of two large prime numbers, the factoring problem.

RSA is made of the initial letters of the surnames of Ron Rivest, Adi Shamir, and Leonard Adleman, who first publicly described the algorithm in 1977.

Clifford Cocks, an English mathematician数学家 working for the UK intelligence agency情报机构 GCHQ, had developed an equivalent system in 1973, but it was not declassified撤销文件的机密等级 until 1997.^[1]

A user of RSA creates and then publishes a public key based on two large prime numbers, along with an auxiliary辅助的 value.

The prime numbers must be kept secret.

Anyone can use the public key to encrypt a message, but with currently published methods,

if the public key is large enough, only someone with knowledge of the prime numbers can feasibly切实 decode the message.^[2]

Breaking RSAencryption is known as the RSA problem; whether it is as hard as the factoring problem remains an open question.

RSA is a relatively slow algorithm, and because of this it is less commonly used to directly encrypt user data.

More often通常, RSA passes encrypted shared keys for symmetric对称的 key cryptography密码学；密码使用法 which in turn can perform bulk encryption-decryption operations at much higher speed.

Operation

The RSA algorithm involves four steps: key generation, key distribution, encryption and decryption.

RSA involves a public key and a private key. The public key can be known by everyone and is used for encrypting messages.

The intention is that messages encrypted with the public key can only be decrypted in a reasonable amount of time using the private key.

The basic principle behind RSA is the observation that it is practical to find three very large positive integers e,d and n such that with modular exponentiation  模幂运算for all m:

and that even knowing e and n or even m it can be extremely difficult to find d.

Additionally, for some operations it is convenient that the order of the two exponentiations can be changed and that this relation also implies:

Key distribution

To enable Bob to send his encrypted messages, Alice transmits her public key (n, e) to Bob via a reliable,可靠的 but not necessarily secret route路线, and keeps the private key d secret and this is never revealed透露 to anyone. Once distributed the keys can be reused over and over.

公钥(m,e)    私钥d

Bob用公钥将信息加密后，发送给Alice。  只有Alice自己知道私钥

Encryption

Bob then wishes to send message M to Alice.

He first turns M into an integer m, such that 0 ≤ m < n and gcd(m, n) = 1 by using an agreed-upon reversible可逆的 protocol known as a padding scheme.

He then computes the ciphertext密文 c, using the public key e of Alice, corresponding to

This can be done efficiently, even for 500-bit numbers, using modular exponentiation. Bob then transmits c to Alice.

Decryption

Alice can recover m from c by using her private key exponent d by computing

Given m, she can recover the original message M by reversing the padding scheme.

Key generation

The keys for the RSA algorithm are generated the following way:

1. Choose two distinct prime numbers p and q.
   • For security purposes, the integers p and q should be chosen at random, and should be similar in magnitude量级 but 'differ in length by a few digits'^[2] to make factoring harder. Prime integers can be efficiently found using aprimality test.
2. Compute n = pq.
   • n is used as the modulus模数 for both the public and private keys. Its length, usually expressed in bits, is the key length.
3. Compute φ(n) = φ(p)φ(q) = (p − 1)(q − 1) = n − (p + q − 1), where φ is Euler's totient function. This value is kept private.
4. Choose an integer d such that 1 < d < φ(n) and gcd(d, φ(n)) = 1; i.e., d and φ(n) are coprime.
5. Determine e as e ≡ d⁻¹ (mod φ(n)); i.e., e is the modular multiplicative inverse of d (modulo φ(n))

• This is more clearly stated as: solve for e given d⋅e ≡ 1 (mod φ(n))
• e having a short bit-length and small Hamming weight results in more efficient encryption – most commonly 2¹⁶ + 1 = 65,537. However, much smaller values of e (such as 3) have been shown to be less secure in some settings.^[13]
• e is released as the public key exponent.
• d is kept as the private key exponent.

The public key consists of the modulus n and the public (or encryption) exponent e. The private key consists of the modulus n and the private (or decryption) exponent d, which must be kept secret. p, q, and φ(n) must also be kept secret because they can be used to calculate d.

• An alternative, used by PKCS#1, is to choose d matching de ≡ 1 (mod λ) with λ = lcm(p − 1, q − 1), where lcm is the least common multiple. Using λ instead of φ(n) allows more choices for d. λ can also be defined using theCarmichael function, λ(n).

Since any common factors of (p-1) and (q-1) are present in the factorisation of p*q-1,^[14] it is recommended that (p-1) and (q-1) have only very small common factors, if any besides the necessary 2.^[15][2][16]

Example

Here is an example of RSA encryption and decryption. The parameters used here are artificially small, but one can also use OpenSSL to generate and examine a real keypair.

1. Choose two distinct prime numbers, such as

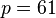    and 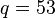          //233*9001

2. Compute n = pq giving

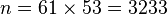                 //2097233

3. Compute the totient欧拉函数 of the product as φ(n) = (p − 1)(q − 1) giving

             //2088000

4. Choose any number 1 < d < 3120 that is coprime  互质 to 3120.

Choosing a prime number for d leaves us only to check that d is not a divisor因子 of 3120.

Let 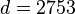       //d不能是3120的因子                                

5.Compute e, the modular multiplicative inverse of d (mod φ(n)) yielding,       2753*e%3120=1;

Worked example for the modular multiplicative inverse:     通过计算得到e

                                d*7%2088000=1;求出d=1193143

The public key is (n = 3233, e = 17). For a padded plaintext没有加密过的文件 message m, the encryption function is

 用公钥对m进行加密   

The private key is (d = 2753). For an encrypted ciphertext密文 c, the decryption function is

用私钥对c进行解密                      

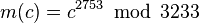
For instance, in order to encrypt m = 65, we calculate

     对65进行加密，65^17%3233=

To decrypt c = 2790, we calculate

      对2790进行解密,2790^2753%3233

Both of these calculations can be computed efficiently using the square-and-multiply algorithm for modular exponentiation.

In real-life situations the primes selected would be much larger;

in our example it would be trivial to factor n, 3233 (obtained from the freely available public key) back to the primes p and q.

Given e, also from the public key, we could then compute d and so acquire the private key.

Practical implementations use the Chinese remainder theorem to speed up the calculation using modulus of factors (mod pq using mod p and mod q).

The values d_p, d_q and q_inv, which are part of the private key are computed as follows:

Here is how d_p, d_q and q_inv are used for efficient decryption. (Encryption is efficient by choice of a suitable d and e pair)

RSA Public Key: (N, 7)    公钥的两个参数应该是(m,e)   
N = 233 * M     //p=233   q=9001     232*9000=2088000

RSA的公钥  (2097233,7)      Modulus=2097233 Exponent=7

a密文是197372，对其解密

b密文是333079，对其解密

d*e%((233-1)(9001-1))

=d*7%2088000=1

 for(int i = ; i <= ; i++)
                {
                    if(i*% == )
                    {
                        Console.WriteLine(i);
                        break;
                    }
                }

打印结果：1193143，所以d=1193143

a密文是197372，对其解密      a=197372^1193143mod2097233

b密文是333079，对其解密      b=333079^1193143mod2097233

https://www.cs.drexel.edu/~jpopyack/IntroCS/HW/RSAWorksheet.html

https://www.cs.drexel.edu/~introcs/Fa11/notes/10.1_Cryptography/RSA_Express_EncryptDecrypt.html

http://extranet.cryptomathic.com/rsacalc/index

                BigInteger number = ;
                int exponent = ;
                BigInteger modulus = ;
                Console.WriteLine("({0}^{1}) Mod {2} = {3}",
                                  number, exponent, modulus,
                                  BigInteger.ModPow(number, exponent, modulus));

a=378

b=390696