卡尔曼滤波— Constant Velocity Model

假设你开车进入隧道，GPS信号丢失，现在我们要确定汽车在隧道内的位置。汽车的绝对速度可以通过车轮转速计算得到，汽车朝向可以通过yaw rate sensor(A yaw-rate sensor is a gyroscopic device that measures a vehicle’s angular velocity around its vertical axis. )得到，因此可以获得X轴和Y轴速度分量Vx，Vy

首先确定状态变量，恒速度模型中取状态变量为汽车位置和速度：

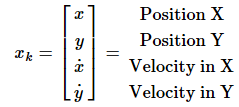
根据运动学定律(The basic idea of any motion models is that a mass cannot move arbitrarily due to inertia)：

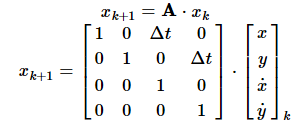
由于GPS信号丢失，不能直接测量汽车位置，则观测模型为：

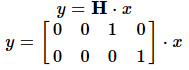
卡尔曼滤波步骤如下图所示：

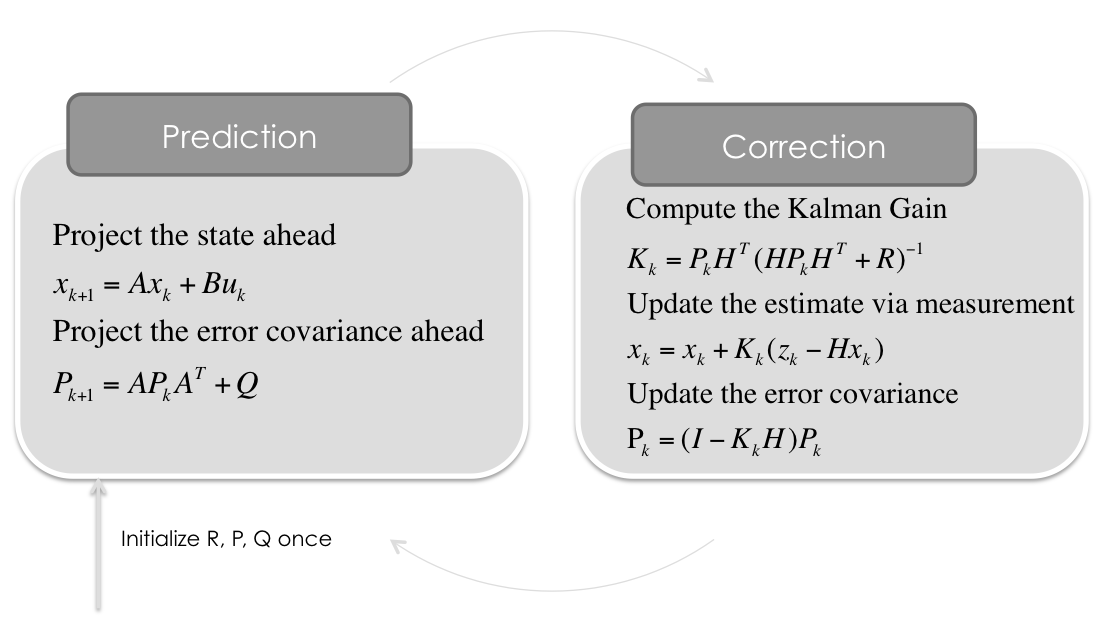
 # -*- coding: utf-8 -*-
 import numpy as np
 import matplotlib.pyplot as plt

 # Initial State x0
 x = np.matrix([[0.0, 0.0, 0.0, 0.0]]).T

 # Initial Uncertainty P0
 P = np.diag([1000.0, 1000.0, 1000.0, 1000.0])

 dt = 0.1 # Time Step between Filter Steps

 # Dynamic Matrix A
 A = np.matrix([[1.0, 0.0, dt, 0.0],
               [0.0, 1.0, 0.0, dt],
               [0.0, 0.0, 1.0, 0.0],
               [0.0, 0.0, 0.0, 1.0]])

 # Measurement Matrix
 # We directly measure the velocity vx and vy
 H = np.matrix([[0.0, 0.0, 1.0, 0.0],
               [0.0, 0.0, 0.0, 1.0]])

 # Measurement Noise Covariance
 ra = 10.0**2
 R = np.matrix([[ra, 0.0],
               [0.0, ra]])

 # Process Noise Covariance
 # The Position of the car can be influenced by a force (e.g. wind), which leads
 # to an acceleration disturbance (noise). This process noise has to be modeled
 # with the process noise covariance matrix Q.
 sv = 8.8
 G = np.matrix([[0.5*dt**2],
                [0.5*dt**2],
                [dt],
                [dt]])
 Q = G*G.T*sv**2

 I = np.eye(4)

 # Measurement
 m = 200 # 200个测量点
 vx= 20  # in X
 vy= 10  # in Y
 mx = np.array(vx+np.random.randn(m))
 my = np.array(vy+np.random.randn(m))
 measurements = np.vstack((mx,my))

 # Preallocation for Plotting
 xt = []
 yt = []

 # Kalman Filter
 for n in range(len(measurements[0])):

     # Time Update (Prediction)
     # ========================
     # Project the state ahead
     x = A*x

     # Project the error covariance ahead
     P = A*P*A.T + Q

     # Measurement Update (Correction)
     # ===============================
     # Compute the Kalman Gain
     S = H*P*H.T + R
     K = (P*H.T) * np.linalg.pinv(S)

     # Update the estimate via z
     Z = measurements[:,n].reshape(2,1)
     y = Z - (H*x)                            # Innovation or Residual
     x = x + (K*y)

     # Update the error covariance
     P = (I - (K*H))*P

     # Save states for Plotting
     xt.append(float(x[0]))
     yt.append(float(x[1]))

 # State Estimate: Position (x,y)
 fig = plt.figure(figsize=(16,16))
 plt.scatter(xt,yt, s=20, label='State', c='k')
 plt.scatter(xt[0],yt[0], s=100, label='Start', c='g')
 plt.scatter(xt[-1],yt[-1], s=100, label='Goal', c='r')

 plt.xlabel('X')
 plt.ylabel('Y')
 plt.title('Position')
 plt.legend(loc='best')
 plt.axis('equal')
 plt.show()

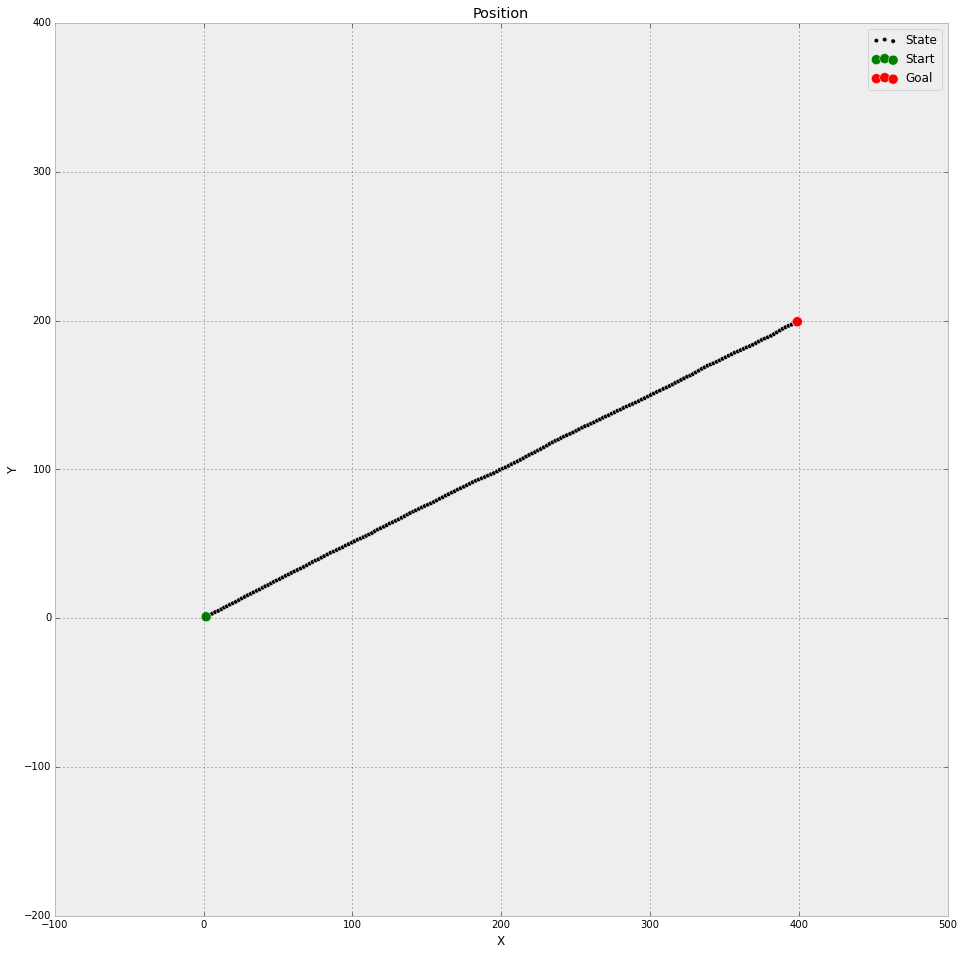
汽车在隧道中的估计位置如下图：

参考

Improving IMU attitude estimates with velocity data

https://zhuanlan.zhihu.com/p/25598462