poj 3734 矩阵快速幂+YY

题目原意：N个方块排成一列，每个方块可涂成红、蓝、绿、黄。问红方块和绿方块都是偶数的方案的个数。

sol：找规律列递推式+矩阵快速幂

设已经染完了i个方块将要染第i+1个方块。

a[i]=1-i方块中，红、绿方块数量都是偶数的方案数

b[i]=1-i方块中，红、绿方块数量一个是偶数一个是奇数的方案数（红even绿odd 或 红odd绿even）

c[i]=1-i方块中，红、绿方块数量都是奇数的方案数

可以得出递推公式：

a[i+1]=2*a[i]+b[i]　　　　

b[i+1]=2*a[i]+2*b[i]+2*c[i]

c[i+1]=b[i]+2*c[i]

如何和矩阵结合起来呢？不妨把公式这样写一遍，

a[i+1]=2*a[i]+1*b[i]+0*c[i]　　　　

b[i+1]=2*a[i]+2*b[i]+2*c[i]

c[i+1]=0*a[i]+1*b[i]+2*c[i]

然后可以YY出一个矩阵：

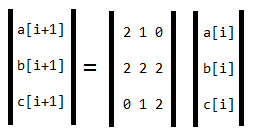
因此，

这样就可以用矩阵快速幂求解了。

 #include "iostream"
 #include "vector"
 #include "cstring"
 using namespace std;
 
 typedef unsigned long int ULL;
 typedef vector<ULL> vec;
 typedef vector<vec> mat;
 const ULL P=;
 int n,m;
 
 mat mul(mat &A,mat &B)      //return A*B
 {
     mat C(A.size(),vec(B[].size()));
     for (int i=;i<(int)A.size();i++)
     {
         for (int k=;k<(int)B.size();k++)
         {
             for (int j=;j<(int)B[].size();j++)
             {
                 C[i][j]=(C[i][j]+A[i][k]*B[k][j])%P;
             }
         }
     }
     return C;
 }
 
 mat m_pow(mat A,int m)      //return A^m
 {
     mat B(A.size(),vec(A.size()));
     for (int i=;i<(int)A.size();i++)
         B[i][i]=;
     while (m>)
     {
         if (m&)    B=mul(B,A);
         A=mul(A,A);
         m>>=;
     }
     return B;
 }
 
 int main()
 {
     int T,N;
     cin>>T;
     while (T--)
     {
         cin>>N;
         mat A(,vec());
         A[][]=;  A[][]=;  A[][]=;
         A[][]=;  A[][]=;  A[][]=;
         A[][]=;  A[][]=;  A[][]=;
 
         A=m_pow(A,N);
 
         cout<<A[][]<<endl;
     }
     return ;
 }
 
 /*
 int main()
 {
     int T;
     cin>>T;
     while (T--)
     {
         cin>>n>>m;
         mat A(n,vec(n));
 
         for (int i=0;i<n;i++)
             for (int j=0;j<n;j++)
                 cin>>A[i][j];
 
         A=m_pow(A,m);
 
         ULL ans=0;
         for (int i=0;i<n;i++)
         {
             ans+=A[i][i];
             ans=ans%P;
         }
         cout<<ans<<endl;
     }
     return 0;
 }
 */