DPM总结

• DPM：Deformable Parts Model（来自http://www.cs.berkeley.edu/~rbg/latent/index.html）

目标检测算法

先计算梯度方向直方图，在用SVM训练检测模型，然后是模型检测图像。

是在HOG模型的基础上修改得到的，HOG训练出来的是一个模型，模型内的子模型是没有偏移的，而DPM将模型的子模型是可移动的，并且移动的位移有限。比如使用对得到的人体的HOG，这个模型包含头部、四肢和身体等四个子模型，不同图片上人的姿势体现了子模型的可移动性。（也称之为弹簧形变模型）。

• HOG（Histogram of Oriented Gradient）梯度方向直方图

是一种解决人体目标检测的图像描述子，该方法使用HOG特征表达人体，提取人体的外形信息和运动信息，形成丰富的特征集。

下文是转自文章http://www.cnblogs.com/tiandsp/archive/2013/05/24/3097503.html （谢谢作者）

HOG（Histogram of Oriented Gradient）方向梯度直方图，主要用来提取图像特征，最常用的是结合svm进行行人检测。

算法流程图如下（这篇论文上的）：

下面我再结合自己的程序，表述一遍吧：

1.对原图像gamma校正，img=sqrt(img);

2.求图像竖直边缘，水平边缘，边缘强度，边缘斜率。

3.将图像每16*16（取其他也可以）个像素分到一个cell中。对于256*256的lena来说，就分成了16*16个cell了。

4.对于每个cell求其梯度方向直方图。通常取9（取其他也可以）个方向（特征），也就是每360/9=40度分到一个方向，方向大小按像素边缘强度加权。最后归一化直方图。

5.每2*2（取其他也可以）个cell合成一个block，所以这里就有（16-1）*（16-1）=225个block。

6.所以每个block中都有2*2*9个特征，一共有225个block，所以总的特征有225*36个。

当然一般HOG特征都不是对整幅图像取的，而是对图像中的一个滑动窗口取的。

lena图：

求得的225*36个特征：

matlab代码如下：

clear all; close all; clc;
img=double(imread('lena.jpg'));
imshow(img,[]);
[m n]=size(img);
img=sqrt(img);      %伽马校正
%下面是求边缘
fy=[-1 0 1];        %定义竖直模板
fx=fy';             %定义水平模板
Iy=imfilter(img,fy,'replicate');    %竖直边缘
Ix=imfilter(img,fx,'replicate');    %水平边缘
Ied=sqrt(Ix.^2+Iy.^2);              %边缘强度
Iphase=Iy./Ix;              %边缘斜率，有些为inf,-inf,nan，其中nan需要再处理一下

%下面是求cell
step=16;                %step*step个像素作为一个单元
orient=9;               %方向直方图的方向个数
jiao=360/orient;        %每个方向包含的角度数
Cell=cell(1,1);              %所有的角度直方图,cell是可以动态增加的，所以先设了一个
ii=1;
jj=1;
for i=1:step:m          %如果处理的m/step不是整数，最好是i=1:step:m-step
    ii=1;
    for j=1:step:n      %注释同上
        tmpx=Ix(i:i+step-1,j:j+step-1);
        tmped=Ied(i:i+step-1,j:j+step-1);
        tmped=tmped/sum(sum(tmped));        %局部边缘强度归一化
        tmpphase=Iphase(i:i+step-1,j:j+step-1);
        Hist=zeros(1,orient);               %当前step*step像素块统计角度直方图,就是cell
        for p=1:step
            for q=1:step
                if isnan(tmpphase(p,q))==1  %0/0会得到nan，如果像素是nan，重设为0
                    tmpphase(p,q)=0;
                end
                ang=atan(tmpphase(p,q));    %atan求的是[-90 90]度之间
                ang=mod(ang*180/pi,360);    %全部变正，-90变270
                if tmpx(p,q)<0              %根据x方向确定真正的角度
                    if ang<90               %如果是第一象限
                        ang=ang+180;        %移到第三象限
                    end
                    if ang>270              %如果是第四象限
                        ang=ang-180;        %移到第二象限
                    end
                end
                ang=ang+0.0000001;          %防止ang为0
                Hist(ceil(ang/jiao))=Hist(ceil(ang/jiao))+tmped(p,q);   %ceil向上取整，使用边缘强度加权
            end
        end
        Hist=Hist/sum(Hist);    %方向直方图归一化
        Cell{ii,jj}=Hist;       %放入Cell中
        ii=ii+1;                %针对Cell的y坐标循环变量
    end
    jj=jj+1;                    %针对Cell的x坐标循环变量
end
%下面是求feature,2*2个cell合成一个block,没有显式的求block
[m n]=size(Cell);
feature=cell(1,(m-1)*(n-1));
for i=1:m-1
   for j=1:n-1
        f=[];
        f=[f Cell{i,j}(:)' Cell{i,j+1}(:)' Cell{i+1,j}(:)' Cell{i+1,j+1}(:)'];
        feature{(i-1)*(n-1)+j}=f;
   end
end
%到此结束，feature即为所求
%下面是为了显示而写的
l=length(feature);
f=[];
for i=1:l
    f=[f;feature{i}(:)'];
end
figure
mesh(f)

上文是转自文章http://www.cnblogs.com/tiandsp/archive/2013/05/24/3097503.html，谢谢作者分享

• SVM

下文来自：http://www.cnblogs.com/LeftNotEasy/archive/2011/05/02/basic-of-svm.html

一、线性分类器：

首先给出一个非常非常简单的分类问题（线性可分），我们要用一条直线，将下图中黑色的点和白色的点分开，很显然，图上的这条直线就是我们要求的直线之一（可以有无数条这样的直线）

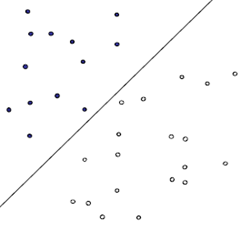    假如说，我们令黑色的点 = -1， 白色的点 =  +1，直线f(x) = w.x + b，这儿的x、w是向量，其实写成这种形式也是等价的f(x) = w1x1 + w2x2 … + wnxn + b, 当向量x的维度=2的时候，f(x) 表示二维空间中的一条直线， 当x的维度=3的时候，f(x) 表示3维空间中的一个平面，当x的维度=n > 3的时候，表示n维空间中的n-1维超平面。这些都是比较基础的内容，如果不太清楚，可能需要复习一下微积分、线性代数的内容。

刚刚说了，我们令黑色白色两类的点分别为+1, -1，所以当有一个新的点x需要预测属于哪个分类的时候，我们用sgn(f(x))，就可以预测了，sgn表示符号函数，当f(x) > 0的时候，sgn(f(x)) = +1, 当f(x) < 0的时候sgn(f(x)) = –1。

但是，我们怎样才能取得一个最优的划分直线f(x)呢？下图的直线表示几条可能的f(x)

一个很直观的感受是，让这条直线到给定样本中最近的点最远，这句话读起来比较拗口，下面给出几个图，来说明一下：

第一种分法：

第二种分法：

这两种分法哪种更好呢？从直观上来说，就是分割的间隙越大越好，把两个类别的点分得越开越好。就像我们平时判断一个人是男还是女，就是很难出现分错的情况，这就是男、女两个类别之间的间隙非常的大导致的，让我们可以更准确的进行分类。在SVM中，称为Maximum Marginal，是SVM的一个理论基础之一。选择使得间隙最大的函数作为分割平面是由很多道理的，比如说从概率的角度上来说，就是使得置信度最小的点置信度最大（听起来很拗口），从实践的角度来说，这样的效果非常好，等等。这里就不展开讲，作为一个结论就ok了，:)

上图被红色和蓝色的线圈出来的点就是所谓的支持向量(support vector)。

    上图就是一个对之前说的类别中的间隙的一个描述。Classifier Boundary就是f(x)，红色和蓝色的线（plus plane与minus plane）就是support vector所在的面，红色、蓝色线之间的间隙就是我们要最大化的分类间的间隙。

这里直接给出M的式子：（从高中的解析几何就可以很容易的得到了，也可以参考后面Moore的ppt）

另外支持向量位于wx + b = 1与wx + b = -1的直线上，我们在前面乘上一个该点所属的类别y（还记得吗?y不是+1就是-1），就可以得到支持向量的表达式为：y(wx + b) = 1，这样就可以更简单的将支持向量表示出来了。

当支持向量确定下来的时候，分割函数就确定下来了，两个问题是等价的。得到支持向量，还有一个作用是，让支持向量后方那些点就不用参与计算了。这点在后面将会更详细的讲讲。

在这个小节的最后，给出我们要优化求解的表达式：

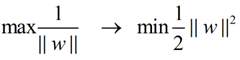
||w||的意思是w的二范数，跟上面的M表达式的分母是一个意思，之前得到，M = 2 / ||w||，最大化这个式子等价于最小化||w||, 另外由于||w||是一个单调函数，我们可以对其加入平方，和前面的系数，熟悉的同学应该很容易就看出来了，这个式子是为了方便求导。

这个式子有还有一些限制条件，完整的写下来，应该是这样的：（原问题）

s.t的意思是subject to，也就是在后面这个限制条件下的意思，这个词在svm的论文里面非常容易见到。这个其实是一个带约束的二次规划(quadratic programming, QP)问题，是一个凸问题，凸问题就是指的不会有局部最优解，可以想象一个漏斗，不管我们开始的时候将一个小球放在漏斗的什么位置，这个小球最终一定可以掉出漏斗，也就是得到全局最优解。s.t.后面的限制条件可以看做是一个凸多面体，我们要做的就是在这个凸多面体中找到最优解。这些问题这里不展开，因为展开的话，一本书也写不完。如果有疑问请看看wikipedia。

二、转化为对偶问题，并优化求解:

这个优化问题可以用拉格朗日乘子法去解，使用了KKT条件的理论，这里直接作出这个式子的拉格朗日目标函数：

求解这个式子的过程需要拉格朗日对偶性的相关知识（另外pluskid也有一篇文章专门讲这个问题），并且有一定的公式推导，如果不感兴趣，可以直接跳到后面用蓝色公式表示的结论，该部分推导主要参考自plukids的文章。

首先让L关于w，b最小化，分别令L关于w，b的偏导数为0，得到关于原问题的一个表达式

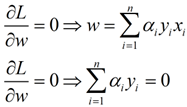
将两式带回L(w,b,a)得到对偶问题的表达式

新问题加上其限制条件是（对偶问题）:

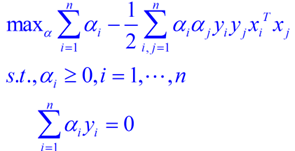
这个就是我们需要最终优化的式子。至此，得到了线性可分问题的优化式子。

求解这个式子，有很多的方法，比如SMO等等，个人认为，求解这样的一个带约束的凸优化问题与得到这个凸优化问题是比较独立的两件事情，所以在这篇文章中准备完全不涉及如何求解这个话题，如果之后有时间可以补上一篇文章来谈谈:)。

三、线性不可分的情况（软间隔）：

接下来谈谈线性不可分的情况，因为线性可分这种假设实在是太有局限性了：

下图就是一个典型的线性不可分的分类图，我们没有办法用一条直线去将其分成两个区域，每个区域只包含一种颜色的点。

     要想在这种情况下的分类器，有两种方式，一种是用曲线去将其完全分开，曲线就是一种非线性的情况，跟之后将谈到的核函数有一定的关系：

     另外一种还是用直线，不过不用去保证可分性，就是包容那些分错的情况，不过我们得加入惩罚函数，使得点分错的情况越合理越好。其实在很多时候，不是在训练的时候分类函数越完美越好，因为训练函数中有些数据本来就是噪声，可能就是在人工加上分类标签的时候加错了，如果我们在训练（学习）的时候把这些错误的点学习到了，那么模型在下次碰到这些错误情况的时候就难免出错了（假如老师给你讲课的时候，某个知识点讲错了，你还信以为真了，那么在考试的时候就难免出错）。这种学习的时候学到了“噪声”的过程就是一个过拟合（over-fitting），这在机器学习中是一个大忌，我们宁愿少学一些内容，也坚决杜绝多学一些错误的知识。还是回到主题，用直线怎么去分割线性不可分的点：

我们可以为分错的点加上一点惩罚，对一个分错的点的惩罚函数就是这个点到其正确位置的距离：

在上图中，蓝色、红色的直线分别为支持向量所在的边界，绿色的线为决策函数，那些紫色的线表示分错的点到其相应的决策面的距离，这样我们可以在原函数上面加上一个惩罚函数，并且带上其限制条件为：

公式中蓝色的部分为在线性可分问题的基础上加上的惩罚函数部分，当xi在正确一边的时候，ε=0，R为全部的点的数目，C是一个由用户去指定的系数，表示对分错的点加入多少的惩罚，当C很大的时候，分错的点就会更少，但是过拟合的情况可能会比较严重，当C很小的时候，分错的点可能会很多，不过可能由此得到的模型也会不太正确，所以如何选择C是有很多学问的，不过在大部分情况下就是通过经验尝试得到的。

接下来就是同样的，求解一个拉格朗日对偶问题，得到一个原问题的对偶问题的表达式：

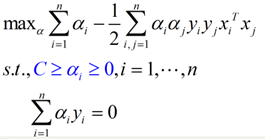
蓝色的部分是与线性可分的对偶问题表达式的不同之处。在线性不可分情况下得到的对偶问题，不同的地方就是α的范围从[0, +∞)，变为了[0, C]，增加的惩罚ε没有为对偶问题增加什么复杂度。

四、核函数：

刚刚在谈不可分的情况下，提了一句，如果使用某些非线性的方法，可以得到将两个分类完美划分的曲线，比如接下来将要说的核函数。

    我们可以让空间从原本的线性空间变成一个更高维的空间，在这个高维的线性空间下，再用一个超平面进行划分。这儿举个例子，来理解一下如何利用空间的维度变得更高来帮助我们分类的（例子以及图片来自pluskid的kernel函数部分）：

下图是一个典型的线性不可分的情况

但是当我们把这两个类似于椭圆形的点映射到一个高维空间后，映射函数为：

    用这个函数可以将上图的平面中的点映射到一个三维空间（z1,z2,z3)，并且对映射后的坐标加以旋转之后就可以得到一个线性可分的点集了。

用另外一个哲学例子来说：世界上本来没有两个完全一样的物体，对于所有的两个物体，我们可以通过增加维度来让他们最终有所区别，比如说两本书，从(颜色，内容)两个维度来说，可能是一样的，我们可以加上 作者 这个维度，是在不行我们还可以加入 页码，可以加入 拥有者，可以加入 购买地点，可以加入 笔记内容等等。当维度增加到无限维的时候，一定可以让任意的两个物体可分了。

回忆刚刚得到的对偶问题表达式：

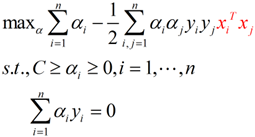
我们可以将红色这个部分进行改造，令：

     这个式子所做的事情就是将线性的空间映射到高维的空间,k(x, xj)有很多种，下面是比较典型的两种：

    上面这个核称为多项式核，下面这个核称为高斯核，高斯核甚至是将原始空间映射为无穷维空间，另外核函数有一些比较好的性质，比如说不会比线性条件下增加多少额外的计算量，等等，这里也不再深入。一般对于一个问题，不同的核函数可能会带来不同的结果，一般是需要尝试来得到的。

五、一些其他的问题：

1）如何进行多分类问题：

上面所谈到的分类都是2分类的情况，当N分类的情况下，主要有两种方式，一种是1 vs (N – 1)一种是1 vs 1，前一种方法我们需要训练N个分类器，第i个分类器是看看是属于分类i还是属于分类i的补集（出去i的N-1个分类）。

后一种方式我们需要训练N * (N – 1) / 2个分类器，分类器(i,j)能够判断某个点是属于i还是属于j。

这种处理方式不仅在SVM中会用到，在很多其他的分类中也是被广泛用到，从林教授（libsvm的作者）的结论来看，1 vs 1的方式要优于1 vs (N – 1)。

2）SVM会overfitting吗？

SVM避免overfitting，一种是调整之前说的惩罚函数中的C，另一种其实从式子上来看，min ||w||^2这个看起来是不是很眼熟？在最小二乘法回归的时候，我们看到过这个式子，这个式子可以让函数更平滑，所以SVM是一种不太容易over-fitting的方法。

参考文档：

主要的参考文档来自4个地方，wikipedia（在文章中已经给出了超链接了），pluskid关于SVM的博文，Andrew moore的ppt（文章中不少图片都是引用或者改自Andrew Moore的ppt，以及prml

上文来自http://www.cnblogs.com/LeftNotEasy/archive/2011/05/02/basic-of-svm.html

• SVM Matlab实验：

原文来自：http://blog.csdn.net/lwwangfang/article/details/52351715

1. 线性可分

function [ classification ] = SVM_L()
% 进行SVM线性可分的二分类处理
% 1、首先需要一组训练数据train，并且已知训练数据的类别属性，在这里，属性只有两类，并用1，2来表示。
% 2、通过svmtrain（只能处理2分类问题）函数，来进行分类器的训练
% 3、通过svmclassify函数，根据训练后获得的模型svm_struct，来对测试数据test进行分类
train=[0 0;2 4;3 3;3 4;4 2;4 4;4 3;5 3;6 2;7 1;2 9;3 8;4 6;4 7;5 6;5 8;6 6;7 4;8 4;10 10]; %训练数据点
group=[1,1,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2]'; %训练数据已知分类情况
%与train顺序对应
test=[3 2;4 8;6 5;7 6;2 5;5 2]; %测试数据

%训练分类模型
svmModel = svmtrain(train,group,'kernel_function','linear','showplot',true);

%分类测试
classification=svmclassify(svmModel,test,'Showplot',true);
end

2. 线性不可分

function [ classfication ] = SVM_NL()
%SVM对线性不可分的数据进行处理
%在选择核函数时，尝试用linear以外的rbf,quadratic,polynomial等，观察获得的分类情况
%训练数据
train=[5 5;6 4;5 6;5 4;4 5;8 5;8 8;4 5;5 7;7 8;1 2;1 4;4 2;5 1.5;7 3;10 4;4 9;2 8;8 9;8 10];
%训练数据分类情况
group=[1,1,1,1,1,1,1,1,1,1,2,2,2,2,2,2,2,2,2,2];
%测试数据
test=[6 6;5.5 5.5;7 6;12 14;7 11;2 2;9 9;8 2;2 6;5 10;4 7;7 4];

%训练分类模型
svmModel = svmtrain(train,group,'kernel_function','rbf','showplot',true);
%分类
classification=svmclassify(svmModel,test,'Showplot',true);
end

3. 利用多特征值实验

function [ classfication ] = SVM2_2()
%使用matlab自带的关于花的数据进行二分类实验（150*4），其中，每一行代表一朵花，
%共有150行（朵)，每一朵包含4个属性值（特征），即4列。且每1-50，51-100，101-150行的数据为同一类，分别为setosa青风藤类，versicolor云芝类，virginica锦葵类
%实验中为了使用svmtrain（只处理二分类问题）因此，将数据分为两类，51-100为一类，1-50和101-150共为一类
%实验先选用2个特征值，再选用全部四个特征值来进行训练模型，最后比较特征数不同的情况下分类精度的情况。

load fisheriris %下载数据包含：meas（150*4花特征数据）
%和species（150*1 花的类属性数据）
meas=meas(:,1:2); %选取出数据前100行，前2列
train=[(meas(51:90,:));(meas(101:140,:))]; %选取数据中每类对应的前40个作为训练数据
test=[(meas(91:100,:));(meas(141:150,:))];%选取数据中每类对应的后10个作为测试数据
group=[(species(51:90));(species(101:140))];%选取类别标识前40个数据作为训练数据

%使用训练数据，进行SVM模型训练
svmModel = svmtrain(train,group,'kernel_function','rbf','showplot',true);
%使用测试数据，测试分类效果
classfication = svmclassify(svmModel,test,'showplot',true);

%正确的分类情况为groupTest，实验测试获得的分类情况为classfication
groupTest=[(species(91:100));(species(141:150))];
%计算分类精度
count=0;
for i=(1:20)
if strcmp(classfication(i),groupTest(i))
count=count+1;
end
end
fprintf('分类精度为：%f\n' ,count/20);

end

• Pascal VOC Challenge简介：

Pattern Analysus， Statical Modeling and Computational Learning.

提供视觉分类识别和检测的一个基准测试，提供检测算法和学习性能的标准图像注释数据集和标准的评估系统。

VOC挑战提供两种参加形式，第一种仅用委员会所提供的数据，进行机器学习和训练。第二种是用测试之外的那些数据进行算法的训练。但两种情况必须严格的利用提供的测试数据来生成最终的结果。

VOC挑战赛主要分为三个部分：图像的分类、识别、分割，另外还有一个’动态‘分类项目。

分类是让算法找出测试图片都是属于哪一个标签，对测试图片进行分类，将图片对号入座。

检测是检测出测试图片中由委员会特别圈定的内容，看看算法能否正确的符合圈定的内容。

分割是对图片进行像素级分割，也就是识别出特定物体用一种颜色表示，其他的则作为背景。

动作分类则是在静态图片中预测人类的动作，比如有一张人类跑步的图片，算法根据身体各部分的位置特征判别这个动作是跑步。

人类轮廓识别是识别出人体的部位，这对于一张图片有多少个人或两个人身体部分纠缠在一起的图片识别有重要意义。