TarJan 算法求解有向连通图强连通分量

[有向图强连通分量]

在有向图G中，如果两个 顶点间至少存在一条路径，称两个顶点强连通(strongly connected)。如果有向图G的每两个顶点都强连通，称G是一个强连通图。非强连通图有向图的极大强连通子图，称为强连通分量(strongly connected components)。

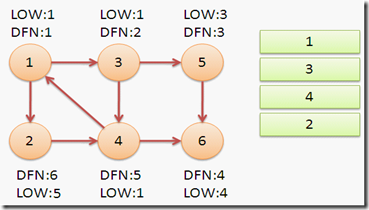
下图中，子图{1,2,3,4}为一个强连通分量，因为顶点1,2,3,4两两可达。{5},{6}也分别是两个强连通分量。

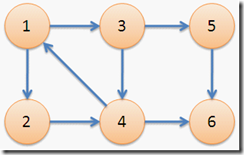
大体来说有3中算法Kosaraju,Trajan,Gabow这三种！后续文章中将相继介绍，首先介绍Tarjan算法

[Tarjan算法]

Tarjan算法是基于对图深度优先搜索的算法，每个强连通分量为搜索树中的一棵子树。搜索时，把当前搜索树中未处理的节点加入一个堆栈，回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。

定义DFN(u)为节点u搜索的次序编号(时间戳)，Low(u)为u或u的子树能够追溯到的最早的栈中节点的次序号。

算法伪代码如下

tarjan(u)
{

    DFN[u]=Low[u]=++Index     // 为节点u设定次序编号和Low初值

    Stack.push(u)                     // 将节点u压入栈中

    for each (u, v) in E               // 枚举每一条边

          if (v is not visted)          // 如果节点v未被访问过

                  tarjan(v)              // 继续向下找

                  Low[u] = min(Low[u], Low[v])

            else if (v in S)            // 如果节点v还在栈内

            Low[u] = min(Low[u], DFN[v])

    if (DFN[u] == Low[u])        // 如果节点u是强连通分量的根

       repeat

           v = S.pop                  // 将v退栈，为该强连通分量中一个顶点

           print v

      until (u== v)

} 

接下来是对算法流程的演示。

从节点1开始DFS，把遍历到的节点加入栈中。搜索到节点u=6时，DFN[6]=LOW[6]，找到了一个强连通分量。退栈到u=v为止，{6}为一个强连通分量。

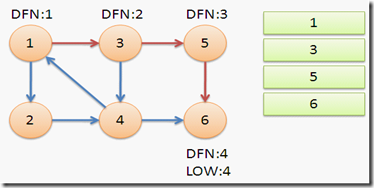
返回节点5，发现DFN[5]=LOW[5]，退栈后{5}为一个强连通分量。

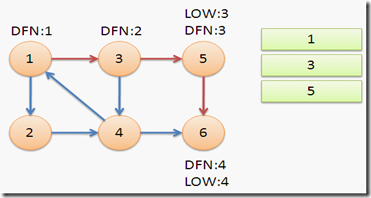
返回节点3，继续搜索到节点4，把4加入堆栈。发现节点4向节点1有后向边，节点1还在栈中，所以LOW[4]=1。节点6已经出栈，(4,6)是横叉边，返回3，(3,4)为树枝边，所以LOW[3]=LOW[4]=1。

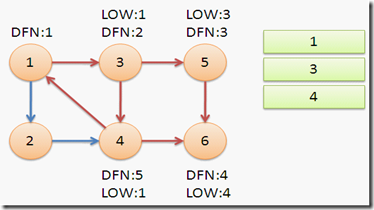
继续回到节点1，最后访问节点2。访问边(2,4)，4还在栈中，所以LOW[2]=DFN[4]=5。返回1后，发现DFN[1]=LOW[1]，把栈中节点全部取出，组成一个连通分量{1,3,4,2}。

至此，算法结束。经过该算法，求出了图中全部的三个强连通分量{1,3,4,2},{5},{6}。

可以发现，运行Tarjan算法的过程中，每个顶点都被访问了一次，且只进出了一次堆栈，每条边也只被访问了一次，所以该算法的时间复杂度为O(N+M)。

求 有向图的强连通分量还有一个强有力的算法，为Kosaraju算法。Kosaraju是基于对有向图及其逆图两次DFS的方法，其时间复杂度也是 O(N+M)。与Trajan算法相比，Kosaraju算法可能会稍微更直观一些。但是Tarjan只用对原图进行一次DFS，不用建立逆图，更简洁。 在实际的测试中，Tarjan算法的运行效率也比Kosaraju算法高30%左右。此外，该Tarjan算法与求无向图的双连通分量(割点、桥)的Tarjan算法也有着很深的联系。学习该Tarjan算法，也有助于深入理解求双连通分量的Tarjan算法，两者可以类比、组合理解。

求有向图的强连通分量的Tarjan算法是以其发明者Robert Tarjan命名的。Robert Tarjan还发明了求双连通分量的Tarjan算法，以及求最近公共祖先的离线Tarjan算法，在此对Tarjan表示崇高的敬意。

#include "cstdlib"
#include "cctype"
#include "cstring"
#include "cstdio"
#include "cmath"
#include "algorithm"
#include "vector"
#include "string"
#include "iostream"
#include "sstream"
#include "set"
#include "queue"
#include "stack"
#include "fstream"
#include "strstream"
using namespace std;

#define  M 2000              //题目中可能的最大点数
int STACK[M],top=;          //Tarjan 算法中的栈
bool InStack[M];             //检查是否在栈中
int DFN[M];                  //深度优先搜索访问次序
int Low[M];                  //能追溯到的最早的次序
int ComponetNumber=;        //有向图强连通分量个数
int Index=;                 //索引号
vector <int> Edge[M];        //邻接表表示
vector <int> Component[M];   //获得强连通分量结果

void Tarjan(int i)
{
    int j;
    DFN[i]=Low[i]=Index++;
    InStack[i]=true;
    STACK[++top]=i;
    for (int e=;e<Edge[i].size();e++)
    {
        j=Edge[i][e];
        if (DFN[j]==-)
        {
            Tarjan(j);
            Low[i]=min(Low[i],Low[j]);
        }
        else if (InStack[j])
            Low[i]=min(Low[i],DFN[j]);
    }
    if (DFN[i]==Low[i])
    {
        cout<<"TT    "<<i<<"   "<<Low[i]<<endl;
        ComponetNumber++;
        do
        {
            j=STACK[top--];
            InStack[j]=false;
            Component[ComponetNumber].push_back(j);
        }
        while (j!=i);
    }
}

void solve(int N)     //此图中点的个数，注意是0-indexed！
{
    memset(STACK,-,sizeof(STACK));
    memset(InStack,,sizeof(InStack));
    memset(DFN,-,sizeof(DFN));
    memset(Low,-,sizeof(Low));
    for(int i=;i<N;i++)
        if(DFN[i]==-)
            Tarjan(i);
}
/*
此算法正常工作的基础是图是0-indexed的。
*/
int main()
{
    Edge[].push_back();Edge[].push_back();
    Edge[].push_back();
    Edge[].push_back();Edge[].push_back();
    Edge[].push_back();Edge[].push_back();
    Edge[].push_back();
    int  N=;
    solve(N);
    cout<<"ComponetNumber is "<<ComponetNumber<<endl;
    for(int i=;i<N;i++)
        cout<<Low[i]<<" ";
    cout<<endl;
    for(int i=;i<N;i++)
    {
        for(int j=;j<Component[i].size();j++)
            cout<<Component[i][j];
        cout<<endl;
    }
    return ;
}

这个程序的运行过程和上图中表述的有些不同，他是先遍历到了1 2 4 6  3 5

Reference ： 以上基本上是全文摘抄自

http://www.byvoid.com/blog/scc-tarjan/

http://www.notonlysuccess.com/?p=181

两篇总结都不错。。这里只是做一个回顾。。

转载来自：http://www.cppblog.com/sosi/archive/2010/09/26/127797.aspx