利用Python检验你的策略参数是否过拟合(转)

过拟合现象

一般来说，量化研究员在优化其交易策略参数时难免会面临这样一个问题：优化过后的策略在样本内表现一般来说均会超过其在样本外的表现，即参数过拟合。
对于参数优化来说，由于优化时存在噪音，过拟合是不可避免的现象。然而为了追求策略的稳定性，我们应当尽可能地使过拟合风险最小化。
    为了检测在一个策略的参数优化过程中的过拟合风险，David H. Bailey等人在2015年发表了一篇名为《THE PROBABILITY OF BACKTEST OVERFITTING》的文章，
给出了一种估计参数过拟合概率的方法，本文将对此方法作较为详细的阐述。

主要思路

David H. Bailey等人的主要思路是这样的：对于一个策略的参数优化过程来说，我们能够获得一系列的样本内以及样本外的策略收益率序列，
并能够使用它们计算出策略的评价指标，如夏普比率，收益回撤比等等。是故，他们定义了这样一个概率空间（T，F，P） ，其中T为样本内指标与样本外指标的组合组成的集合，
如（样本内夏普比，相应的样本外夏普比）。在这样一个概率空间内，我们可以认为当我们选择最优的样本内参数时，我们得到的样本外策略表现劣于平均样本外策略表现的概率，即为参数过拟合的概率。

主要框架

    为了计量过拟合的概率，David H. Bailey等人使用了一种类似交叉验证的方法来对一个经过参数优化的策略回报矩阵重采样。
第一步

    我们在其参数空间上随机采样，得到N组不同的参数以及它们所对应的收益率序列，将其拼接成一个大矩阵M，其形状为TxN，T即是策略的回测时长。
第二步

    我们将矩阵M以一定的步长L按行分割为S个不同的区块，如从第1行到第L行为第一个区块，第L+1行到第2L行为第二个区块等。
第三步

    我们对这些不同的小矩阵随机分为两组，一组代表随机抽样产生的样本内组，另一组便是样本外组。我们将这些分块矩阵重新按照时间顺序拼接起来，得到了抽样的样本内收益率序列以及相应的抽样的样本外收益率序列。

第四步

    我们计算重新抽样后N个不同参数的策略的样本内收益率序列评价指标（如夏普比率），以及相应的N个样本外收益率序列评价指标。计算完成后，我们需要观察样本内最优策略对应的样本外策略的表现。在这里，我们使用Rank以及Relative Rank = Rank / (N + 1)来评价样本外策略的表现。此外，我们还使用Logit = Log(Relative Rank / (1 - Relative Rank))作为样本外策略表现的评价指标，注意到它是关于Relative Rank的增函数，是故样本外策略表现越好，其评价值便越大。此外，我们也能够获得样本内的最优夏普比率以及样本外相应的夏普比率。

第五步

    我们需要估计第四步中Logit统计量的分布，是故我们需要对第三步~第四步进行重复操作，操作的次数由我们自己决定，次数越多，其估计所得分布越稳健。

代码实现

    本文使用Python3 + WinPython初步实现了该方法，其所用到的包主要为numpy。此外，对于结果的可视化展示以及进一步分析还使用了pandas，matplotlib，seaborn以及sklearn。

    首先，实现该方法的代码如下：

# Overfitting Test
def PBOTest(rets,SampleTimes,block_len): 

'''
Probability of Overfitting Test Based On Return Matrix and Sharpe Ratio Inputs:
rets: Return Matrix with shape of TxN indicating N backtesting result using different params
SampleTimes: Overfitting Indicator Sample
Size block_len: Bootstrap Block Length Outputs:
PBO: Probability of Overffiting
POS: Probability of Getting Loss OutOfSample
rd: Overfitting Indicator Logit
ratios: Sharpe Ratios of Optimal InSample and of respective OutOfSample
''' 

# Compute Through the Framework
    N = rets.shape[1]
    S = len(rets)//block_len
    M = rets[:(block_len*S)]
    Ms = M.reshape((S,block_len,N))
    training_part_block = S//2 + S%2
    rd = np.zeros(SampleTimes)
    ratios = np.zeros((SampleTimes,2))
    for i in range(SampleTimes):
        rnd_num = np.random.rand(S).argsort()
        TPartOrder = np.sort(rnd_num[:training_part_block])
        VPartOrder = np.sort(rnd_num[training_part_block:])
        TJ = Ms[TPartOrder].reshape((training_part_block*block_len,N))
        VJ = Ms[VPartOrder].reshape(((S-training_part_block)*block_len,N))
        TSharpe = np.mean(TJ,axis = 0)/np.std(TJ,axis = 0)
        VSharpe = np.mean(VJ,axis = 0)/np.std(VJ,axis = 0)
        Vrelative_rank = (1 + VSharpe.argsort().argsort())/(N + 1)
        # Compute rd
        T_n_best = np.argmax(TSharpe)
        VT_n_best_rank = Vrelative_rank[T_n_best]
        logit = np.log(VT_n_best_rank/(1-VT_n_best_rank))
        rd[i] = logit
        # Compute Ratio
        ratios[i,0] = TSharpe[T_n_best]
        ratios[i,1] = VSharpe[T_n_best]
    PBO = np.sum(rd<=0) / SampleTimes
    POS = np.sum(ratios[:,1] <= 0) / SampleTimes
return PBO,POS,rd,ratios

我们来进一步分析一下这段代码：

    N = rets.shape[1]
    S = len(rets)//block_len
    M = rets[:(block_len*S)]
    Ms = M.reshape((S,block_len,N))
    training_part_block = S//2 + S%2
    rd = np.zeros(SampleTimes)
    ratios = np.zeros((SampleTimes,2)) 

这一段代码定义了回测中我们从参数空间抽取参数进行回测的次数N，以及区块的长度block_len和区块的个数S，并且如果rets的行不能整除S，我们便舍去除不尽的部分，最后得到的矩阵为M。Ms为一个三维矩阵，是经过分块的矩阵的组合。training_part_block是我们在第三步中需要抽取的小矩阵的个数。rd，ratios分别是最终结果统计量Logit以及夏普比率的预分配空间。

        rnd_num = np.random.rand(S).argsort()
        TPartOrder = np.sort(rnd_num[:training_part_block])
        VPartOrder = np.sort(rnd_num[training_part_block:])
        TJ = Ms[TPartOrder].reshape((training_part_block*block_len,N))
        VJ = Ms[VPartOrder].reshape(((S-training_part_block)*block_len,N))     

这一段代码主要实现了框架中的第三步以及第四步，如重新采样等。首先我们生成一串长度为S的随机数，利用argsort函数得到其下标的排序rnd_num。其次，我们利用前training_part_block个下标作为组成样本内矩阵的下标TPartOrder，并且重新拼接形成TJ。VPartOrder以及VJ同理。

        TSharpe = np.mean(TJ,axis = 0)/np.std(TJ,axis = 0)
        VSharpe = np.mean(VJ,axis = 0)/np.std(VJ,axis = 0)
        Vrelative_rank = (1 + VSharpe.argsort().argsort())/(N + 1)     

然后，我们计算样本内所有策略的夏普比率TSharpe以及样本外所有策略的夏普比率VSharpe，并且计算得到代表样本外策略表现的Relative Rank的Vrelative_rank。

        # Compute rd
        T_n_best = np.argmax(TSharpe)
        VT_n_best_rank = Vrelative_rank[T_n_best]
        logit = np.log(VT_n_best_rank/(1-VT_n_best_rank))
        rd[i] = logit
        # Compute Ratio
        ratios[i,0] = TSharpe[T_n_best]
        ratios[i,1] = VSharpe[T_n_best]     

接下来，我们能够计算得到最优样本内策略对应的样本外Realative Rank以及Logit统计量，并且将其赋值给预先分配好的空间。

    PBO = np.sum(rd<=0) / SampleTimes
    POS = np.sum(ratios[:,1] <= 0) / SampleTimes 

最后，我们计算出过拟合的概率PBO，即为Logit统计量小于0的概率。POS为样本外策略夏普比率为负的概率，即优化出亏损策略的概率。

框架测试

    那最后让我们来尝试一下这一个框架吧。我们首先下载得到上证指数从2010年1月1日到2017年5月16日之间的日行情，利用pandas进行读入。我们使用简单的均线策略进行测试：如快线上穿慢线即做多，快线下穿慢线做空。其参数为快线的计算长度以及慢线的计算长度。暂时不设止损线。策略的代码如下：

def MA(close,num = 5):
    res = [close[0]*1]
    for i in range(1,len(close)):
        if i >= num:
            res.append((res[-1]*num - close[i-num] + close[i])/num)
        else:
            res.append((res[-1]*i + close[i])/(i+1))
        res = np.array(res)
        return res

def backtest(data,params = [],num = 100,money = 1e6):
    Fastlen,Slowlen,thdAB,stoploss = params
    high = data['high'].values
    low = data['low'].values
    close = data['close'].values
    hlen = len(close)
    profit = np.zeros(hlen)
    Ama = MA(close, Fastlen)
    Bma = MA(close, Slowlen)
    opened = False
    long = False
    opened_price = 0
    for i in range(hlen):
        if not opened:
            if Ama[i]/Bma[i] - 1 > thdAB:
                opened = True
                long = True
                opened_price = close[i]
                profit[i] = -close[i]*0.0002*num
            elif Ama[i]/Bma[i] - 1 < -thdAB:
                opened = True
                long = False
                opened_price = close[i]
                profit[i] = -close[i]*0.0012*num
        else:
            if long:
                profit[i] = (close[i] - close[i-1])*num
                if Ama[i] < Bma[i] or low[i]/opened_price - 1 < -stoploss:
                    opened = False
                    profit[i] = profit[i] - close[i]*num*0.0012
            else:
                profit[i] = (close[i-1] - close[i])*num
                if Ama[i] > Bma[i] or high[i]/opened_price - 1 > stoploss:
                    opened = False
                    profit[i] = profit[i] - close[i]*num*0.0002
    rets = profit / money
    equity = np.cumprod(1 + rets)
    return rets,equity

利用回测函数，我们能够得到相应的收益率序列以及净值曲线。

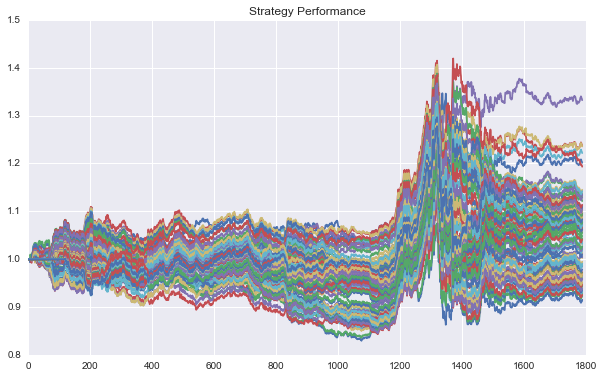
我们对该策略进行参数的重采样，有：

    X = np.arange(5,120)
    rets = np.array([backtest(data,[x,2*x,0,1],100)[0] for x in X]).T

便能够得到我们需要的收益率序列矩阵，对其进行策略参数过拟合测试：

np.random.seed(0)
PBO,POS,rd,ratios = PBOTest(rets,SampleTimes = 1000,block_len = 50)

我们得到了其过拟合的概率以及亏损的概率。在该例子中，他们分别为70.2%以及 56.3%。此外，我们可以对结果进行进一步的分析：

    np.random.seed(0)
    PBO,POS,rd,ratios = PBOTest(rets,SampleTimes = 1000,block_len = 50)

    # Histgram of Dist of logit
    plt.figure(figsize = (10,6))
    plt.title('Distribution of Logit')
    plt.hist(rd,bins = 20) 

    # Performance Degration
    model = sl.LinearRegression()
    model.fit(ratios[:,0].reshape((-1,1)),ratios[:,1])
    plt.figure(figsize = (10,8))
    plt.title('Performance Degration')
    plt.plot(ratios[:,0],ratios[:,1],'.')
    plt.plot(ratios[:,0],model.decision_function(ratios[:,0].reshape((-1,1))),'-')
    plt.xlabel('IS Sharpe Ratio')
    plt.ylabel('OOS Sharpe Ratio')

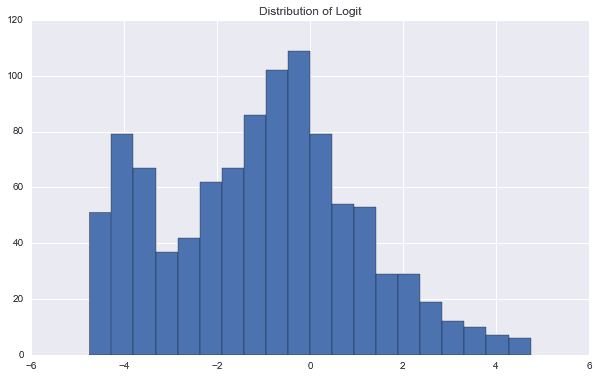
该图显示了Logit统计量的分布。

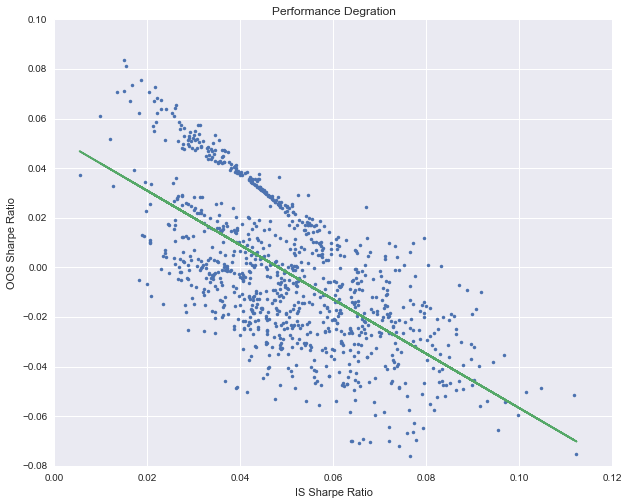
该图形象地显示出了随着样本内夏普比率的上升，样本外的夏普比率的变化趋势。

总结

    本文实现了David H. Bailey等人的方法对策略过拟合的概率进行了测试。该方法有一个特点，那便是我们仅仅需要回测收益率序列便能够对其是否过拟合进行测试，其测试的本质实质上是看样本内以及样本外策略的盈利能力的延续性，以及优化过程中是否所有的时间段的策略表现都会随着参数的变化而同时被优化。利用该方法，我们通过估计过拟合的概率，能够在一定程度上评估策略的稳健性。

作者：时风_瞬
链接：http://www.jianshu.com/p/3bd86cca96bd

THE PROBABILITY OF BACKTEST OVERFITTING    https://files.cnblogs.com/files/hdu-2010/THE_PROBABILITY_OF_BACKTEST_OVERFITTING.pdf