BZOJ 3771 生成函数，FFT

Description

我们讲一个悲伤的故事。

从前有一个贫穷的樵夫在河边砍柴。

这时候河里出现了一个水神，夺过了他的斧头，说：

“这把斧头，是不是你的？”

樵夫一看：“是啊是啊！”

水神把斧头扔在一边，又拿起一个东西问：

“这把斧头，是不是你的？”

樵夫看不清楚，但又怕真的是自己的斧头，只好又答：“是啊是啊！”

水神又把手上的东西扔在一边，拿起第三个东西问：

“这把斧头，是不是你的？”

樵夫还是看不清楚，但是他觉得再这样下去他就没法砍柴了。

于是他又一次答：“是啊是啊！真的是！”

水神看着他，哈哈大笑道：

“你看看你现在的样子，真是丑陋！”

之后就消失了。

樵夫觉得很坑爹，他今天不仅没有砍到柴，还丢了一把斧头给那个水神。

于是他准备回家换一把斧头。

回家之后他才发现真正坑爹的事情才刚开始。

水神拿着的的确是他的斧头。

但是不一定是他拿出去的那把，还有可能是水神不知道怎么偷偷从他家里拿走的。

换句话说，水神可能拿走了他的一把，两把或者三把斧头。

樵夫觉得今天真是倒霉透了，但不管怎么样日子还得过。

他想统计他的损失。

樵夫的每一把斧头都有一个价值，不同斧头的价值不同。总损失就是丢掉的斧头价值和。

他想对于每个可能的总损失，计算有几种可能的方案。

注意：如果水神拿走了两把斧头a和b，(a,b)和(b,a)视为一种方案。拿走三把斧头时，(a,b,c),(b,c,a),(c,a,b),(c,b,a),(b,a,c),(a,c,b)视为一种方案。

Input

第一行是整数N，表示有N把斧头。

接下来n行升序输入N个数字Ai，表示每把斧头的价值。

Output

若干行，按升序对于所有可能的总损失输出一行x y，x为损失值，y为方案数。

Sample Input

4
4
5
6
7

Sample Output

4 1
5 1
6 1
7 1
9 1
10 1
11 2
12 1
13 1
15 1
16 1
17 1
18 1
样例解释
11有两种方案是4+7和5+6，其他损失值都有唯一方案，例如4=4,5=5,10=4+6,18=5+6+7.

HINT

所有数据满足：Ai<=40000

题意：

给出 n个物品，价值为别为Xi且各不相同，现在可以取1个、2个或3个，问每种价值和有几种情况？顺序不同算一种。

解法：

显然是个母函数，A表示每种物品取一个的情况，B表示每种物品取二个的情况，C表示每种物品取三个的情况。用指数表示价值，系数表示该价值的个数，显然多项式相乘后指数会相加，系数会相乘，很容易就求出来了。

所以对于每种物品价值x,A[x]++,B[2*x]++,C[3*x]++。

如果取1个物品，答案就是A。

如果取2个物品，A^2中有重复的(x,x)的情况，所以答案为A^2-B。

如果去3个物品，A^3中可能有(x,x,x)(x,x,y)(x,y,x)(y,x,x)这几种重复的情况，而A*B能够求出所有形容(x,x,x)和(x,y,y)的情况数。(x,x,y)(x,y,x)(y,x,x)总的情况数=(x,y,y)*3，而A*B*3又会多减去了两次(x,x,x)，所以要用C加回来。所以答案为A^3-3*B*A+2C。又由于顺序不同算一种情况，因为每种物品价值都不一样，情况(2)/2,情况(3)/6。

故总情况数量等于：

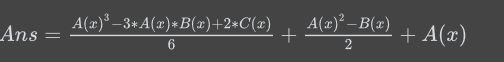
#include <bits/stdc++.h>
using namespace std;
const int maxn = 300000;
typedef long long LL;
const double PI = acos(-1.0);
typedef complex <double> Complex;

void rader(Complex *y, int len) {
    for(int i = 1, j = len / 2; i < len - 1; i++) {
        if(i < j) swap(y[i], y[j]);
        int k = len / 2;
        while(j >= k) {j -= k; k /= 2;}
        if(j < k) j += k;
    }
}
void fft(Complex *y, int len, int op) {
    rader(y, len);
    for(int h = 2; h <= len; h <<= 1) {
        double ang = op * 2 * PI / h;
        Complex wn(cos(ang), sin(ang));
        for(int j = 0; j < len; j += h) {
            Complex w(1, 0);
            for(int k = j; k < j + h / 2; k++) {
                Complex u = y[k];
                Complex t = w * y[k + h / 2];
                y[k] = u + t;
                y[k + h / 2] = u - t;
                w = w * wn;
            }
        }
    }
    if(op == -1) for(int i = 0; i < len; i++) y[i] /= len;
}

Complex a[maxn],b[maxn],c[maxn];
int n, len, x, m, mx;

int main()
{
    scanf("%d", &n);
    for(int i=0; i<n; i++){
        scanf("%d", &x);
        a[x]+=(1),b[2*x]+=(1),c[3*x]+=(1);
        mx = max(mx, 3*x);
    }
    mx++;
    len = 1;
    while(len < mx*2){
        len <<= 1;
    }
    m = len+1;
    fft(a, len, 1);
    fft(b, len, 1);
    fft(c, len, 1);
    Complex t2=(2),t3=(3),t6=(6);
    for (int i=0;i<len;i++)
        a[i]=(a[i]*a[i]*a[i]-t3*a[i]*b[i]+t2*c[i])/t6+(a[i]*a[i]-b[i])/t2+a[i];
    fft(a, len, -1);
    for(int i=1; i<m; i++){
        LL num = (LL)(a[i].real()+0.5);
        if(num!=0) printf("%d %lld\n", i,num);
    }
    return 0;
}