[TCO2013]Block3Checkers

题意：一个网格上有一些障碍和$3$个在网格边界上的棋子，你要添加一些障碍使得没有两个棋子四连通，问最少添加多少个障碍

官方题解——一张图教你做人...

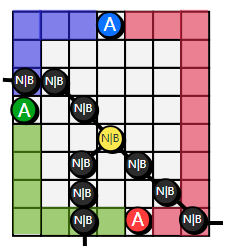
三个棋子将网格边界分成三段，添加障碍后网格中一定存在一个点使得它可以到这三段（只走障碍的路径，八连通）

所以找出这三段后分别以它们为起点跑最短路即可，经过障碍权值为$0$，经过空地权值为$1$

#include<stdio.h>
#include<queue>
#include<string.h>
#include<vector>
#include<string>
using namespace std;
int h[410],nex[7010],to[7010],v[7010],M;
void add(int a,int b,int c){
	M++;
	to[M]=b;
	v[M]=c;
	nex[M]=h[a];
	h[a]=M;
}
int dis[410];
struct pr{
	int x,d;
	pr(int u=0){x=u;d=dis[u];}
}t;
bool operator<(pr a,pr b){return a.d>b.d;}
priority_queue<pr>q;
void dijk(int x){
	int i;
	memset(dis,63,sizeof(dis));
	dis[x]=0;
	q.push(x);
	while(!q.empty()){
		t=q.top();
		q.pop();
		x=t.x;
		if(t.d!=dis[x])continue;
		for(i=h[x];i;i=nex[i]){
			if(dis[x]+v[i]<dis[to[i]]){
				dis[to[i]]=dis[x]+v[i];
				q.push(to[i]);
			}
		}
	}
}
const int g4[4][2]={{0,1},{0,-1},{1,0},{-1,0}},g8[8][2]={{-1,-1},{-1,0},{-1,1},{0,-1},{0,1},{1,-1},{1,0},{1,1}};
int d[3][410],n,m;
vector<string>mp;
bool ok(int x,int y){
	return 0<=x&&x<n&&0<=y&&y<m;
}
bool edge(int x,int y){
	return ok(x,y)&&(x==0||x==n-1||y==0||y==m-1);
}
void dfs(int fx,int fy,int x,int y,int s){
	int i,tx,ty;
	if(mp[x][y]=='A')return;
	add(s,x*m+y+1,0);
	add(x*m+y+1,s,mp[x][y]=='.');
	for(i=0;i<4;i++){
		tx=x+g4[i][0];
		ty=y+g4[i][1];
		if((tx!=fx||ty!=fy)&&edge(tx,ty))dfs(x,y,tx,ty,s);
	}
}
class Block3Checkers{
	public:
		int blockThem(vector<string>mp){
			int i,j,k,x,y,f,s[3],ans;
			::mp=mp;
			n=mp.size();
			m=mp[0].length();
			s[0]=n*m+1;
			s[1]=n*m+2;
			s[2]=n*m+3;
			f=0;
			for(i=0;i<m;i++){
				if(mp[0][i]=='A'){
					if((i&&mp[0][i-1]=='A')||(i<m-1&&mp[0][i+1]=='A')||mp[1][i]=='A')return 100;
					if(i==0)
						dfs(0,0,1,0,s[f]);
					else
						dfs(0,i,0,i-1,s[f]);
					f++;
				}
				if(mp[n-1][i]=='A'){
					if((i&&mp[n-1][i-1]=='A')||(i<m-1&&mp[n-1][i+1]=='A')||mp[n-2][i]=='A')return 100;
					if(i==m-1)
						dfs(n-1,m-1,n-2,m-1,s[f]);
					else
						dfs(n-1,i,n-1,i+1,s[f]);
					f++;
				}
			}
			for(i=1;i<n-1;i++){
				if(mp[i][0]=='A'){
					if(mp[i-1][0]=='A'||mp[i+1][0]=='A')return 100;
					dfs(i,0,i+1,0,s[f]);
					f++;
				}
				if(mp[i][m-1]=='A'){
					if(mp[i-1][m-1]=='A'||mp[i+1][m-1]=='A')return 100;
					dfs(i,m-1,i-1,m-1,s[f]);
					f++;
				}
			}
			for(i=0;i<n;i++){
				for(j=0;j<m;j++){
					if(mp[i][j]!='A'){
						for(k=0;k<8;k++){
							x=i+g8[k][0];
							y=j+g8[k][1];
							if(ok(x,y)&&mp[x][y]!='A')add(i*m+j+1,x*m+y+1,mp[i][j]=='.');
						}
					}
				}
			}
			for(i=0;i<3;i++){
				dijk(s[i]);
				memcpy(d[i],dis,sizeof(dis));
			}
			ans=n*m;
			for(i=0;i<n;i++){
				for(j=0;j<m;j++){
					if(mp[i][j]!='A'){
						x=i*m+j+1;
						ans=min(ans,d[0][x]+d[1][x]+d[2][x]+(mp[i][j]=='.'));
					}
				}
			}
			return ans;
		}
};
/*
int main(){
	vector<string>vt;
	char s[30];
	Block3Checkers cl;
	while(~scanf("%s",s))vt.push_back(s);
	printf("%d",cl.blockThem(vt));
}
*/