kosaraju求强连通分量

在了解kosaraju算法之前我们先了解一下什么是强连通分量，在有向图中如果两个定点vi,ui存在一条路劲从vi到达ui且也存在一条路劲从ui到达vi那么由ui和vi这两个点构成的图成为强连通图,简洁一点就是存在两个或两个点以它们之间可以相互可达由这些点构成的图就称之为强连通图它们的存在形式可以如下

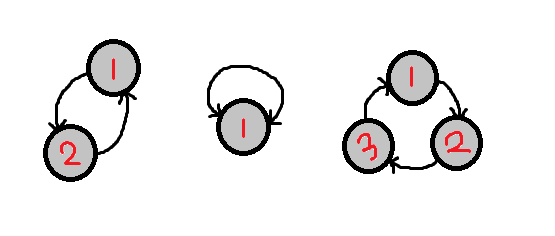
当然一个点也是一个强连通分量，它们都满足所有点之间都可以互相可达。

以上就是对强连通分量的介绍接下来对kosaraju算法思路进行分析。

我们将对下面这个图进行对kosaraju算法进行解析：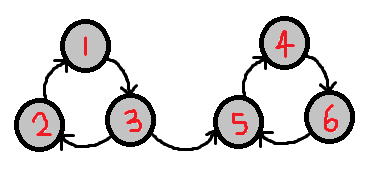

我们可以发现此图存在两个强联通分量它们分别是，强连通分量A：1，3，2； 强连通分量B：5，4，6。

kosaraju的主要思想就是图进行两边dfs但是第二遍dfs的图必须是与原图相反的图，然后将第一遍的dfs比例的顺序用栈存起来然后再用栈内的元素对原图的反向图进行遍历最后就可以求得强连通分量。

Q：为什么要跑两边dfs?

A：kosaraju主要还是介于dfs遍历原理上，对于上图的dfs遍历我们假设以点1作为起点所以我们可以的的dfs遍历序为下图中绿色的回溯的点push进入栈中

所以栈内的值为1，3，5，4，6，2。

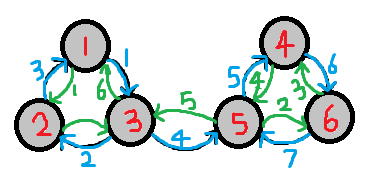
当以点1为起点进行dfs搜索我们会从点1搜到点6并不能确定强连通分量的元素但是当我们将原图反向建图再跑dfs的时候我们会发现每个强连通分量都可以分开了

为什么？我们将用图解释：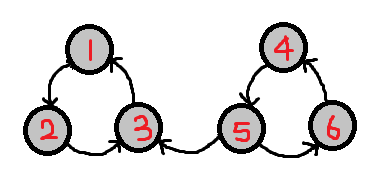

原图反图的建立，我们可以发下当我们把原图反向建立时，我们可以发现由3-->5这条边变成了5-->3这条边，当我们再以点1为起点进行dfs时我们可以发现与之前不同点1不能遍历完全部节点

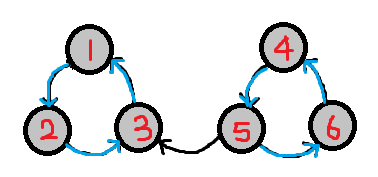
因此第二遍dfs跑原图的反图时我们就将两个强连通分量给分开了，正好在第一遍dfs我们就将正图的dfs序存入栈中，那我们在第二遍dfs的时候我们只需要将栈中的元素取出跑一边反向图即可

求得强连通分量。

上面这个图我们可以手推得到，强连通分量1：  1，3，2；   强连通分量2：  5，4，6。

代码：
第一遍dfs跑正图将图的dfs序存入栈中：

void dfs1(int x)
{
    if(vis[x]) return;
    vis[x]=true;
    for(int i=;i<vt[x].size();i++)
        dfs1(vt[x][i]);
    z.push(x);
    return;
}

第二遍dfs跑一边反着的原图：

void dfs2(int x)
{
    for(int i=;i<rvt[x].size();i++)
    {
        if(vis[rvt[x][i]]) continue;
        vis[rvt[x][i]]=true;
        dfs2(rvt[x][i]);
        out<<rvt[x][i]<<" ";
    }
    return;
}
void scc_find()
{
    memset(vis,false,sizeof(vis));//跑第二遍dfs的时候vis标记数组一定要初始化为false
    while(!z.empty())//对栈内的元素进行dfs寻找强连通分量
    {
        int t=z.top();
        z.pop();
        if(vis[t]) continue;
        vis[t]=true;
        scc++;
        out<<"group:"<<t<<" ";
        dfs2(t);
        out<<endl;
    }
    return;
}

完整代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <iomanip>
#include <stack>
#include <vector>
using namespace std;
#define in cin
#define out cout
typedef long long insert;
const int N=2e5+;
stack<int> z;
vector<int> vt[N];
vector<int> rvt[N];
insert n,m,x,y,scc;
bool vis[N];
void inital_value()
{
    for(int i=;i<=m;i++)
    {
        in>>x>>y;
        vt[x].push_back(y);
        rvt[y].push_back(x);//反向存图
    }
    return;
}
void dfs1(int x)
{
    if(vis[x]) return;
    vis[x]=true;
    for(int i=;i<vt[x].size();i++)
        dfs1(vt[x][i]);
    z.push(x);
    return;
}
void dfs2(int x)
{
    for(int i=;i<rvt[x].size();i++)
    {
        if(vis[rvt[x][i]]) continue;
        vis[rvt[x][i]]=true;
        dfs2(rvt[x][i]);
        out<<rvt[x][i]<<" ";
    }
    return;
}
void scc_find()
{
    memset(vis,false,sizeof(vis));//跑第二遍dfs的时候vis标记数组一定要初始化为false
    while(!z.empty())//对栈内的元素进行dfs寻找强连通分量
    {
        int t=z.top();
        z.pop();
        if(vis[t]) continue;
        vis[t]=true;
        scc++;
        out<<"group:"<<t<<" ";
        dfs2(t);
        out<<endl;
    }
    return;
}
int main()
{
    in>>n>>m;
    inital_value();
    for(int i=;i<=n;i++)
    {
        if(vis[i]) continue;
        dfs1(i);
    }
    scc_find();
    out<<"强连通分量总数"<<endl;
    out<<scc<<endl;
    return ;
}