poj 1692(动态规划)

Crossed Matchings

Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 2711		Accepted: 1759

Description

There are two rows of positive integer numbers. We can draw one line segment between any two equal numbers, with values r, if one of them is located in the first row and the other one is located in the second row. We call this line segment an r-matching segment. The following figure shows a 3-matching and a 2-matching segment.


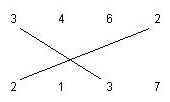
We want to find the maximum number of matching segments possible to draw for the given input, such that:

1. Each a-matching segment should cross exactly one b-matching segment, where a != b .

2. No two matching segments can be drawn from a number. For example, the following matchings are not allowed.



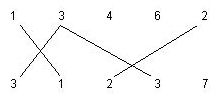
Write a program to compute the maximum number of matching segments for the input data. Note that this number is always even.

Input

The
first line of the input is the number M, which is the number of test
cases (1 <= M <= 10). Each test case has three lines. The first
line contains N1 and N2, the number of integers on the first and the
second row respectively. The next line contains N1 integers which are
the numbers on the first row. The third line contains N2 integers which
are the numbers on the second row. All numbers are positive integers
less than 100.

Output

Output
should have one separate line for each test case. The maximum number of
matching segments for each test case should be written in one separate
line.

Sample Input

3
6 6
1 3 1 3 1 3
3 1 3 1 3 1
4 4
1 1 3 3
1 1 3 3
12 11
1 2 3 3 2 4 1 5 1 3 5 10
3 1 2 3 2 4 12 1 5 5 3

Sample Output

6
0
8

Source

Tehran 1999

 

这题借鉴了别人的想法。http://blog.csdn.net/gubojun123/article/details/8447071

开始觉得是二分图匹配，然后现在刚弄到动归。。二分图也忘了，被题意吓唬住了。还是要多加练习啊。。有点区间DP的意思吧。。

#include <stdio.h>
#include <iostream>
#include <string.h>
using namespace std;
const int N = ;

int dp[N][N];  ///dp[i][j]表示第1行前i个字符和第二行前j个字符的最大匹配
int main()
{
    int tcase;
    int a[N],b[N];
    scanf("%d",&tcase);
    while(tcase--){
        int n1,n2;
        scanf("%d%d",&n1,&n2);
        for(int i=;i<=n1;i++) {
            scanf("%d",&a[i]);
        }
        for(int i=;i<=n2;i++){
            scanf("%d",&b[i]);
        }
        memset(dp,,sizeof(dp));
        for(int i=;i<=n1;i++){
            for(int j=;j<=n2;j++){
               dp[i][j] = max(dp[i-][j],dp[i][j-]);
               if(a[i]!=b[j]){
                    int k1,k2;
                    for(k1 = i-;k1>;k1--){
                        if(a[k1]==b[j]) break;
                    }
                    for(k2=j-;k2>;k2--){
                        if(b[k2]==a[i]) break;
                    }
                    if(k1!=&&k2!=){
                        dp[i][j] = max(dp[i][j],dp[k1-][k2-]+); ///在 dp[k1-1][k2-1]之后又产生了两组新的匹配
                    }
               }
            }
        }
        printf("%d\n",dp[n1][n2]);
    }
    return ;
}