洛谷 P4175 [CTSC2008]网络管理 解题报告

P4175 [CTSC2008]网络管理

题目描述

带修改树上链的第\(k\)大

输入输出格式

输入格式：

第一行为两个整数\(N\)和\(Q\)，分别表示路由器总数和询问的总数。

第二行有\(N\)个整数，第\(i\)个数表示编号为\(i\)的路由器初始的数据延迟时间\(T_i\)。

紧接着\(N-1\)行，每行包含两个整数\(x\)和\(y\)。表示有一条光缆连接路由器\(x\)和路由器\(y\)。

紧接着是\(Q\)行，每行三个整数\(k\)、\(a\)、\(b\)。

如果\(k=0\)，则表示路由器\(a\)的状态发生了变化，它的数据交换延迟时间由\(T_a\)变为\(b\)。

如果\(k>0\)，则表示询问\(a\)到\(b\)的路径上所经过的所有路由器（包括\(a\)和\(b\)）中延迟第\(k\)大的路由器的延迟时间。注意\(a\)可以等于\(b\)，此时路径上只有一个路由器。

输出格式：

对于每一个第二种询问（\(k>0\)），输出一行。包含一个整数为相应的延迟时间。如果路径上的路由器不足\(k\)个，则输出信息“\(\tt{invalid request!}\)”（全部小写不包含引号，两个单词之间有一个空格）。

说明

测试数据满足\(N,Q\le 80000\),任意一个路由器在任何时刻都满足延迟时间小于\(10^8\)。

对于所有询问满足\(0\le K\le N\) 。

---

写了两种分别是\(O((N+Q)\log^2N\log10^8)\)和\(O((N+Q)\log N\log10^8)\)的

谁知道前面的跑得快一些...

---

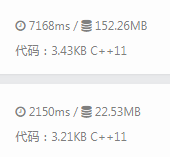
三个\(\log\)的思路是 整体二分+树链剖分+树状数组

其实就是在普通的整体二分的基础上加了个树链剖分用来维护链。

思路比较简单。

Code:

#include <cstdio>
#include <cctype>
const int N=240010;
int head[N],to[N],Next[N],cnt;
void add(int u,int v)
{
    to[++cnt]=v,Next[cnt]=head[u],head[u]=cnt;
}
struct node{int op,x,y,k;}q[N],ql[N],qr[N];
int n,m,Q,qu,ans[N],poi[N];
int read()
{
    int x=0;char c=getchar();
    while(!isdigit(c)) c=getchar();
    while(isdigit(c)){x=x*10+c-'0';c=getchar();}
    return x;
}
int dfn[N],top[N],f[N],dep[N],ws[N],siz[N],dfsclock;
void dfs1(int now)
{
    siz[now]=1;
    for(int i=head[now];i;i=Next[i])
    {
        int v=to[i];
        if(v==f[now]) continue;
        f[v]=now;
        dep[v]=dep[now]+1;
        dfs1(v);
        siz[now]+=siz[v];
        if(siz[ws[now]]<siz[v]) ws[now]=v;
    }
}
void dfs2(int now,int anc)
{
    dfn[now]=++dfsclock;
    top[now]=anc;
    if(ws[now]) dfs2(ws[now],anc);
    for(int i=head[now];i;i=Next[i])
        if(!dfn[to[i]])
            dfs2(to[i],to[i]);
}
int LCA(int x,int y)
{
    while(top[x]!=top[y])
    {
        if(dep[top[x]]>=dep[top[y]])
            x=f[top[x]];
        else
            y=f[top[y]];
    }
    return dep[x]<dep[y]?x:y;
}
int S[N],tmp;
void Swap(int &x,int &y){tmp=x,x=y,y=tmp;}
void change(int x,int d){while(x<=n)S[x]+=d,x+=x&-x;}
int ask(int x){int sum=0;while(x)sum+=S[x],x-=x&-x;return sum;}
int query(int x,int y)
{
    int sum=0;
    while(top[x]!=top[y])
    {
        if(dep[top[x]]>=dep[top[y]])
        {
            sum+=ask(dfn[x])-ask(dfn[top[x]]-1);
            x=f[top[x]];
        }
        else
        {
            sum+=ask(dfn[y])-ask(dfn[top[y]]-1);
            y=f[top[y]];
        }
    }
    if(dep[x]<dep[y]) Swap(x,y);
    sum+=ask(dfn[x])-ask(dfn[y]-1);
    return sum;
}
#define rep(i,a,b) for(int i=a;i<=b;i++)
void divide(int l,int r,int s,int t)
{
    if(s>t)return;
    if(l==r){rep(i,s,t)ans[q[i].op]=l;return;}
    int mid=l+r>>1,lp=0,rp=0;
    rep(i,s,t)
    {
        if(q[i].op)
        {
            int c=query(q[i].x,q[i].y);
            if(q[i].k<=c) qr[++rp]=q[i];
            else ql[++lp]=q[i],ql[lp].k-=c;
        }
        else
        {
            if(q[i].x>mid) change(dfn[q[i].y],q[i].k),qr[++rp]=q[i];
            else ql[++lp]=q[i];
        }
    }
    rep(i,s,t) if(!q[i].op&&q[i].x>mid) change(dfn[q[i].y],-q[i].k);
    rep(i,s,s+lp-1) q[i]=ql[i+1-s];
    rep(i,s+lp,t) q[i]=qr[i+1-s-lp];
    divide(l,mid,s,s+lp-1),divide(mid+1,r,s+lp,t);
}
int main()
{
    m=n=read(),Q=read();
    rep(i,1,n) poi[i]=q[i].x=read(),q[i].y=i,q[i].k=1;
    int u,v;rep(i,1,(n-1)) u=read(),v=read(),add(u,v),add(v,u);
    dep[1]=1;
    dfs1(1),dfs2(1,1);
    rep(i,1,Q)
    {
        ++m;
        q[m].op=read();
        if(q[m].op)
        {
            q[m].x=read(),q[m].y=read(),q[m].k=q[m].op,q[m].op=++qu;
            int lca=LCA(q[m].x,q[m].y);
            if(dep[q[m].x]+dep[q[m].y]-dep[lca]-dep[f[lca]]<q[m].k) ans[qu]=-1,--m;
        }
        else
        {
            int p=read();
            q[m].x=poi[p],q[m].y=p,q[m].k=-1;
            ++m;
            poi[p]=q[m].x=read(),q[m].y=p,q[m].k=1;
        }
    }
    divide(0,(int)(1e8),1,m);
    rep(i,1,qu) if(~ans[i]) printf("%d\n",ans[i]);else puts("invalid request!");
    return 0;
}

---

两个\(\log\)的思路就是树状数组套权值线段树了。

对于查询一条\(u\)到根的链，我们可以理解为每个\(u\)到根的路径上的点都做了贡献，我们可以事先把贡献都放到\(u\)上，然后直接查询\(u\)就可以了。而一个点可以对也仅对\(\tt{Ta}\)每个子树的点产生一个贡献，这段子树在\(dfs\)序上是连续的。

在信息可加减的情况下，查询任意的链只需要两个端点的信息减去它们LCA初即LCA处父亲的信息即可。

考虑每个点维护一个权值线段树的话，是不容易维护区间信息的。不妨借助差分的思想，就可以转换成维护单点修改和区间查询了。

直接在权值线段树的外层套树状数组，然后每次查询时在树上二分即可。

Code:

#include <cstdio>
#include <cctype>
const int N=8e4+10;
const int inf=1e8;
int read()
{
    int x=0;char c=getchar();
    while(!isdigit(c)) c=getchar();
    while(isdigit(c)) {x=x*10+c-'0';c=getchar();}
    return x;
}
int n,Q,poi[N];
int head[N],to[N<<1],Next[N<<1],cnt;
void add(int u,int v)
{
    to[++cnt]=v,Next[cnt]=head[u],head[u]=cnt;
    to[++cnt]=u,Next[cnt]=head[v],head[v]=cnt;
}
int f[N][20],dep[N],low[N],dfn[N],dfsclock;
void dfs(int now)
{
    dfn[now]=++dfsclock;
    for(int i=1;f[now][i-1];i++) f[now][i]=f[f[now][i-1]][i-1];
    for(int i=head[now];i;i=Next[i])
    {
        int v=to[i];
        if(v==f[now][0]) continue;
        dep[v]=dep[now]+1;
        f[v][0]=now;
        dfs(v);
    }
    low[now]=dfsclock;
}
int LCA(int x,int y)
{
    if(dep[x]<dep[y]) return LCA(y,x);
    for(int i=18;~i;i--)
        if(dep[f[x][i]]>=dep[y])
            x=f[x][i];
    if(x==y) return x;
    for(int i=18;~i;i--)
        if(f[x][i]!=f[y][i])
            x=f[x][i],y=f[y][i];
    return f[x][0];
}
#define ls ch[now][0]
#define rs ch[now][1]
int ch[N*200][2],sum[N*200],tot,root[N];
void change(int &now,int l,int r,int p,int d)
{
    if(!now) now=++tot;
    if(l==r) {sum[now]+=d;return;}
    int mid=l+r>>1;
    if(p<=mid) change(ls,l,mid,p,d);
    else change(rs,mid+1,r,p,d);
    sum[now]=sum[ls]+sum[rs];
}
#define rep(i,a,b) for(int i=a;i<=b;i++)
void modify(int x,int loc,int d){while(x<=n)change(root[x],1,inf,loc,d),x+=x&-x;}
int sa[20],sb[20],sc[20],sd[20];
int query(int a,int b,int c,int d,int k)
{
    sa[0]=sb[0]=sc[0]=sd[0]=0;
    for(int i=a;i;i-=i&-i) sa[++sa[0]]=root[i];
    for(int i=b;i;i-=i&-i) sb[++sb[0]]=root[i];
    for(int i=c;i;i-=i&-i) sc[++sc[0]]=root[i];
    for(int i=d;i;i-=i&-i) sd[++sd[0]]=root[i];
    int l=1,r=inf;
    while(l<r)
    {
        int mid=l+r>>1,c=0;
        for(int i=1;i<=sa[0];i++) c+=sum[ch[sa[i]][1]];
        for(int i=1;i<=sb[0];i++) c+=sum[ch[sb[i]][1]];
        for(int i=1;i<=sc[0];i++) c-=sum[ch[sc[i]][1]];
        for(int i=1;i<=sd[0];i++) c-=sum[ch[sd[i]][1]];
        if(c>=k)
        {
            for(int i=1;i<=sa[0];i++) sa[i]=ch[sa[i]][1];
            for(int i=1;i<=sb[0];i++) sb[i]=ch[sb[i]][1];
            for(int i=1;i<=sc[0];i++) sc[i]=ch[sc[i]][1];
            for(int i=1;i<=sd[0];i++) sd[i]=ch[sd[i]][1];
            l=mid+1;
        }
        else
        {
            for(int i=1;i<=sa[0];i++) sa[i]=ch[sa[i]][0];
            for(int i=1;i<=sb[0];i++) sb[i]=ch[sb[i]][0];
            for(int i=1;i<=sc[0];i++) sc[i]=ch[sc[i]][0];
            for(int i=1;i<=sd[0];i++) sd[i]=ch[sd[i]][0];
            k-=c,r=mid;
        }
    }
    return l;
}
int main()
{
    n=read(),Q=read();
    rep(i,1,n) poi[i]=read();
    rep(i,1,(n-1)) add(read(),read());
    dep[1]=1;dfs(1);
    rep(i,1,n)
        modify(dfn[i],poi[i],1),modify(low[i]+1,poi[i],-1);
    rep(i,1,Q)
    {
        int op=read();
        if(op)
        {
            int u=read(),v=read();
            int lca=LCA(u,v);
            if(dep[u]+dep[v]-dep[lca]-dep[f[lca][0]]<op) puts("invalid request!");
            else printf("%d\n",query(dfn[u],dfn[v],dfn[lca],dfn[f[lca][0]],op));
        }
        else
        {
            int p=read();
            modify(dfn[p],poi[p],-1),modify(low[p]+1,poi[p],1);
            poi[p]=read();
            modify(dfn[p],poi[p],1),modify(low[p]+1,poi[p],-1);
        }
    }
    return 0;
}

---

2018.11.3