[学习笔记]NTT——快速数论变换

先要学会FFT[学习笔记]FFT——快速傅里叶变换

一、简介

FFT会爆精度。而且浮点数相乘常数比取模还大。

然后NTT横空出世了

虽然单位根是个好东西。但是，我们还有更好的东西

我们先选择一个模数，$const\space int\space p=998244353$

设g为p的单位根。这里就是3

那么有：$(\omega_n^1)^n = g^{p-1}=1\space mod \space p$

那么，假设$x=(\omega_n^1)$

其中一个解可以是：$x=g^{\frac{p-1}{n}}$

在模意义之下，我们不妨用$g^{\frac{p-1}{n}}$来代替$(\omega_n^1)$

因为是g原根，所以0~n-1这n个次方取值都不相同，可以求出点值表示。

$\omega_n^{-1}*\omega_n^1=1$

那么$\omega_n^{-1}=(g^{-1})^{\frac{p-1}{n}}$

op的时候，把$g^{-1}$当做底数即可。

其他和FFT相同。

#include<bits/stdc++.h>
#define reg register int
#define il inline
#define numb (ch^'0')
#define int long long
using namespace std;
typedef long long ll;
il void rd(ll &x){
    char ch;x=;bool fl=false;
    while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
    for(x=numb;isdigit(ch=getchar());x=x*+numb);
    (fl==true)&&(x=-x);
}
namespace Miracle{
const int mod=;
const int N=1e6+;
const int G=;
const int Gi=;
int qm(int x,int y){
    int ret=;
    while(y){
        if(y&) ret=(ll)ret*x%mod;
        x=(ll)x*x%mod;
        y>>=;
    }
    return ret;
}
int n,m;
int a[*N],b[*N];
int r[*N];
void NTT(int *f,int op){
    for(reg i=;i<n;++i){
        if(i<r[i]){
            swap(f[i],f[r[i]]);
        }
    }
    for(reg p=;p<=n;p<<=){
        int len=p/;
        ll tmp=qm(op==?G:Gi,(mod-)/p);
        for(reg k=;k<n;k+=p){
            ll buf=;
            for(reg l=k;l<k+len;++l){
                ll tt=(ll)buf*f[l+len]%mod;
                f[l+len]=((ll)f[l]-tt);
                if(f[l+len]<) f[l+len]+=mod;
                f[l]=((ll)f[l]+tt);
                if(f[l]>=mod) f[l]-=mod;
                buf=(ll)buf*tmp%mod;
            }
        }
    }
}
void prin(int x){
    if(x/) prin(x/);
    putchar(x%+'');
}
int main(){
    scanf("%d%d",&n,&m);
    for(reg i=;i<=n;++i){
        rd(a[i]);
    }
    for(reg i=;i<=m;++i){
        rd(b[i]);
    }
    for(m=n+m,n=;n<=m;n<<=);
    for(reg i=;i<n;++i){
        r[i]=r[i>>]>>|((i&)?n>>:);
    }
    NTT(a,);NTT(b,);
    for(reg i=;i<n;++i) b[i]=(ll)b[i]*a[i]%mod;
    NTT(b,-);
    ll inv=qm(n,mod-);
    for(reg i=;i<=m;++i){
        b[i]=(ll)b[i]*inv%mod;
        prin(b[i]);putchar(' ');
    }
    return ;
}

}
signed main(){
    Miracle::main();
    return ;
}

/*
   Author: *Miracle*
   Date: 2018/11/21 19:01:08
*/

NTT

应用大前提：

1.多项式答案的系数不要太大，否则模数乘一下会爆long long，而且必须小于模数

2.多项式的长度不要太长。n<2^23

3.多项式系数必须是正整数！！（废话）

感觉NTT还是一个很好用的东西

常数小，

而且做题的时候，经常会给定模数。FFT一脸懵逼。

如果模数是一个k*2^m+1，并且满足2^m>n（多项式次数），那么可以直接像刚才一样计算。（原根找一下）

如果不是，中国剩余定理合并。

留坑。

二、多项式求逆：

博客

推完式子之后，直接NTT做即可。

注意，

1.每次都要对位数取模，把位数限制在n以内。

2.计算长度为n的逆元的时候，必须算出来的是(n<<1)的多项式（因为H(x)*H(x)*F(x)是长度是n<<1的）

然后再砍掉n~(n<<1)-1的位数部分

可以都转化成点值表示，然后再求G(x)的点值表示。再插值

#include<bits/stdc++.h>
#define reg register int
#define il inline
#define numb (ch^'0')
using namespace std;
typedef long long ll;
il void rd(int &x){
    char ch;x=;bool fl=false;
    while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
    for(x=numb;isdigit(ch=getchar());x=x*+numb);
    (fl==true)&&(x=-x);
}
namespace Miracle{
const int N=1e5+;
const int mod=;
const int GG=;
const int Gi=;
int n,m;
int F[*N],G[*N],A[*N],B[*N],C[*N];
int r[*N];
int qm(int x,int y){
    int ret=;
    while(y){
        if(y&) ret=(ll)ret*x%mod;
        x=(ll)x*x%mod;
        y>>=;
    }
    return ret;
}
void NTT(int *f,int op,int n){
    for(reg i=;i<n;++i){
        if(i<r[i]) swap(f[i],f[r[i]]);
    }
    for(reg p=;p<=n;p<<=){
        int len=p/;
        int tmp=qm(op==?GG:Gi,(mod-)/p);
        for(reg k=;k<n;k+=p){
            int buf=;
            for(reg l=k;l<k+len;++l){
                int tt=(ll)buf*f[l+len]%mod;
                f[l+len]=(f[l]-tt+mod)%mod;
                f[l]=(f[l]+tt)%mod;
                buf=(ll)buf*tmp%mod;
            }
        }
    }
    if(op==) return;
    int inv=qm(n,mod-);
    for(reg i=;i<n;++i) f[i]=(ll)f[i]*inv%mod;
}
void wrk(int n,int *a){
    if(n==){a[]=qm(F[],mod-);return;}

    wrk(n>>,a);
    for(reg i=;i<n;++i) A[i]=F[i];//,B[i]=a[i];
    for(reg i=n;i<(n<<);++i) A[i]=;//=B[i]=0;
    for(reg i=;i<(n<<);++i){
        r[i]=r[i>>]>>|((i&)?n:);
    }

       NTT(A,,(n<<)),NTT(a,,(n<<));

    for(reg i=;i<(n<<);++i){
        a[i]=(-(ll)A[i]*a[i]%mod+mod)%mod*a[i]%mod;
    }
    NTT(a,-,(n<<));

    for(reg i=n;i<(n<<);++i) a[i]=;
}
int main(){
    scanf("%d",&n);
    for(reg i=;i<n;++i){
        rd(F[i]);C[i]=F[i];
    }
    int len;
    for(len=;len<n;len<<=);
    wrk(len,G);
    for(reg i=;i<n;++i){
        printf("%d ",G[i]);
    }
    return ;
}

}
signed main(){
    Miracle::main();
    return ;
}

/*
   Author: *Miracle*
   Date: 2018/11/21 21:49:51
*/

多项式求逆

三、多项式除法

小学/初中奥数中有一种因式分解的方法，叫做长除法。

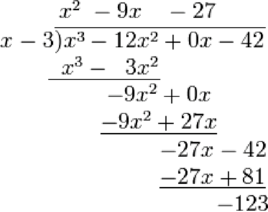
现在，我们终于可以用计算机实现了23333！！

直接那样做是O(n^2)的

但是我们有NTT和多项式求逆的工具。

具体方法是：

设$A_R(x)=x^n*A(\frac{1}{x})$

（其实发现，$A_R(x)$的系数就是$A(x)$的系数$reverse$一下）

有：

$F(x)=Q(x)*G(x)+R(x)$

$F(\frac{1}{x})=Q(\frac{1}{x})*G(\frac{1}{x})+R(\frac{1}{x})$

$x^n*F(\frac{1}{x})=x^{(n-m)}*Q(\frac{1}{x})*x^m*G(\frac{1}{x})+x^{n-m+1}*x^{m-1}*R(\frac{1}{x})$

$F_R(x)=Q_R(x)*G_R(x)+x^{n-m+1}*R_R(x)$

那么一定有：

$F_R(x)=Q_R(x)*G_R(x)\space mod \space x^{n-m+1}$

$Q_R(x)=F_R(x)*G_R^{-1}\space mod \space x^{n-m+1}$

求出$G_R$的逆元（特别注意，这里的$G_R^{-1}$的次数是$n-m$，否则可能在$n-m>m$的时候，消不成），

然后就求出了$Q_R$

由于$Q_R$一共就$n-m+1$项，所以再翻转回来，就得到了$Q_R$了。

$F(x)=Q(x)*G(x)+R(x)$

所以：

$R(x)=F(x)-Q(x)*G(x)$

如果没算错的话，$R(x)$的次数一定小于$m$的

代码：

#include<bits/stdc++.h>
#define reg register int
#define il inline
#define int long long
#define numb (ch^'0')
using namespace std;
typedef long long ll;
il void rd(ll &x){
    char ch;x=;bool fl=false;
    while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
    for(x=numb;isdigit(ch=getchar());x=x*+numb);
    (fl==true)&&(x=-x);
}
namespace Miracle{
const int N=1e5+;
const int mod=;
const ll GG=;
const ll Gi=;
int n,m;
ll F[N],G[*N],Q[*N],R[N];
ll a[*N],b[*N],c[*N],Gn[*N];
int r[*N];
ll qm(ll x,ll y){
    ll ret=;
    while(y){
        if(y&) ret=ret*x%mod;
        x=x*x%mod;
        y>>=;
    }
    return ret;
}
void NTT(ll *f,int op,int n){
    for(reg i=;i<n;++i){
        if(i<r[i]) swap(f[i],f[r[i]]);
    }

    for(reg p=;p<=n;p<<=){
        int len=p/;
        ll tmp=(op==)?qm((ll)GG,(mod-)/p):qm((ll)Gi,(mod-)/p);
        for(reg k=;k<n;k+=p){
            ll buf=;
            for(reg l=k;l<k+len;++l){
                ll tt=buf*f[l+len]%mod;
                f[l+len]=(f[l]-tt+mod)%mod;
                f[l]=(f[l]+tt)%mod;
                buf=buf*tmp%mod;
            }
        }
    }
}
void mul(ll *a,ll *b,int n,int m){//clac A*B return b
    for(m=n+m-,n=;n<m;n<<=);
    for(reg i=;i<n;++i){
        r[i]=r[i>>]>>|((i&)?n>>:);
    }
    NTT(a,,n);NTT(b,,n);
    for(reg i=;i<n;++i) b[i]=a[i]*b[i]%mod;
    NTT(b,-,n);
    ll inv=qm(n,mod-);
    for(reg i=;i<n;++i) b[i]=b[i]*inv%mod;
}
void wrk(int n,ll *a){//clac ni
    if(n==){
        a[]=qm(b[],mod-);return;
    }
    wrk(n>>,a);
    for(reg i=;i<n;++i)c[i]=b[i];
    for(reg i=n;i<(n<<);++i)c[i]=;
    for(reg i=;i<(n<<);++i){
        r[i]=r[i>>]>>|((i&)?n:);
    }
    NTT(c,,((int)n<<));
    NTT(a,,((int)n<<));
    for(reg i=;i<(n<<);++i){
        a[i]=(-(ll)a[i]*c[i]%mod+mod)%mod*a[i]%mod;
    }
    NTT(a,-,(n<<));
    ll inv=qm((n<<),mod-);
    for(reg i=;i<n;++i) a[i]=a[i]*inv%mod;
    for(reg i=n;i<(n<<);++i) a[i]=;

}

int main(){
    scanf("%lld%lld",&n,&m);
    for(reg i=;i<=n;++i) rd(F[i]),a[i]=F[i];
    for(reg i=;i<=m;++i) rd(G[i]),b[i]=G[i];
    reverse(b,b+m+);
    int len;
    for(len=;len<n-m+;len<<=);
    wrk(len,Gn);

//    cout<<" bb "<<endl;
//    for(reg i=0;i<=m;++i){
//        cout<<b[i]<<" ";
//    }cout<<endl;
//    cout<<" G-1 "<<endl;
//    for(reg i=0;i<=n-m;++i){
//        cout<<Gn[i]<<" ";
//    }cout<<endl;

    reverse(a,a+n+);
    for(reg i=n-m+;i<=n;++i) a[i]=;
    for(reg i=n-m+;i<=m;++i) Gn[i]=;
//    cout<<" FR "<<endl;
//    for(reg i=0;i<=n-m;++i){
//        cout<<a[i]<<" ";
//    }cout<<endl;
    mul(Gn,a,n-m+,n-m+);
//    cout<<" QR "<<endl;
//    for(reg i=0;i<=n-m;++i){
//        cout<<a[i]<<" ";
//    }cout<<endl;

    reverse(a,a+n-m+);

    for(reg i=;i<n-m+;++i) Q[i]=a[i],printf("%lld ",Q[i]);
    puts("");
    mul(Q,G,n-m+,m+);

    for(reg i=;i<m;++i){
        R[i]=(F[i]-G[i]+mod)%mod;
        printf("%lld ",R[i]);
    }
    return ;
}

}
signed main(){
    Miracle::main();
    return ;
}

/*
   Author: *Miracle*
   Date: 2018/11/22 17:15:16
*/

多项式除法

四、任意模数NTT

【模板】任意模数NTT

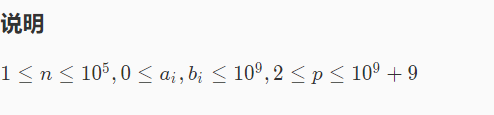
常用的解法是这样的：

答案小于10^23

取3个模数const ll m1 = 469762049, m2 = 998244353, m3 = 1004535809;

每个模数都是a*2^k+1并且k够用

m1*m2*m3>10^23

所以答案在mod m1*m2*m3下的结果就是答案

对三个质数分别做一次NTT

然后对每个系数依次用CRT合并

合并的时候，为了防止爆long long：

补充：

所有过程不涉及log^2n的快速幂快速乘，

而且最后的k*M+A一定小于m1*m2*m3,并且三个同余方程都满足

所以可以直接对p取模了。

代码：

#include<bits/stdc++.h>
#define reg register int
#define il inline
#define numb (ch^'0')
using namespace std;
typedef long long ll;
il void rd(int &x){
    char ch;x=;bool fl=false;
    while(!isdigit(ch=getchar()))(ch=='-')&&(fl=true);
    for(x=numb;isdigit(ch=getchar());x=x*+numb);
    (fl==true)&&(x=-x);
}
namespace Miracle{
const int N=2e5+;
const int G=;
const ll m1 = , m2 = , m3 = ;
int n,m,p;
ll a[*N],b[*N],f[][*N],g[*N];
ll add(ll x,ll y,ll mod){
    return x+y>=mod?x+y-mod:x+y;
}
ll qk(ll x,ll y,ll mod){
    x%=mod;y%=mod;
    ll ret=;
    while(y){
        if(y&) ret=add(ret,x,mod);
        x=add(x,x,mod);
        y>>=;
    }
    return ret;
}
ll qmo(ll x,ll y,ll mod){
    ll ret=;
    x%=mod;
    while(y){
        if(y&) ret=ret*x%mod;
        x=x*x%mod;
        y>>=;
    }
    return ret;
}
int rev[*N];
void NTT(ll *f,int n,int c,ll mod){
    ll GI=qmo(G,mod-,mod);
    for(reg i=;i<n;++i){
        if(i<rev[i]) swap(f[i],f[rev[i]]);
    }
    for(reg p=;p<=n;p<<=){
        ll gen;
        int len=p/;
        if(c==) gen=qmo(G,(mod-)/p,mod);
        else gen=qmo(GI,(mod-)/p,mod);
        for(reg l=;l<n;l+=p){
            ll buf=;
            for(reg k=l;k<l+len;++k){
                ll tmp=buf*f[k+len]%mod;
                f[k+len]=(f[k]-tmp+mod)%mod;
                f[k]=(f[k]+tmp)%mod;
                buf=buf*gen%mod;
            }
        }
    }
}
void clac(ll *f,ll *g,int n,ll mod){
    NTT(f,n,,mod);NTT(g,n,,mod);
    for(reg i=;i<n;++i) f[i]=f[i]*g[i]%mod;
    NTT(f,n,-,mod);
    ll inv=qmo(n,mod-,mod);
    for(reg i=;i<n;++i) f[i]=f[i]*inv%mod;
}
int main(){
    rd(n);rd(m);rd(p);
    for(reg i=;i<=n;++i) scanf("%lld",&a[i]),f[][i]=a[i];
    for(reg j=;j<=m;++j) scanf("%lld",&b[j]),g[j]=b[j];
    for(m=n+m,n=;n<=m;n<<=);
    for(reg i=;i<n;++i){
        rev[i]=(rev[i>>]>>)|((i&)?n>>:);
    }
    clac(f[],g,n,m1);

    for(reg i=;i<n;++i) g[i]=b[i],f[][i]=a[i];
    clac(f[],g,n,m2);
    for(reg i=;i<n;++i) g[i]=b[i],f[][i]=a[i];
    clac(f[],g,n,m3);
    for(reg i=;i<=m;++i){
        ll A=(qk(qk(f[][i],m2,m1*m2),qmo(m2,m1-,m1),m1*m2)+qk(qk(f[][i],m1,m1*m2),qmo(m1,m2-,m2),m1*m2))%(m1*m2);
    //    cout<<" AA "<<A<<endl;
        ll K=(f[][i]-A%m3+m3)%m3*qmo(m1*m2%m3,m3-,m3)%m3;
    //    cout<<" KK "<<K<<endl;
        ll op=(K*m1%p*m2%p+A%p)%p;
        printf("%lld ",op);
    }
    return ;
}

}
signed main(){
    Miracle::main();
    return ;
}

/*
   Author: *Miracle*
   Date: 2019/1/9 21:23:11
*/