【BZOJ】1656：[Usaco2006 Jan]The Grove 树木（bfs+特殊的技巧）

http://www.lydsy.com/JudgeOnline/problem.php?id=1656

神bfs！

我们知道，我们要绕这个联通的树林一圈。

那么，我们想，怎么才能让我们的bfs绕一个圈做bfs呢

我们可以这样：从联通的任意边界点引一条交边界的射线。

为什么呢？因为这样当我们的bfs到这条射线时，我们可以不向射线拓展！

可是我们考虑的是绕一个圈，那么我们要考虑从另一个放向到达射线的情况（即饶了一圈后到射线我们要考虑拓展）

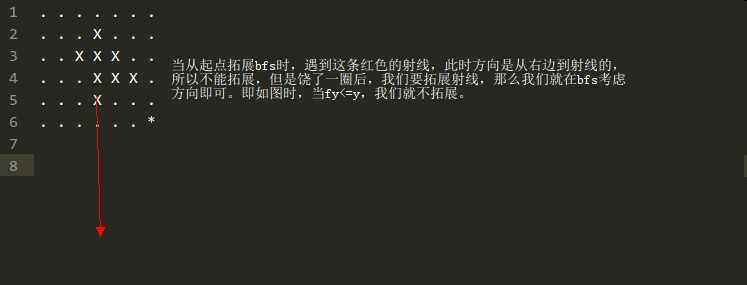
这样我们就能保证绕了联通块一圈，然后是最短距离

具体细节看代码

#include <cstdio>

#include <cstring>

#include <cmath>

#include <string>

#include <iostream>

#include <algorithm>

#include <queue>

using namespace std;

#define rep(i, n) for(int i=0; i<(n); ++i)

#define for1(i,a,n) for(int i=(a);i<=(n);++i)

#define for2(i,a,n) for(int i=(a);i<(n);++i)

#define for3(i,a,n) for(int i=(a);i>=(n);--i)

#define for4(i,a,n) for(int i=(a);i>(n);--i)

#define CC(i,a) memset(i,a,sizeof(i))

#define read(a) a=getint()

#define print(a) printf("%d", a)

#define dbg(x) cout << #x << " = " << x << endl

#define printarr2(a, b, c) for1(i, 1, b) { for1(j, 1, c) cout << a[i][j] << '\t'; cout << endl; }

#define printarr1(a, b) for1(i, 1, b) cout << a[i] << '\t'; cout << endl

inline const int getint() { int r=0, k=1; char c=getchar(); for(; c<'0'||c>'9'; c=getchar()) if(c=='-') k=-1; for(; c>='0'&&c<='9'; c=getchar()) r=r*10+c-'0'; return k*r; }

inline const int max(const int &a, const int &b) { return a>b?a:b; }

inline const int min(const int &a, const int &b) { return a<b?a:b; }

const int N=60, Q=N*N*10, dx[]={-1, 1, 0, 0, -1, 1, -1, 1}, dy[]={0, 0, -1, 1, -1, -1, 1, 1};

int a[N][N], line[N][N], f[2][N][N], n, m, front, tail, flag, x, y, X, Y;

struct dat { int x, y, f; }q[Q];

int main() {

	read(n); read(m);

	for1(i, 1, n) for1(j, 1, m) {

		char ch=getchar(); while(ch!='.'&&ch!='X'&&ch!='*') ch=getchar();

		if(ch=='X') a[i][j]=1, x=i, y=j;

		else if(ch=='*') X=i, Y=j;

	}

	for1(i, 1, n) if(i+x<=n) line[i+x][y]=1; else break;

	q[tail].x=X, q[tail].y=Y, q[tail++].f=0;

	while(front!=tail) {

		dat &t=q[front++]; if(front==Q) front=0;

		x=t.x, y=t.y, flag=t.f;

		rep(i, 8) {

			int fx=dx[i]+x, fy=dy[i]+y;

			if(fx<0 || fy<0 || fx>n || fy>m || a[fx][fy]) continue;

			if((line[x][y] || line[fx][fy]) && fy<=y) continue; //当前在射线上或下一个点是射线上时（即从右向左），不能向左拓展

			if(line[fx][fy] && !f[1][fx][fy]) { //当这是从射线左边向射线过来时，更新上的点

				f[1][fx][fy]=f[flag][x][y]+1;

				q[tail].x=fx, q[tail].y=fy, q[tail++].f=1; if(tail==Q) tail=0;

			}

			else if(!f[flag][fx][fy]) { //继承饶了一圈后的距离向四周拓展

				f[flag][fx][fy]=f[flag][x][y]+1;

				q[tail].x=fx, q[tail].y=fy, q[tail++].f=flag; if(tail==Q) tail=0;

			}

		}

	}

	print(f[1][X][Y]);

	return 0;

}

Description

The pasture contains a small, contiguous grove of trees that has no 'holes' in the middle of the it. Bessie wonders: how far is it to walk around that grove and get back to my starting position? She's just sure there is a way to do it by going from her start location to successive locations by walking horizontally, vertically, or diagonally and counting each move as a single step. Just looking at it, she doesn't think you could pass 'through' the grove on a tricky diagonal. Your job is to calculate the minimum number of steps she must take. Happily, Bessie lives on a simple world where the pasture is represented by a grid with R rows and C columns (1 <= R <= 50, 1 <= C <= 50). Here's a typical example where '.' is pasture (which Bessie may traverse), 'X' is the grove of trees, '*' represents Bessie's start and end position, and '+' marks one shortest path she can walk to circumnavigate the grove (i.e., the answer): ...+... ..+X+.. .+XXX+. ..+XXX+ ..+X..+ ...+++* The path shown is not the only possible shortest path; Bessie might have taken a diagonal step from her start position and achieved a similar length solution. Bessie is happy that she's starting 'outside' the grove instead of in a sort of 'harbor' that could complicate finding the best path.

牧场里有一片树林，林子里没有坑．

贝茜很想知道，最少需要多少步能围绕树林走一圈，最后回到起点．她能上下左右走，也能走对角线格子．牧场被分成R行C列 (1≤R≤50，1≤C≤50)．下面是一张样例的地图，其中“．”表示贝茜可以走的空地， “X”表示树林， “*”表示起点．而贝茜走的最近的路已经特别地用“+”表示出来．

题目保证，最短的路径一定可以找到．

Input

* Line 1: Two space-separated integers: R and C

* Lines 2..R+1: Line i+1 describes row i with C characters (with no spaces between them).

第1行输入R和C，接下来R行C列表示一张地图．地图中的符号如题干所述．

Output

* Line 1: The single line contains a single integer which is the smallest number of steps required to circumnavigate the grove.

输出最少的步数．

Sample Input

6 7
.......
...X...
..XXX..
...XXX.
...X...
......*

Sample Output