函数导出在kvm_intel.ko,kvm.ko不共享

KVM一共包含了三个内核模块，kvm_intel.ko，kvm_amd.ko，kvm.ko。其中两个重要文件x86.c和vmx.c在编译后分别会生成kvm_intel.ko和kvm.ko两个内核模块，所以在两个文件当中定义的同一个结构体，在另一个文件中不能共用，因为两者处于不同内核模块。举例说明
在kvm_host.h中定义结构体数组如下：

#define table_len 10000
struct vm_task_table
{
    unsigned long vm_task_cr3;
    pid_t vm_task_pid;
    char vm_task_name[];
}vm_table[table_len];

现在想在x86.c和vmx.c中共用该结构体，一个向结构体数组写入值，一个读出值。定义如下：
x86.c
extern struct vm_task_table vm_table[table_len];
vmx.c
extern struct vm_task_table vm_table[table_len];

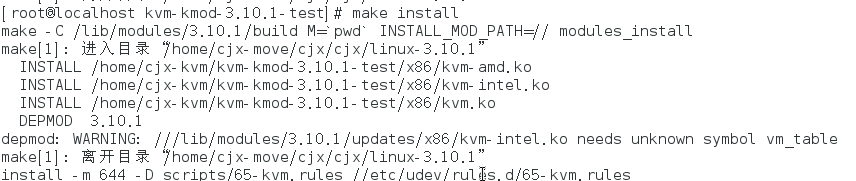
首先且不说两个文件的结构体是否是同一个的问题。在编译过程中，将会报错如下：

因为kvm_host.h中直接定义了vm_table变量，而在kvm其他文件中，只要包含了kvm_host.h文件，编译器在编译过程中都会判断出当前变量被重复定义。首先要编译不出错，vm_table变量不能在kvm_host,h中声明，修改代码为：

kvm_host.h

#define table_len 10000
struct vm_task_table
{
    unsigned long vm_task_cr3;
    pid_t vm_task_pid;
    char vm_task_name[];
};

x86.c

struct vm_task_table vm_table[table_len]

vmx.c

extern struct vm_task_table vm_table[table_len]

此时编译过程中将不会出错，但在make install中会有如下警告

提示kvm_intel.ko模块不能识别vm_table符号。原因是，x86.c和vmx.c文件生成不同的内核模块，两者之间信息不共享，采用extern的方法不能够引用vm_table变量。

所以，正确的方法应为：

kvm_host.h

#define table_len 10000
struct vm_task_table
{
    unsigned long vm_task_cr3;
    pid_t vm_task_pid;
    char vm_task_name[];
};

x86.c

struct vm_task_table vm_table[table_len]；

EXPORT_SYMBOL_GPL(vm_table);

vmx.c

extern struct vm_task_table vm_table[table_len]

将vm_table符号导出到内核符号表，其他内核模块则可以进行引用。得到正确结果。