POJ 2057 The Lost House

题意：一只蜗牛，它的房子在树上的某个叶子节点上，它要从树的根节点出发，寻找自己的房子。树的任意两个节点的距离为1，房子出现在每个叶子节点上的可能性一样。有的节点上有虫子，如果有虫子，虫子会告诉蜗牛它的房子是不是在这个节点为根的子树上。求蜗牛所走距离的最小期望。

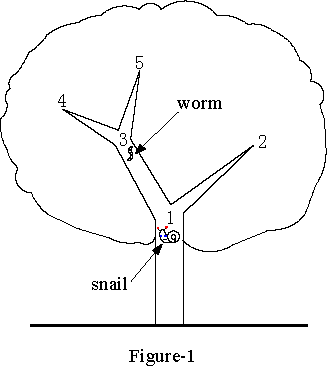
　　　如下图，如果蜗牛制定的策略先到2，再到5再到4，则由于房子地点的不确定，所以可能走的距离为1,4,6，所以期望为11/3。如果制定的策略是先到3,根据虫子的话判断去4和5还是去2，则可能走的距离为2,4,3，所以期望为9/3 = 3。可以证明，最小的期望即为3。

解法：首先，设叶子节点总数为tt，则肯定会有tt种情况，所以只需要求出所有情况下，找到房子所需要走的距离之和即可。

　　　设le[x]表示以x为根的子树上叶子节点的个数；

　　　设su[x]表示在以x为根的子树上，各种情况下找到房子所需走的距离之和；（0为根节点，su[0] / le[0]即为所求）

　　　设fail[x]表示在以x为根的子树上，遍历整个子树没有找到房子又返回x节点所需要走的距离和。

　　　则le[x] += le[v[i]]，v是x的子节点集合；

　　　for (int i = 0; i < v.size(); ++ i) { su[x] += (fail[x] + 1) * le[y] + su[y]；fail[x] += fail[y] + 2;}（这个状态转移方程很精妙，多体会下，最好画个树手算模拟一下）

tag:树形dp, think, good

 /*
  * Author:  Plumrain
  * Created Time:  2013-11-20 10:39
  * File Name: (good)DP-POJ-2057.cpp
  */
 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <algorithm>
 #include <vector>

 using namespace std;

 #define CLR(x) memset(x, 0, sizeof(x))
 #define PB push_back

 int n;
 bool w[];
 vector<int> v[];
 int le[], fail[], su[];

 bool cmp(int x, int y)
 {
     return (fail[x]+)*le[y] < (fail[y]+)*le[x];
 }

 void init()
 {
     CLR (le); CLR (fail); CLR (su); CLR (w);
     for (int i = ; i < n; ++ i)
         v[i].clear();

     int t1;
     char s[];
     for (int i = ; i < n; ++ i){
         scanf ("%d%s", &t1, s);
         if (s[] == 'Y') w[i] = ;
         if (t1 != -) v[t1-].PB(i);
     }
 }

 void dfs(int x)
 {
     if (!v[x].size()){
         le[x] = ;
         su[x] = ;
         fail[x] = ;
         return;
     }

     for (int i = ; i < (int)v[x].size(); ++ i){
         dfs(v[x][i]);
         le[x] += le[v[x][i]];
     }

     sort (v[x].begin(), v[x].end(), cmp);
     for (int i = ; i < (int)v[x].size(); ++ i){
         int y = v[x][i];
         su[x] += (fail[x]+)*le[y] + su[y];
         fail[x] += fail[y] + ;
     }
     if (w[x]) fail[x] = ;
 }

 int main()
 {
     while (scanf("%d", &n) != EOF && n){
         init();
         dfs();
         printf ("%.4f\n", (double)su[] / le[]);
     }
     return ;
 }